CS231n 강의 정리 (1~7강)

스탠포드 대학교의 CS231n 강의를 듣고 요약, 필기한 글입니다.

1. Introduction

인터넷과 이미지 매체의 발전, ImageNet과 같은 거대 데이터셋의 구축, 빠르게 늘어난 컴퓨터의 연산 능력과 GPU의 성능은 딥러닝과 컴퓨터 비전의 발전에 크게 기여하였다.

컴퓨터 비전 분야는 그동안 많은 진보를 거쳤고 지금도 빠르게 발전하고 있는 분야지만, 이미지에서 서로 다른 객체 간의 관계를 파악한다거나, 배경지식을 통해 숨어있는 맥락을 읽어낸다거나... 등등 아직 더 가야 할 길이 한참 남아있는 분야이기도 하다.

2. Image Classification

컴퓨터가 인간처럼 이미지를 인식하고 분류하기 위해서는 수많은 어려움을 극복해야 한다.

• 똑같은 객체여도 사진의 구도나 조명이 바뀌거나, 다른 물체에 일부가 가려지거나, 배경과 비슷해 보이는 이미지가 있을 수 있음. 우리의 알고리즘은 이런 상황에 대한 '강인함'이 필요함.

• Semantic Gap: 컴퓨터에게 이미지는 인간과 달리 '수많은 숫자들의 집합'으로 보일 뿐임. 이미지의 형태가 조금만 달라지더라도 실제로는 수많은 픽셀 값들이 변동됨.

이미지를 인식하는 알고리즘을 만들기 위해서 다음 방법을 떠올릴 수 있다.

• 명시적인 규칙 집합 만들기: 객체를 설명하는 규칙들을 직접 작성함. 예를 들어 숫자 '2'는 '이미지 상단에 위로 볼록한 곡선이 있고, 하단에는 수평선이 있고, ...'
  • 그러나 이는 강인하지 않으며 (즉, 미세한 변동에도 쉽게 영향을 받으며) 객체마다 매번 상응하는 규칙이 필요하므로 확장성이 없음.

• 데이터 중심 접근법(Data-driven approach): 먼저 수많은 데이터를 수집한 후 'Machine Learning Classifier'를 학습시켜 새로운 데이터에 대한 분류를 예측하도록 함.
  • 이미지와 레이블을 받아 모델을 출력하는 Train 함수와, 그 모델로부터 예측 결과를 출력하는 Predict 함수로 구성됨.

KNN 알고리즘

CIFAR-10: 10가지 카테고리와 50,000여 개의 학습용 이미지, 10,000여 개의 테스트 이미지로 이루어진 거대한 이미지 데이터셋.

• 각 이미지는 32×32 픽셀의 3채널 컬러 이미지임. (32×32×3, 즉 3차원 데이터)

Nearest Neighbor(NN) 알고리즘: 훈련 단계에서는 모든 학습 데이터를 기억하고, 예측 단계에서는 새로운 이미지가 들어오면 기존 학습 데이터를 비교해서 '가장 비슷한 이미지'로 레이블을 예측함.

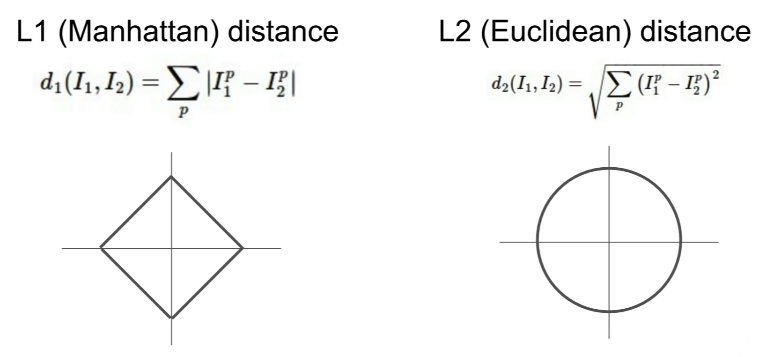
• 정확히는 시험 이미지와 훈련 이미지의 각 픽셀마다 값의 차이를 계산하고 절댓값을 씌운 뒤 총합을 구함. (= L1 Distance)
• 훈련 단계에선 단순 기억만 하므로 O(1), 예측 단계에선 기억한 모든 데이터와 비교를 거쳐야 하므로 O(N)의 시간이 걸림. ⇒ 보통은 훈련이 느리고 시험이 빠른 것이 좋음... (반대!)

K-Nearest Neighbor(KNN) 알고리즘: NN 알고리즘의 개선 버전. 거리 척도를 통해 가까운 이웃을 K개 찾고, 이웃끼리 투표를 해서 가장 많은 득표수를 획득한 레이블로 예측함.

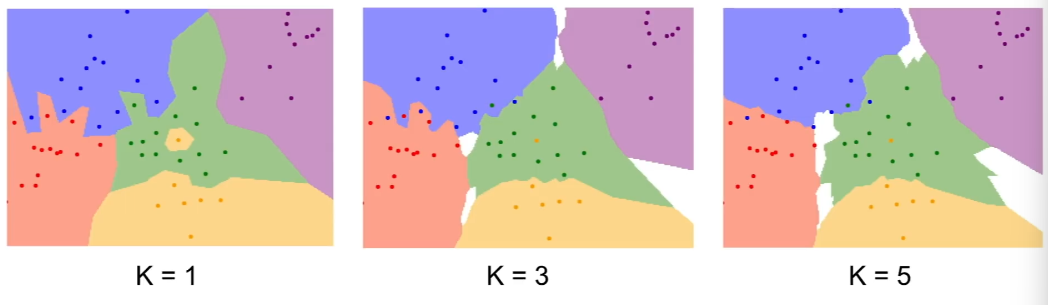
위 이미지를 보면 K 값이 높아질수록 분류 경계가 부드러워지고, 동떨어져 있던 예측값도 자연스럽게 주변의 분류로 흡수되는 것을 알 수 있다.

• 단, 이미지를 다룰 때 KNN은 별로 좋은 방법이 아니라고 함.
• 어떤 거리 척도를 사용하느냐에 따라 다룰 수 있는 데이터가 달라짐.
  • L2 distance: '제곱 합의 제곱근'을 거리로 이용. L1과 달리 좌표계의 영향을 받지 않음.

💡 L1과 L2 중 어떤 것을 '거리 척도'로 선택해야 할까?

• 문제와 데이터의 성질에 따라 달라짐. 직접 시도해 보고 더 좋은 것을 택하자!
• 강의에서는 특징 벡터 각각의 요소들이 자체적인 의미를 갖고 있을 때 L1 distance가 좀 더 어울린다는 식으로 설명됨.

하이퍼파라미터 선택

K 값과 거리 척도처럼 학습을 통해서 얻어지지 않고 사람이 직접 지정해야 하는 매개변수를 '하이퍼파라미터'라고 한다. 그럼 어떻게 하이퍼파라미터를 선택해야 할까?

1. '훈련 데이터'의 정확도와 성능을 최대화하는 것을 선택
   ⇒ 안 좋음! 실제 데이터를 잘 분류하는 것이 더 중요함.

2. 데이터를 '훈련 데이터'와 '시험 데이터'로 나누고, 시험 데이터에서 가장 최적의 결과를 내는 것을 선택
   ⇒ 역시 안 좋음! 시험 데이터에 대해서만 잘 동작하는 하이퍼파라미터를 고른 것일 수 있음.

3. 데이터를 '훈련', '검증', '시험' 데이터 3가지로 나누고, 검증 데이터에 대해 가장 좋았던 분류기를 가지고 시험 데이터를 통해 성능을 평가
   ⇒ ✅ 가장 일반적. 시험 데이터는 모델을 완성한 후 '오직 한 번만' 사용해야 함.

4. Cross-Validation: 먼저 시험 데이터를 정해놓고, 나머지 데이터를 여러 부분으로 나눈 후 그중에서 검증 데이터를 번갈아가면서 지정함. 실제 딥러닝에선 잘 쓰이지 않음.

실제 이미지 분류에는 K-NN 분류기를 쓰지 않는다. 일단 너무 느리고, L1/L2 거리 척도가 이미지 간의 '지각적 유사도'를 측정하기에 적절하지 않기 때문이다.

💡 '차원의 저주'란?

⇒ 차원이 증가할수록 모든 공간을 조밀하게 채우기 위해 필요한 데이터가 기하급수적으로 늘어나는 현상을 말한다. N차원에서의 부피를 생각하면 된다.

Linear Classification

선형 분류자는 신경망을 이루는 가장 기본적인 블록 역할을 한다. 'Parametric Model'의 가장 단순한 형태이기도 하다.

• Parametric Model: 학습을 통해 결정해야 하는 파라미터의 수가 유한한 모델.

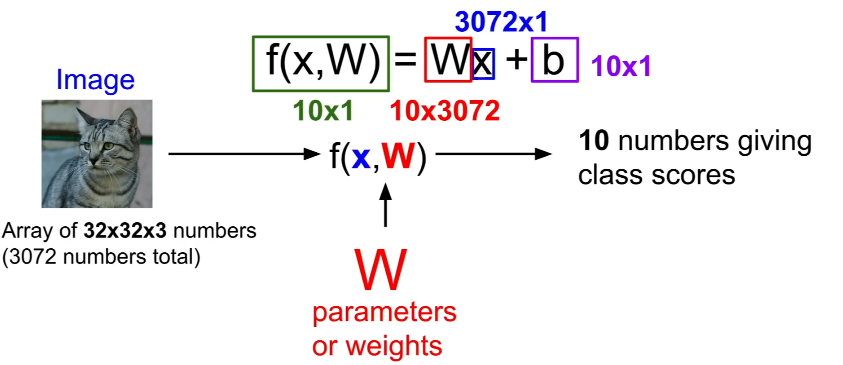
위 그림의 예시에서 $f$는 입력 이미지 $x$와 파라미터(가중치) $W$를 받아 10개의 숫자(카테고리별 점수)를 출력한다.

• 훈련 데이터의 정보를 요약하여 파라미터 W에 모아주므로 시험 단계에서 훈련 데이터가 필요하지 않음.
• 수식으로는 $F(x, W) = Wx + b$로 나타낼 수 있음.
  • 이때 각 요소는 행렬 또는 벡터이므로 연산 시 차원(형상)이 중요함.
  • 가령, 입력 이미지는 32×32 픽셀의 3채널 이미지이므로, 이를 길게 펴서 열 벡터로 만들면 3072차원의 벡터가 됨.
  • 이때 $b$는 편향(bias)으로, '데이터와 무관하게' 특정 분류에 '우선권'을 부여하는 역할을 함.

2×2 크기의 단일 채널 이미지를 받아 3가지 분류 중 하나로 분류하는 간단한 예시를 들면 이런 식으로 연산이 이루어진다.

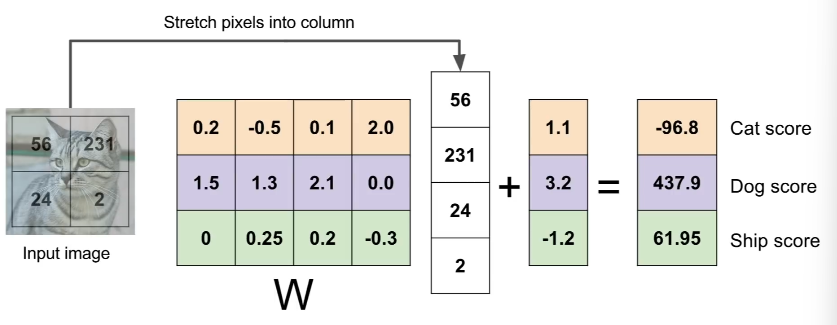
한편, 아래 그림은 학습을 마친 가중치 행렬 $W$를 시각화한 것이다. 각 분류에 해당하는 입력 이미지와 연산되었을 때 자신의 점수를 최대로 만드는 값으로 수렴한 것이라 보면 될 것 같다.

• 선형 분류의 문제는 각 분류에 대해서 하나의 템플릿만 학습하게 된다는 점임. (모든 것을 '평균화' 시키므로)

• 각 이미지를 고차원 공간의 한 점이라 생각한다면 선형 분류자는 각 클래스를 구분시켜 주는 '선형 결정 경계'를 그어주는 역할을 함. 즉, 직선 하나로 분류할 수 없는 문제라면 선형 분류를 통해 풀기 힘듦.
  • Multimodal Data: 한 클래스가 다양한 공간에 분포할 수 있는 데이터.

3. Loss Functions and Optimization

손실 함수는 예측 함수와 문제의 정답을 입력으로 받아서 현재 가중치가 '얼마나 잘못 예측하는지'를 정량적으로 알려주는 함수이다.

• 수식: $L = \frac{1}{N}\sum_{i}L_{i}(f(x_{i}, W), y_{i})$
  • 이때 $L_{i}$는 $i$번째 입력에 대한 손실이며, 전체 손실 $L$은 이를 모든 데이터에 대해 평균 낸 것.

Multi-class SVM

여러 분류를 다루기 위한 '이진 SVM'의 일반화된 형태이다.

💡 SVM이란?

서포트 벡터 머신(Support Vector Machine)으로, 두 분류 중 주어진 데이터가 어디에 속하는지 결정하는 '이진 선형 분류' 모델이다. 데이터가 존재하는 공간에서 가장 큰 폭을 갖는 경계를 찾는 것이 목표다. (참고 게시글)

• 수식: $L_{i} = \sum_{j≠y_{i}}\max(0, s_{j} - s_{y_{i}} + 1)$
  • $s$는 분류기의 출력으로 나온 예측된 점수, $y_{i}$는 이미지의 실제 정답 카테고리 번호.
  • $+1$은 'Safety Margin'으로, 정답 카테고리를 '충분히' 높게 예측했는지의 기준을 정함.

위 수식에 따르면 각 데이터마다 '정답이 아닌 분류로 예측한 점수'에서 '올바른 분류로 예측한 점수'를 빼주고 있으며, 이 값은 '정답 점수가 오답 점수보다 더 커질 때' 음수가 된다. 해당 값에 마진을 더한 값과 0 중에서 더 큰 값을 손실로 두는 것이다.

• 그래프는 정답 카테고리의 점수가 올라갈수록 선형적으로 0까지 감소하는 형태임. (= Hinge Loss)

• 처음 학습을 시작할 때 행렬 W는 임의의 작은 수들로 초기화되므로 결과 점수들이 임의의 일정한 값을 갖게 됨. 즉, 모든 점수가 0에 가깝고 값이 서로 비슷하다면 마진 * (클래스의 수 - 1)만큼의 손실이 나옴.

• 오차를 구할 때 제곱을 사용하면 '나쁜 것을 곱절로 나쁘게' 보는 것이 됨. 즉, '조금 잘못된 것'과 '많이 잘못된 것'의 차이를 강조하고 싶을 때 사용.

Regularization

학습의 궁극적인 목적은 훈련 데이터가 아닌 시험 데이터에 대한 최적의 성능을 갖게 만드는 것이며, 만약 훈련 데이터에만 '꼭 맞게(fit)' 학습시킨다면 실질적인 성능은 떨어질 수 있다.

이를 방지하는 기법이 바로 'Regularization'이다.

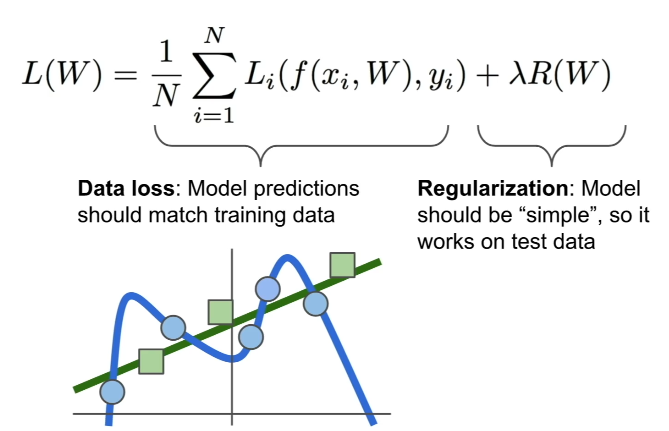
Regularization은 손실 함수에 일종의 '페널티' 역할을 하는 $λR(W)$ 항을 추가하여 모델이 좀 더 '단순한' $W$를 선택하도록 돕는다.

• $λ$는 두 항 간의 트레이드-오프 역할을 하는 하이퍼파라미터.
• $R(W)$를 정의하는 데에는 다양한 방법이 있으며, 어떻게 정의하냐에 따라 '복잡도'를 측정하는 방법이 달라짐.
  • 가령, L1은 W에서 0이 아닌 요소들의 개수가 적을수록, L2는 전체 요소가 고르게 퍼져있을수록 '덜 복잡하다'고 판단함.

Softmax Loss

소프트맥스는 딥러닝에서 주로 사용하는 손실 함수로, 점수 자체에 추가적인 의미를 부여한다.

• 수식: $L_{i} = -\log(\frac{e^{s_{y}}}{\sum_{j}e^{s_{j}}})$
• 로그 안의 값은 '정답 클래스의 확률'이 되며, 0에서 1 사이의 값을 가지고 총합은 1이 됨.
• $-\log$를 취함으로써 예측 결과가 좋을수록 (즉, 확률이 1에 가까워질수록) +0에 가까워짐.

• 학습 초기에 분류가 $C$개이고 각 점수들이 모두 0에 가까운 작은 수라면 소프트맥스 값은 $-\log(1/C) = \log C$가 됨. (디버깅에 사용됨)

• SVM에서는 정답인 점수와 정답이 아닌 점수 간의 '마진'을 신경 쓴 반면, 소프트맥스에서는 정답인 분류의 '확률'을 구해서 그 로그 값에 신경을 씀.
  • 즉, SVM은 일정 선(마진)을 넘기만 하면 더 이상 성능 개선에 신경 쓰지 않지만, 소프트맥스는 확률을 최대한 1에 가깝게 만들기 위해 성능을 끊임없이 높이려 한다는 성향의 차이가 있음.

Optimization

'어떻게 하면 손실을 최소화하는 가중치 W를 찾을 수 있을까?'
이는 지도가 없는 매우 복잡한 산맥에서 가장 밑바닥의 낮은 곳을 찾는 일과 같다.

• 임의 탐색: 임의로 샘플링한 W들을 엄청 많이 모아놓고 손실을 계산해서 어떤 W가 좋은지를 살펴보는 것. '매우 나쁘지만 가능은 하다...'

그 대신, 현재 위치에서 '기울어진' 방향을 찾아 조금씩 이동하는 것을 반복한다면 가장 낮은 곳에 도달할 수 있지 않을까?

• Gradient(그래디언트): 다변수 함수의 모든 입력값에서 모든 방향으로의 순간변화율(기울기). 벡터의 각 요소에 대한 편도함수들의 벡터.

그래디언트의 방향은 함숫값을 가장 많이 증가시키는 방향이므로, 내려갈 때는 그 반대 방향을 사용하면 될 것이다.
그래디언트를 구하는 방법은 다음 두 가지로 나뉜다.

• 유한차분법: W의 각 요소를 살짝 변화시켰을 때 발생하는 손실 값의 차이를 통해 그래디언트를 구함.
  • ⇒ 매우 오래 걸림! (하지만 파라미터 수를 어느 정도 조정하면 디버깅에 쓸 수 있음)

• Gradient Descent(경사하강법): 우선 W를 임의의 값으로 초기화한 후, 손실 값과 그래디언트를 계산한 뒤 가중치를 그래디언트의 반대 방향으로 일정 거리만큼 업데이트함.
  • Learning Rate(학습률): 그래디언트의 반대 방향으로 '얼마만큼 나아가야 할지'를 결정하는 하이퍼파라미터.

한편, 전체 손실은 각 훈련 데이터셋에 대한 손실의 평균으로 정의되는데, 만약 데이터 수가 매우 많아진다면 그만큼 작업 시간이 크게 늘어나며, 그래디언트를 구할 때에도 매번 손실 값이 필요하므로 문제가 생길 것이다.

• Stochastic Gradient Descent(SGD, 확률적 경사하강법): 따라서 전체 데이터셋이 아닌 미니배치라는 작은 데이터 집합을 만들어 사용함. 전체 손실의 '추정치'와 실제 그래디언트의 '추정치'를 계산하여 사용하는 것!
  • 미니배치의 크기는 보통 2의 승수로 정함. (32, 64, 128 등)

Image Features

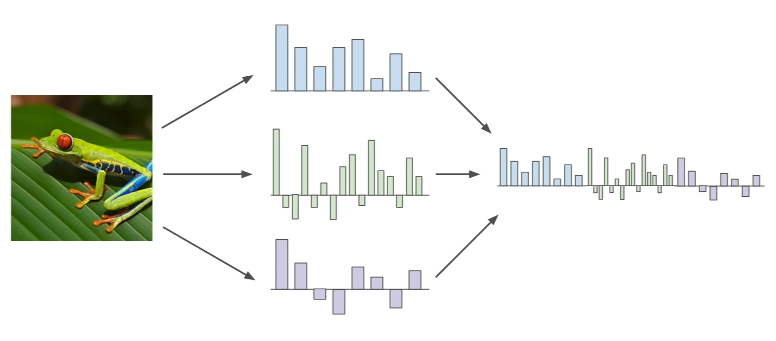
DNN(심층 신경망) 이전에는 이미지의 특징 표현들을 계산한 후 한데 모아 연결시켜(concat) 하나의 특징 벡터로 만들고, 그것을 선형 분류자의 입력으로 사용했었다.

원래는 선형으로 분류할 수 없었던 특징들을 적절한 변환을 통해 선형 분류가 가능하게끔 만드는 것이다.

강의에서 소개된 여러 특징 변환의 예는 다음과 같다.

• 컬러 히스토그램: 이미지에서 색조 값만 뽑아서 모든 픽셀을 각 양동이에 넣는 것. 가장 간단한 특징 벡터 중 하나.
• 경사지향 히스토그램(HoG): 이미지를 작은 크기 단위(8×8 픽셀 등)로 나눈 후, 그 안에서 가장 지배적인 에지의 방향을 계산하고 그 방향을 양자화해서 양동이에 넣어 히스토그램을 계산함.
• Bag of Words: 문장을 구성하는 단어의 발생 빈도를 특징 벡터로 사용하는 자연어처리 기법에서 영감을 얻음.
  • 수많은 이미지들을 임의로 조각내어 각 조각들을 K-means와 같은 알고리즘으로 군집화함. (⇒ '시각 단어')
  • 이렇게 만들어진 시각 단어들은 여러 색깔과 다양한 방향의 에지들을 포착할 수 있음.

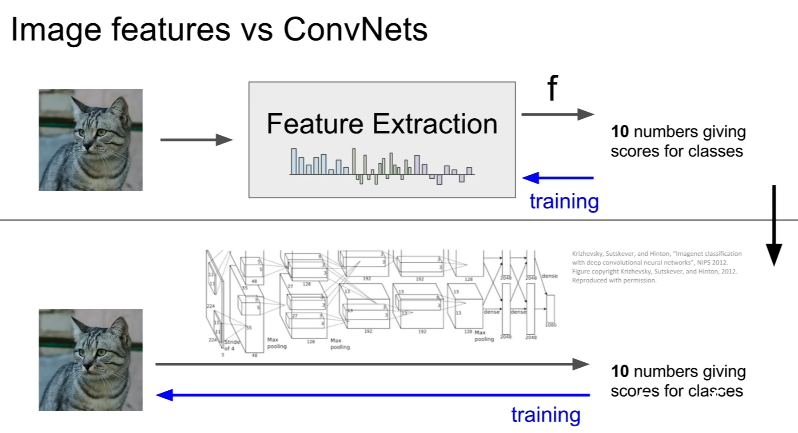
하지만 CNN과 DNN은 이렇게 '이미 만들어 놓은 특징들'을 사용하는 대신, 데이터로부터 직접 특징들을 학습하려 한다는 것이 가장 큰 차이점이다.

4. Backpropagation and Neural Network

Computational Graph(계산 그래프)는 함수의 연산 과정을 노드와 에지를 갖는 그래프 형태로 나타낸 것으로, Backpropagation(역전파)라는 기술을 사용할 수 있게 해준다.

역전파를 계산하는 방법은 다음과 같다.

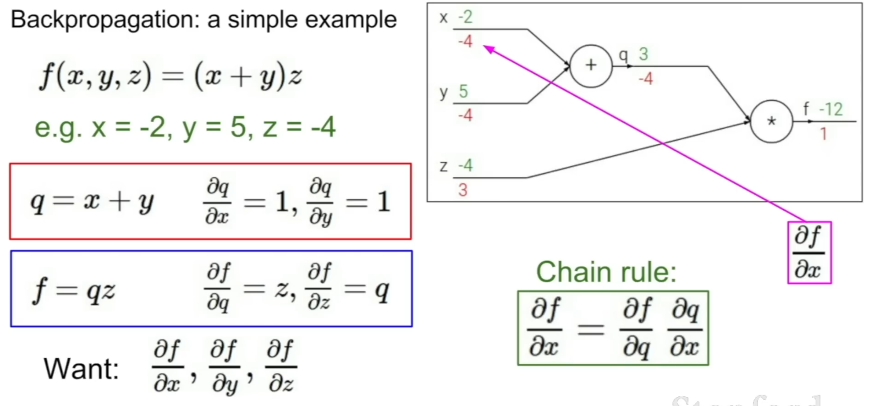
각 노드마다 자신의 '입력에 대한 출력의 미분(= Local Gradient)'을 계산한 뒤, 가장 끝에서부터 거슬러 올라가며 노드별 미분들을 곱해나간다.

• 이는 정확히 연쇄 법칙의 원리와 같음! 이를 통해 출력에 대한 모든 노드의 '영향력'을 알 수 있게 된다.
• 덧셈 노드와 곱셈 노드는 가장 기본적인 연산이므로 동작 방식을 기억해 두자.
  • 덧셈은 그대로 흘리고(Gradient Distributor), 곱셈은 바꿔서 곱하고(Gradient Switcher)

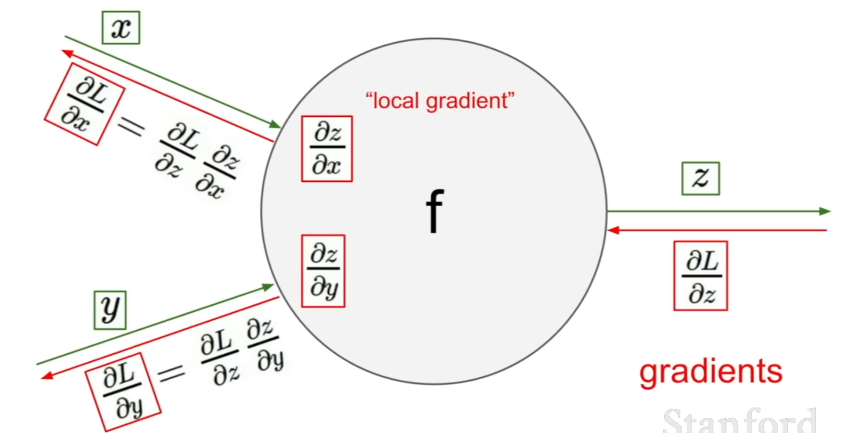
이러한 '국소적 미분'을 이용하면 아무리 복잡한 수식의 함수라도 덧셈, 곱셈, 상수배, 역수, 지수 등의 기초적인 연산 노드들로 분해하여 차근차근 그래디언트들을 계산할 수 있다.

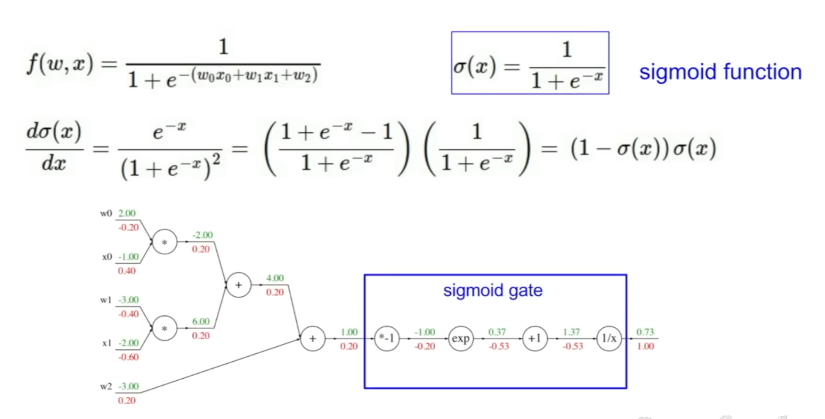
• 어떤 노드의 출력 에지가 n개라면, 순전파 때 n개의 연결된 노드들에 영향을 미치는 것이므로, 역전파 때는 반대로 n개의 그래디언트가 합해져야(덧셈) 함.

Gradients for Vector

만약 입력이 스칼라값이 아닌 벡터라면 어떻게 될까?
거의 비슷하지만 그래디언트가 Jacobian 행렬이 된다는 점이 다르다.

• Jacobian 행렬: 입력 벡터의 모든 원소에 대해 출력 벡터의 모든 원소를 미분한 값들로 이루어진 행렬.
  
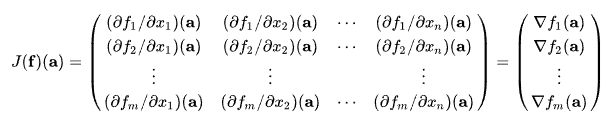
  • 그 크기는 입력 벡터의 차원과 출력 벡터의 차원이 곱해진 것이므로 (게다가 배치까지 추가된다면) 매우 커지므로 실제 계산하기 어려움.
    
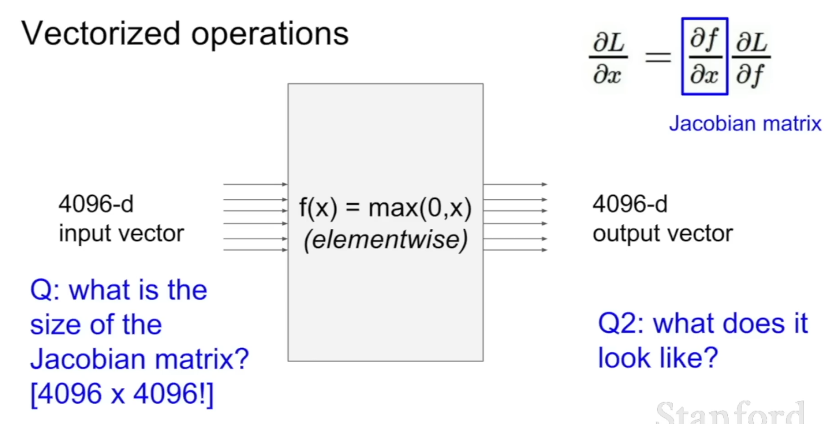
  • 하지만 만약 노드가 위와 같은 함수(f(x) = max(0, x))라면, 입력 벡터의 각 요소는 오직 출력 벡터에서 자신과 같은 위치의 요소에만 영향을 미치므로, 편미분 시 그 외 원소들은 0이 되어 대각 행렬의 형태가 될 것임. (즉, 실제 Jacobian 행렬을 작성하고 공식화할 필요 없음)
  • Jacobian 행렬에 대한 더 자세한 이해는 이 포스팅을 참고하자.

참고로 벡터의 그래디언트는 항상 원본 벡터의 크기와 동일하며, 그래디언트의 각 요소는 함수의 최종 출력에 얼마만큼의 영향을 미치는지를 의미한다.

구체적인 예시를 보면서 과정을 이해해 보자.

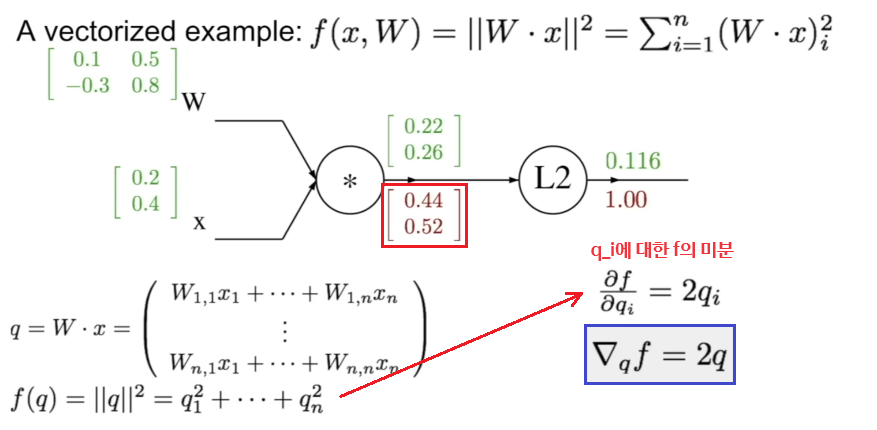
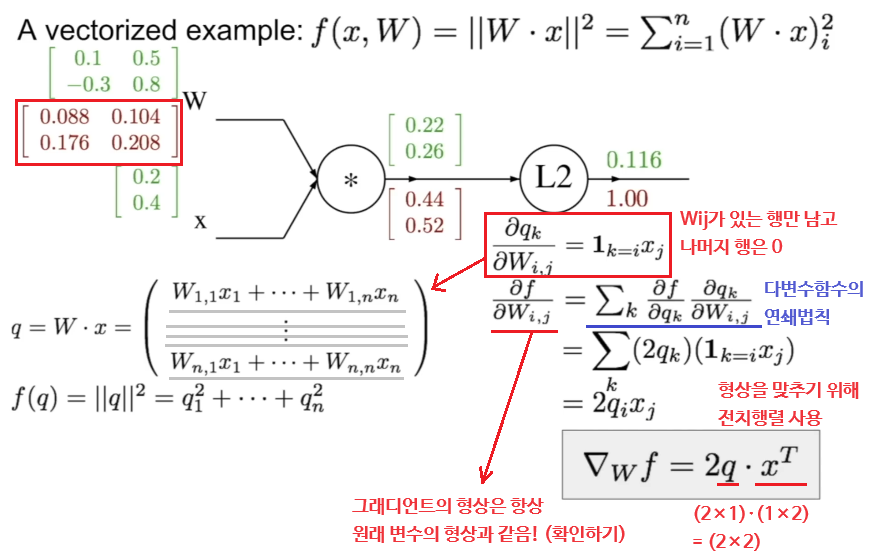
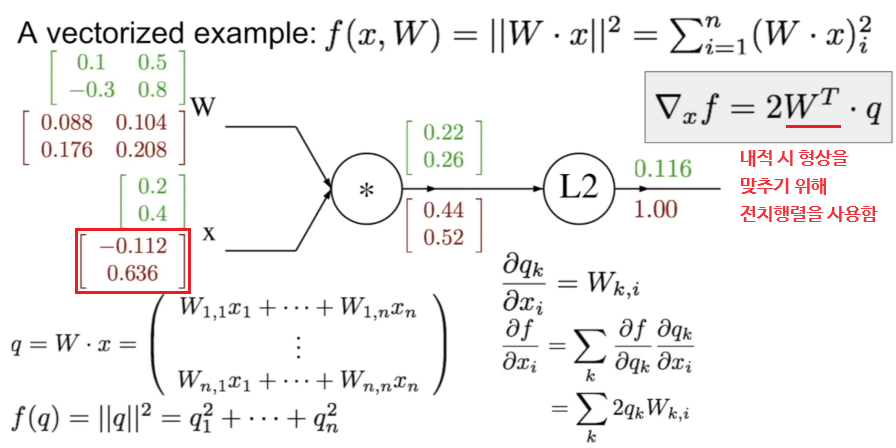
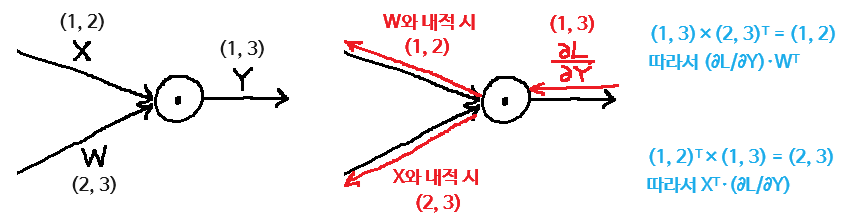
📌 행렬 내적(Affine 계층)의 역전파

수식으로 요약하면 이렇다: $Y = X·W$일 때, $\frac{∂L}{∂X} = \frac{∂L}{∂Y}·W^{T}$이고 $\frac{∂L}{∂W} = X^{T}·\frac{∂L}{∂Y}$

• 전치 행렬의 존재와 내적의 순서 때문에 다소 복잡해 보일 수 있지만, 내적 역시 일종의 '곱연산'이라 생각하면 곱셈 노드가 상류의 역전파에 '순전파 때의 반대편의 입력'을 곱하여 흘려보낸다는 점과 유사함을 느낄 수 있다.
• 여기에 '그래디언트의 형상은 원래 입력과 동일하다'는 사실을 추가로 고려하면, 상류의 역전파에 반대편의 입력을 어떻게 내적해야 원래 입력과 동일한 형상을 갖게 될지를 떠올리면서 자연스럽게 식을 유도할 수 있다.
  

실제 코드로 신경망을 구현할 때는 각 노드(게이트)를 forward(), backward() 메서드를 가진 클래스로 정의하여 모듈화한다. 그리고 여러 게이트의 게이트들을 순차적으로 호출하면서 순전파를 계산하고, 다시 역순으로 호출하면서 역전파를 계산하게 한다.

이때 순전파 때의 값을 게이트 내부에 저장(캐싱)하여, 역전파 계산 시 사용할 수 있게 하자.

Neural Network

신경망은 함수들의 집합으로, 비선형의 복잡한 함수를 만들기 위해서 간단한 함수들을 계층적으로 여러 개 쌓아올린 집합이다.

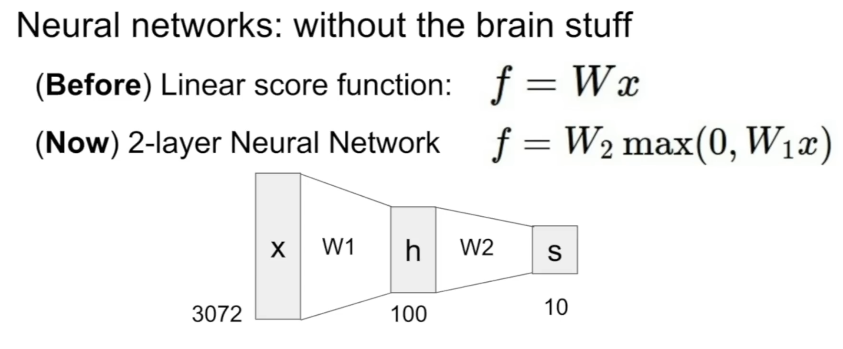
위 그림은 가장 간단한 형태의 2계층 신경망을 나타낸 것이며, max()가 비선형성을 추가하는 역할을 한다.

은닉층이 추가됨으로써 선형 분류자와 달리 하나의 클래스에 대해 여러 중간 단계의 템플릿을 학습할 수 있고, 따라서 더 다양한 특징들을 잡아낼 수 있게 되어 성능이 높아진다. (⇒ mode 문제 해결!)

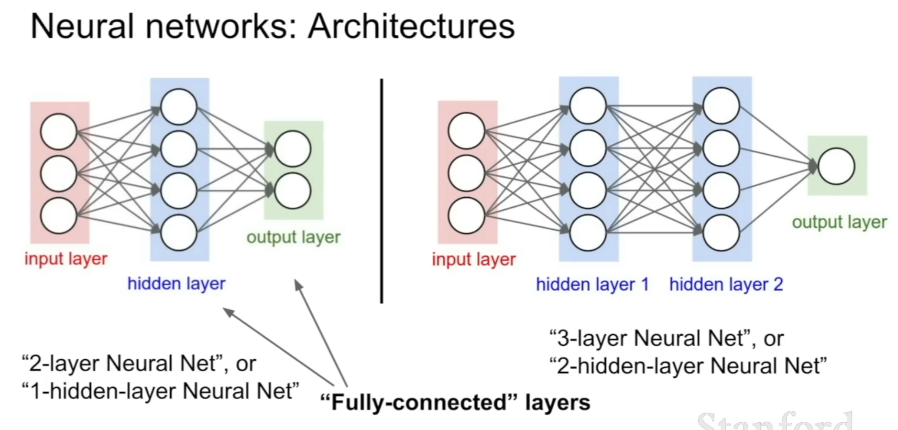
5. Convolutional Neural Network (CNN)

Fully Connected Layer(완전 연결 계층): 입력 데이터를 받아 길게 펴서 벡터로 만든 후, 가중치 행렬과 내적한 결과를 출력함.

Convolution Layer(합성곱 계층): 완전 연결 계층과 달리 입력 데이터(이미지)의 구조를 그대로 유지함. 가중치 역할을 하는 필터가 이미지를 슬라이딩하면서 공간적으로 내적을 수행함.

• 필터는 입력의 깊이(채널)만큼 확장되어 연산됨. (전체 깊이를 전부 취함)
  • 따라서 출력은 깊이가 1이 되며, 필터의 깊이는 입력 데이터의 깊이와 같아야 함.
• 행렬의 각 원소끼리 합성곱 연산을 하는 것은 사실 행렬을 쭉 펴서 D차원 벡터로 만든 후 내적을 하는 것과 같음.
  • 단, 필터가 적용되는 영역이 각 내적 간에 겹칠 수 있으므로, 쭉 편 후의 원소 수가 원본보다 더 많아질 수 있음.

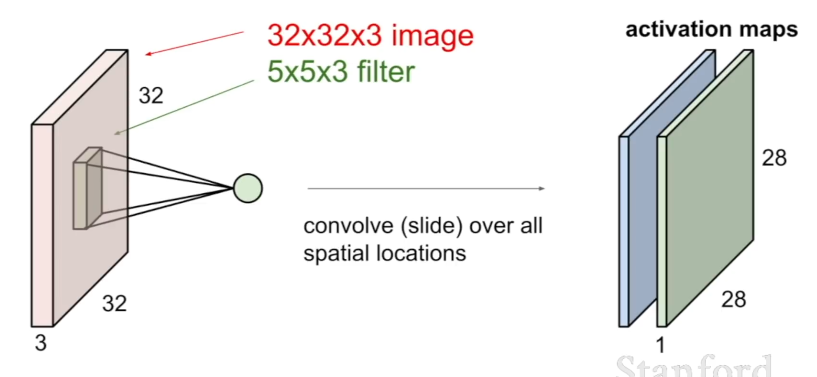
합성곱 계층에서는 여러 개의 필터를 사용하여 각 필터마다 다른 특징을 추출하도록 하며, 이때 필터 개수만큼의 서로 다른 Activation Map을 얻게 된다.

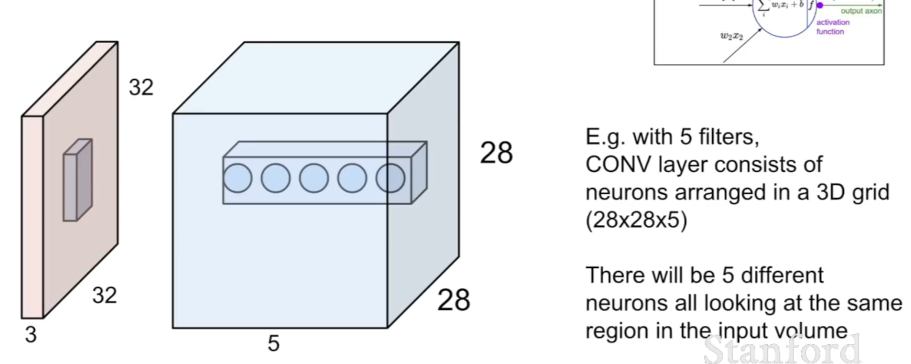
위 그림에서 파란색 육면체가 출력으로, 내부에 있는 5개의 점은 이미지의 동일한 위치에서 서로 다른 5개의 필터에 의해 추출된 서로 다른 특징들을 의미한다.

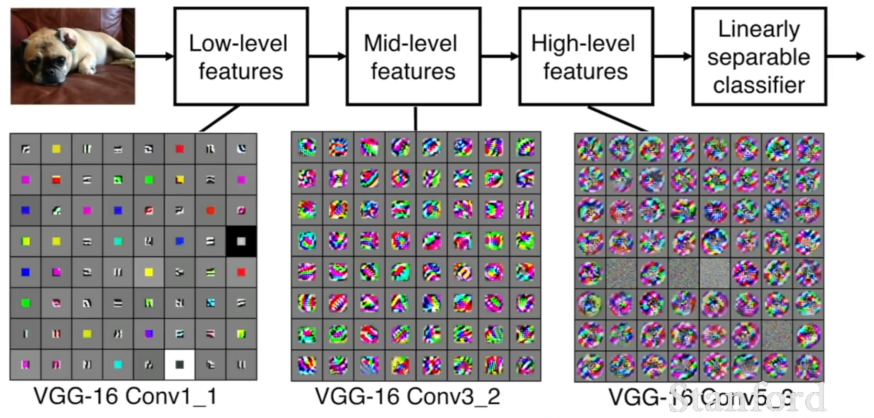
보통 CNN은 여러 겹의 합성곱 계층과 활성화 계층을 갖게 된다. 출력층에 가까운 필터일수록 점점 더 복잡한 형태의 특징을 학습하게 된다.

위 그림에서 각 그리드는 필터(뉴런)가 학습한 가중치를 시각화한 것으로, '입력 이미지가 어떻게 생겨야 해당 뉴런의 활성화 정도(출력)를 최대화 시키는지'를 나타낸다.

아무튼, 전체적인 CNN의 구조는 이런 식이다.

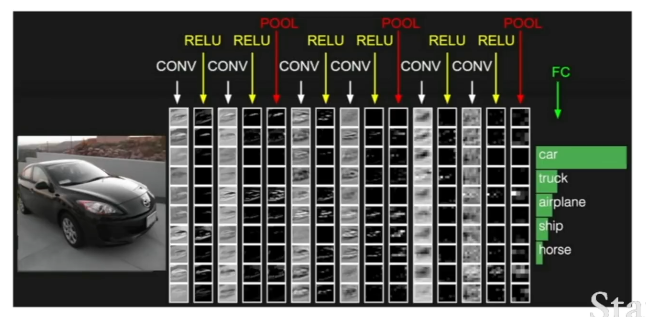
Spatial Dimensions

출력 행렬(Activation map)의 크기는 입력 행렬과 달라지게 되며, 입력 이미지와 필터의 크기, 슬라이딩 방법에 영향을 받는다.

• 수식: 출력 크기 = (입력 크기 - 필터 크기) / 스트라이드 + 1
• 스트라이드는 반드시 모든 이미지 영역을 커버할 수 있는 값으로 지정되어야 함.

한편, 입력 이미지에서 가장자리의 값은 필터의 중앙 부근에 닿지 않으므로 일종의 연산적인 불균형이 생길 수 있다. 이는 입력 이미지에 Zero-Padding을 추가하여 보완할 수 있다.

• 수식 (with 패딩): 출력 크기 = (입력 크기 + 2*패딩 - 필터 크기) / 스트라이드 + 1
• 패딩을 추가하는 것의 더 중요한 목적은 출력의 크기가 줄어들지 않도록 유지시켜 주는 데에 있다. 기본적으로 출력이 합성곱 계층을 거칠 때마다 작아지기 때문이다.

• 합성곱 계층에서의 총 파라미터 개수는 (각 필터를 구성하는 원소 수 + 편향 1개) * 총 필터 개수가 됨.
• 흔히 사용하는 하이퍼파라미터의 조합은 다음과 같음. (단, K=총 필터 수, F=필터 크기, S=스트라이드, P=패딩)
  

Pooling Layer

풀링 계층은 각 표현들을 더 작고 관리하기 쉽도록 Down-sampling(공간적으로 축소) 한다.

• 왜 작게 만드는가? ⇒ 작을수록 연산에 필요한 파라미터의 개수가 줄어듦.
• 반면, 깊이에는 아무 영향도 주지 않는다는 점에 유의할 것.

풀링 시에도 필터 크기를 정할 수 있으며, '얼마만큼의 영역을 묶을지'를 뜻한다. 스트라이드는 필터 적용 영역이 겹치지 않도록 주는 것이 일반적이다.

• 요즘은 풀링을 따로 수행하는 대신, 합성곱 계층에서 스트라이드를 주는 식으로 처리하는 것이 더 많다고 함.

Fully Connected Layer

CNN의 끝부분에는 완전 연결 계층이 존재하며, 마지막 합성곱 계층의 출력인 3차원 데이터를 전부 펴서 1차원 벡터로 만든 후 입력으로 사용한다.

공간적인 구조를 신경쓰지 않고 모든 출력을 전부 다 하나로 통합시켜 최종적인 추론을 하는 것이 역할이다. 예를 들어, 분류 문제의 경우 마지막에 각 카테고리에 대한 최종 점수를 산출하기 위해 소프트맥스가 활성화 함수로 사용된다.

6. Training Neural Network (1)

Activation Functions

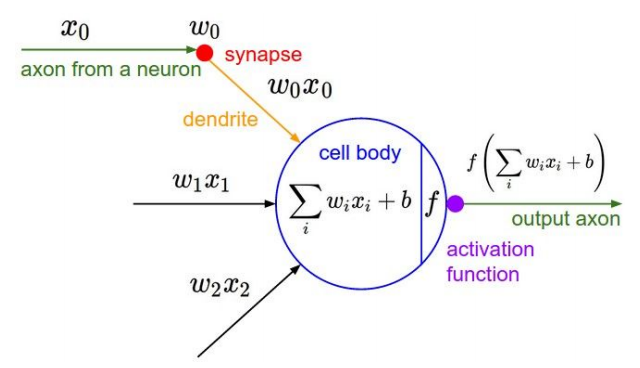
활성화 함수는 뉴런의 활성화 정도를 조정하고, 비선형의 힘을 가하는 역할을 한다.
대표적인 활성화 함수의 종류는 아래와 같다.

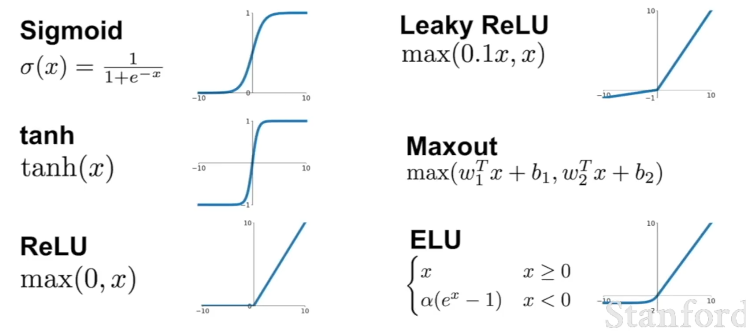
• Sigmoid: 입력을 받아서 [0, 1] 사이의 값이 되도록 함. (인간의 뉴런의 동작 방식과 비슷!)
  • 입력이 양 또는 음으로 큰 값이면 출력이 1 또는 0으로 수렴하면서 기울기가 0에 가까워지므로, 역전파 과정에서 이것이 연쇄되면서 기울기가 점차 소실되는 문제가 있음. (Saturation 현상 발생)
  • 또한, 출력이 'Zero-Centered'가 아니므로 그래디언트가 항상 '전부 양수' 또는 '전부 음수'가 되어 효율적인 갱신이 힘들 수도 있음.
    
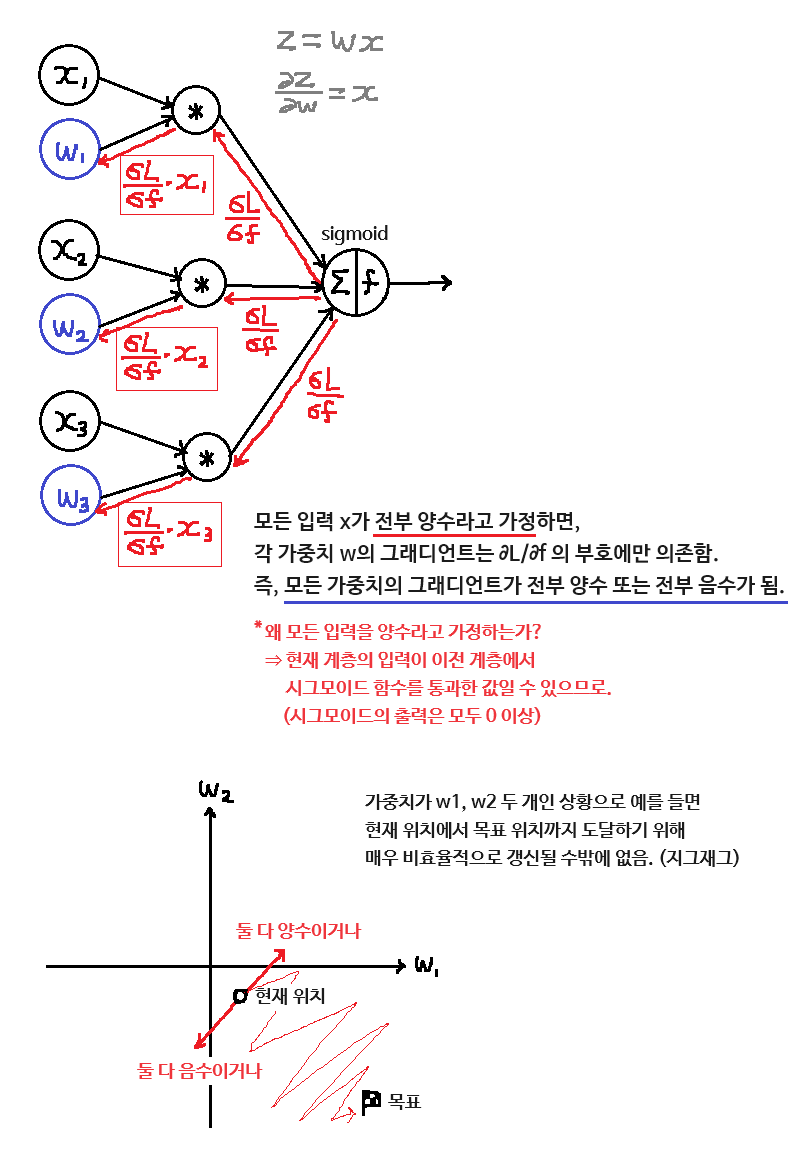
  • 추가적으로, $\exp(x)$ 항의 존재로 인해 계산 시간도 조금 오래 걸리는 편임.

• tanh(x): 시그모이드와 유사한 형태이나 범위가 [-1, 1]이므로 Zero-Centered 함.
  • 단, 여전히 양끝에서 기울기가 0에 가까워지므로 Saturation 현상이 발생함.

• ReLU(Rectified Linear Unit): 요소별(Element-Wise) 연산을 수행하며 입력이 음수면 0을, 양수면 그대로 출력함. (= $\max(0, x)$)
  • 양의 입력에서는 Saturation 되지 않으며 단순 최댓값 연산이므로 계산 효율도 매우 뛰어남. 생물학적 타당성도 시그모이드보다 더 뛰어남.
  • 그러나 Zero-Centered가 아니며 음의 입력에서는 여전히 Saturation이 발생함.
  • Dead ReLU: 어떤 입력에 대해서도 항상 0을 출력하며 가중치가 갱신되지 않는 '죽은 뉴런'. 가중치의 초기화를 잘못했거나 학습률이 지나치게 높은 경우 발생함.
    
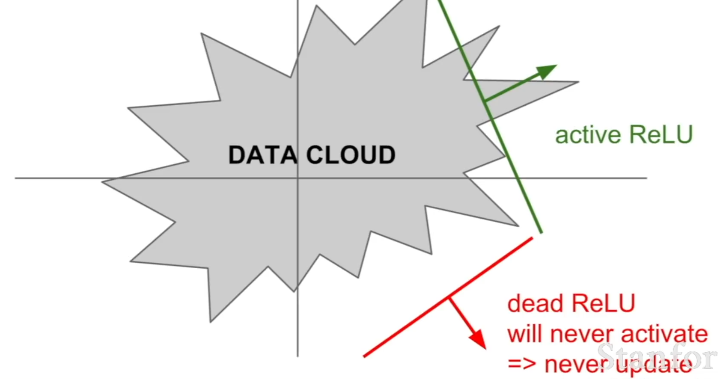
    • 발생 원인: 입력으로 들어온 가중치 합이 음수일 때 → ReLU의 출력은 0이고 기울기도 0이 됨 → 역전파 시 상류로부터 흘러온 그래디언트에 0을 곱하게 되므로 가중치를 갱신하지 못함!

• Leaky ReLU: 음의 입력에 대해서도 미세한 기울기를 추가하여 Saturation을 막음. (= $\max(0.01x, x)$)
• PReLU: Leaky ReLU와 유사하나, 미세 기울기를 임의의 고정된 값 대신 역전파를 통해 학습시키는 파라미터(α)를 통해 결정함. (= $\max(αx, x)$)
• ELU: ReLU와 Leaky ReLU의 중간 정도의 특성을 가짐. (Zero-Mean의 출력 + 음의 입력에서 Saturation)

• Maxout: $(w_{1})^{T}x + b_{1}$과 $(w_{2})^{T}x + b_{2}$중 큰 값을 취함. ReLU와 Leaky ReLU의 일반화된 형태.
  • 뉴런당 파라미터의 수가 두 배가 되어야 함.

📌 현재는 활성화 함수로 ReLU가 표준처럼 사용되며, Leaky ReLU와 Maxout, ELU도 실험적으로 사용되는 편이라고 한다. (시그모이드는 쓰지 말 것!)

Data Preprocessing

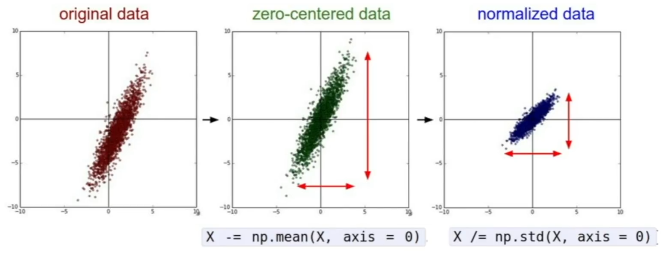
대표적인 전처리 과정은 'Zero-Mean'으로 만든 후 'Normalize'하는 것이다. 이 외에도 'Decorrelate', 'Whiten' 등의 전처리 방법이 있으나 이미지에서는 보통 'Zero-Mean'만 수행한다고 한다.

• Normalization: 모든 차원이 동일한 범위 안에 있도록 하여 '동등한 기여'를 하도록 함.
• Zero-Mean: 학습 데이터 전체를 대상으로, 3차원 형태의 '평균 이미지' 또는 채널별 평균값을 계산하여 빼주는 식으로 처리함.

Weight Initialization

학습을 시작하기 전, 가중치의 초깃값은 어떻게 정해야 할까? 모든 가중치를 0으로 두면 어떤 일이 벌어질까?

• 모든 가중치가 0이면 모든 뉴런이 동일한 연산을 수행하게 됨. 출력도 그래디언트도 같으므로 결국 모든 가중치가 똑같은 값으로 갱신됨.

그럼 임의의 작은 값으로 초기화 해보자. 예를 들어 표준정규분포에서 가중치를 뽑은 후 0.01배로 스케일링하여 사용해 보면 어떨까?

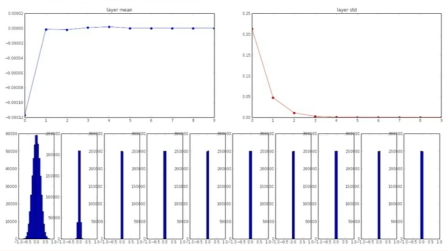
• 작은 네트워크에서는 문제가 안 되지만, 네트워크가 깊어지면 뒷쪽의 계층으로 이동할수록 가중치 $W$가 반복해서 곱해지므로 출력 값이 급격히 줄어듦. 즉, 모든 활성함수의 결과가 0이 됨.
• 역전파의 경우에도 그래디언트가 각 노드의 국소적 미분(Local Gradient)인 입력 $X$와 곱해지므로 점차 작아질 것이고 갱신이 잘 되지 않을 것임.

만약 가중치의 스케일링 값을 0.01이 아닌 1로 두면 어떻게 될까?

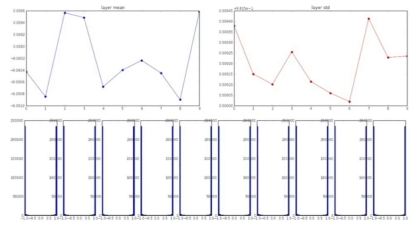
• 입력값이 크므로 tanh과 같은 활성화 함수에 의해 Saturation 되어 출력이 항상 -1 또는 +1이 될 것임. 그래디언트 또한 0이 되며 역시 갱신이 되지 않음.

따라서 가중치의 초깃값을 아무렇게나 두기 보다는, '널리 알려진 좋은 방법'을 사용하는 것이 좋다.

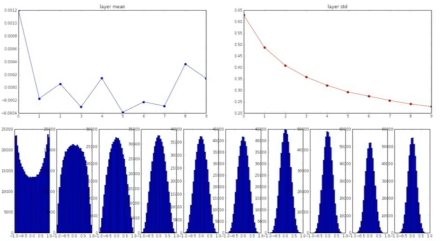
• Xavier Initialization: 정규분포에서 뽑은 값을 입력의 개수로 나누어 스케일링한 것을 사용함.
  • 입력의 수가 작으면 그만큼 작은 값으로 나눠지므로 더 큰 가중치를 얻고, 입력의 수가 크다면 반대로 더 작은 가중치를 얻게 됨. (⇒ 입력과 출력의 분산을 맞춰줌!)
  • 시그모이드 및 tanh 함수에서는 잘 동작하나, 출력의 절반을 매번 죽이는 ReLU에서는 분산을 반토막내므로 효과적이지 않음.
    • 입력의 개수 대신 (입력의 개수 / 2)를 나눠주는 식으로 보완할 수 있다!

Batch Normalization

우리는 각 계층의 출력이 'Unit Gaussian'을 따르길 원한다. 배치 정규화는 바로 그 역할을 한다.

배치 단위로 한 계층에 입력으로 들어오는 모든 값들을 이용해서 각 차원(Feature Element)별로 평균과 분산을 구하고, 이를 통해 정규화를 시켜준다.

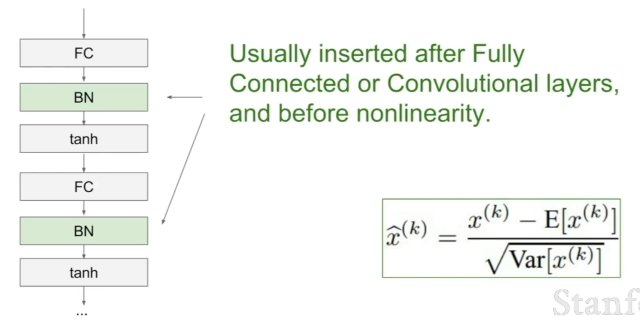
배치 정규화 계층은 완전 연결 계층 또는 합성곱 계층 바로 뒤에 붙여서 'Bad Scaling Effect'를 상쇄시켜 줄 수 있다.

이때 합성곱 계층에서는 각 차원마다 독립적으로 정규화하지 않고, 같은 Activation Map의 같은 채널에 있는 요소들을 다 같이 정규화한다. (즉, 각 깊이(채널)마다 평균과 분산을 하나씩)

정규화 이후에는 스케일링 및 쉬프트 연산을 통해 정규화 정도(= Saturation 되지 않는 정도)를 조정한다. 중요한 점은 스케일링 인자 $\gamma^{(k)}$와 쉬프트 인자 $\beta^{(k)}$는 네트워크가 학습 가능한 파라미터라는 것이다.

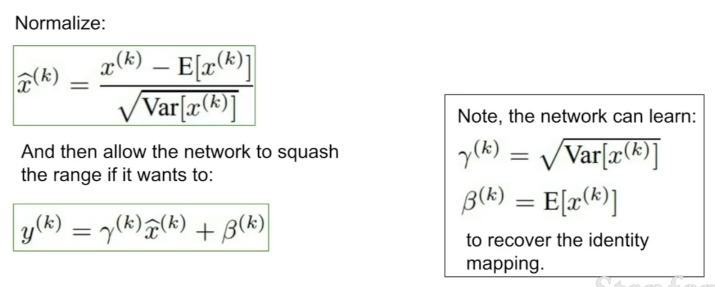
배치 정규화를 거치면 그래디언트의 흐름을 원활하게 하여 빠르고 효과적인 학습을 가능하며, 각 계층의 출력이 하나의 데이터에 결정적인 값이 아닌 배치 내의 전체 데이터와 연관되는 효과를 준다. (= Regularization)

• 학습을 마친 뒤 시험 단계에서는 추가적인 계산 없이 학습 과정에서 구해놓은 평균 및 분산을 사용한다.
• 결과적으로, 필요한 수식들을 정리하면 다음과 같다.
  

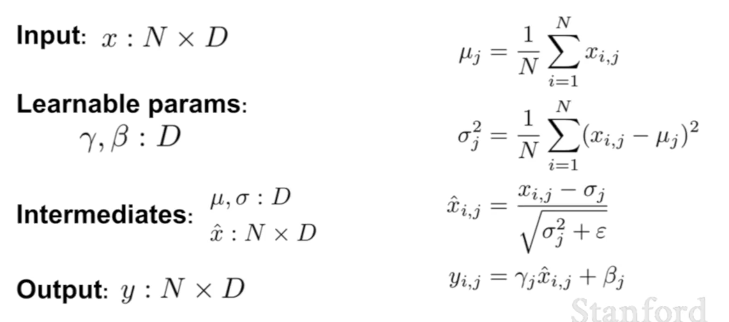
학습 과정 분석 및 관리

전체적인 신경망의 학습 과정은 다음과 같다.

1. 데이터 전처리
2. 아키텍처 선택 (ex. 각 레이어의 뉴런 수)
3. 네트워크 초기화 및 초기 손실 값의 정상 여부 확인
4. 본 학습 전, 적은 데이터를 통해 오버피팅을 발생시켜 손실 값의 감소 여부 확인
5. 학습률을 조절하면서 적절한 값을 찾아 선택 (보통 1e-3~1e-5 사이의 값을 사용)
6. 그 외 하이퍼파라미터 선택

📌 간혹 손실(Loss)과 정확도(Accuracy)가 비례하여 감소하지 않는 경우가 있는데, 이는 뭔가가 잘못됐다기보단 두 값의 정의가 다르기 때문이다.

1. Loss: 모델이 예측한 결과와 정답 사이의 '거리'
2. Accuracy: 전체 예측 결과 중 정답인 것의 '비율'

• Cross-Validation 전략: 하이퍼파라미터 후보의 범위를 먼저 정해놓고, 학습을 진행하면서 정확도가 높게 나온 것을 기준으로 다시 범위를 좁혀나가는 것을 반복함.
  • 처음엔 로그 스케일로 크게 값을 주는 것이 좋음. (학습률은 그래디언트와 곱해지기 때문에)

• Grid Search: 하이퍼파라미터 후보를 고정된 값과 간격으로 샘플링하는 것. 하지만 실제로는 그냥 랜덤으로 뽑는 것이 더 좋음. (중요한 파라미터에서 더 다양한 샘플링 가능!)
  

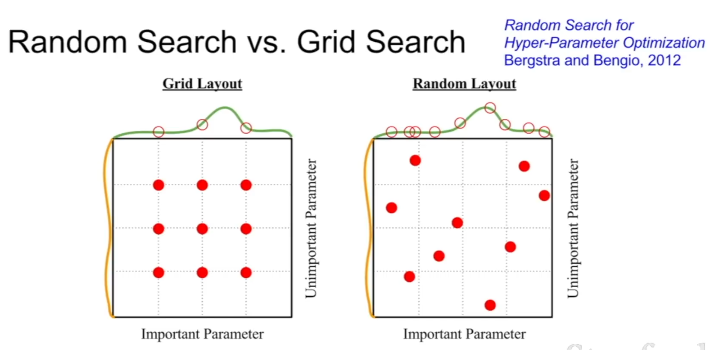
하이퍼파라미터를 선택하는 일은 실제로 꽤 어렵고 예술의 영역에 가깝다고 한다...
학습 상태를 잘 모니터링하면서 적절한 하이퍼파라미터를 결정할 수 있도록 하자.

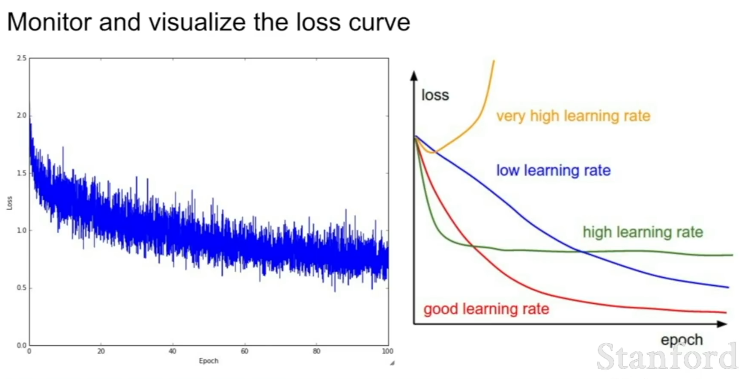
• 손실이 초기에는 평평하다가 갑자기 가파르게 내려간다면(= Loss Curve) 주로 초기화의 문제일 가능성이 크며, 이는 처음에 역전파가 잘 이뤄지지 않다가 학습이 진행되면서 회복되는 것임.
• 훈련 정확도와 검증 정확도의 차이가 너무 크다면 오버피팅의 확률이 높으므로 Regularization의 강도를 높여야 함.
• 가중치의 크기 대비 가중치의 갱신 크기 비율은 0.001 정도가 되는 것이 좋음. (Norm을 이용하여 데이터의 규모 측정 가능)

7. Training Neural Network (2)

Problems of SGD

기존 SGD 방식의 문제 중 하나는 손실 함수가 '한 방향의 가중치 변화에는 매우 민감하지만, 다른 방향으로는 둔감한' 형태를 갖고 있다면 (또는 현재 지점에서의 기울기의 방향과 실제 최솟값이 위치한 방향이 다르다면) 그래디언트가 매우 비효율적으로 갱신된다는 것이다.

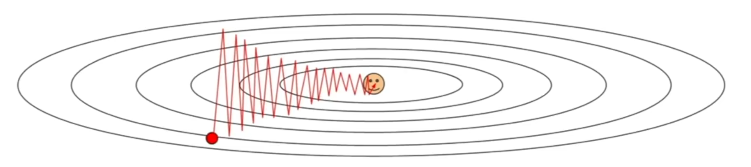
• 실제 신경망에는 가중치가 이보다 훨씬 많으므로, 불균형한 방향이 존재할 확률이 높아지니 더더욱 문제가 될 것이다.

또한, 손실 함수에 Local Minima(극소점)이나 Saddle Point(안장점)이 존재할 경우, 최솟값이 아님에도 기울기가 0이므로 그곳에서 갱신이 멈춰버릴 수도 있다.

• 안장점은 어떤 방향으로는 값이 증가하고 어떤 방향으로는 값이 감소하는 지점이다. 즉, 가중치의 수가 많은 고차원 공간일수록 모든 방향으로 손실이 증가하는 극소점에 비해 훨씬 빈번하게 나타난다.

또한, SGD는 전체 데이터 대신 미니배치의 데이터를 통해 손실을 계산하므로(= 'Stochastic') 실제 그래디언트가 아닌 Noisy Estimate(추정값)만을 구하게 되고 이 역시 갱신을 비효율적으로 만든다.

SGD + Momenturm

이런 문제를 해결하기 위해 SGD에 '모멘텀'을 추가할 수 있다.

방법은 매우 간단하다. 기존 SGD에서 기울기를 갱신하는 수식의 끝에 Velocity(속도)의 역할을 하는 항을 추가하면 된다.

• rho는 Velocity의 영향력을 조정하는 하이퍼파라미터로, 대략 0.9 또는 0.99 정도로 설정한다.

이렇게 되면 손실 함수에서 매 지점의 기울기에만 의존하는 대신, 일종의 속도를 지니게 되므로 기울기가 0인 지점을 만나더라도 탈출할 수 있는 힘을 갖게 된다.

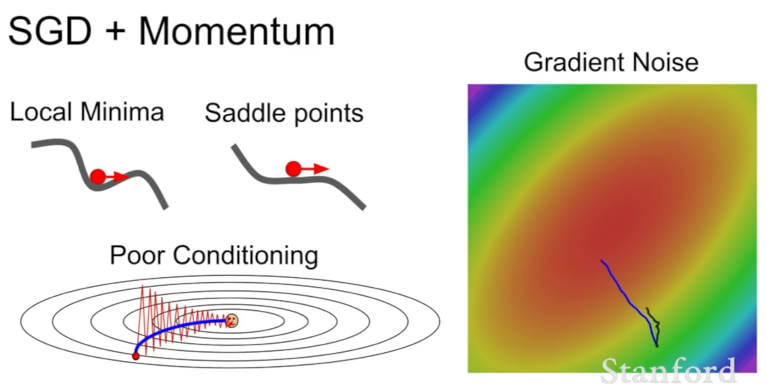
• 속도는 방향이 자주 변동되는 축으로는 감속, 방향이 유지되는 축으로는 가속되는 효과를 부여한다. '노이즈를 평균화한다'라고도 할 수 있다.

Nesterov Momentum

먼저 Velocity의 방향으로 한 번 이동한 후, 해당 지점에서의 그래디언트 방향으로 다시 한 번 이동하는 방법이다.

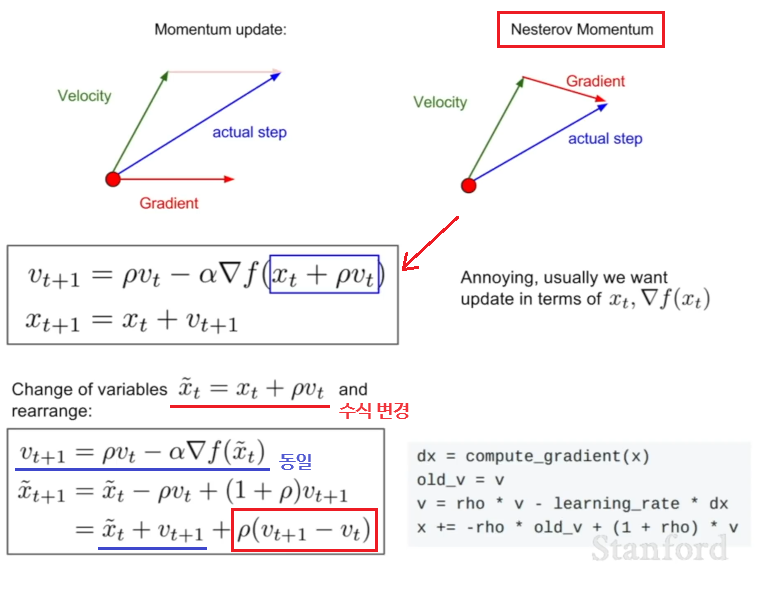
• Velocity의 방향이 잘못되었을 경우에 현재의 그래디언트의 방향을 좀 더 활용할 수 있게 해줌.
• Convex Optimization 문제에서 뛰어난 성능을 보인다고 함.

💡 'Convex'란?

'볼록 함수'에서의 볼록하다는 뜻으로, 여기서는 기울기가 0이 되는 지점이 곧 Global Minimum인 환경을 뜻한다. 즉, 경사하강법을 통해 반드시 최솟값을 찾을 수 있음이 보장된다.

반대로 'Non-convex' 하다는 것은 극솟값, 안장점 등 여러 Local Minimum이 존재하는 환경을 말한다.

AdaGrad

학습 과정에서 계산되는 매 그래디언트의 제곱을 누적한 값(Grad Squared Term)으로 현재 단계에서 갱신될 값을 나눠주는 방법이다.

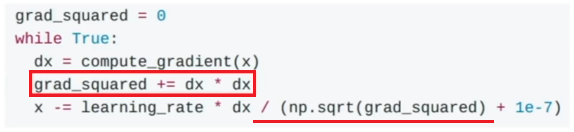
• 각 차원마다 그래디언트의 제곱 항으로 '나누게' 되므로 그래디언트가 작으면 가속하고, 크면 감속하는 효과가 있음.
• 학습 횟수가 늘어날수록 제곱 항이 점점 누적되므로, 이것으로 나눠지는 Step Size가 점점 작아지는 문제가 있음.
  • 손실 함수가 convex 한 경우, 최솟값에 다가갈수록 점차 느려지면서 수렴하므로 좋은 특징이 되지만, non-convex 한 경우라면 극솟값, 안장점 등에서 멈춰버릴 수 있으므로 좋지 않음.

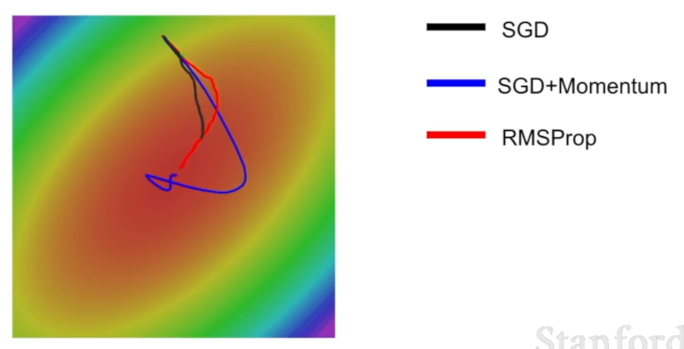
RMSProp

AdaGrad의 문제를 개선한 방법. 제곱 항을 누적할 때 Decay Rate를 곱해서 더해준다. (모멘텀과 비슷!)

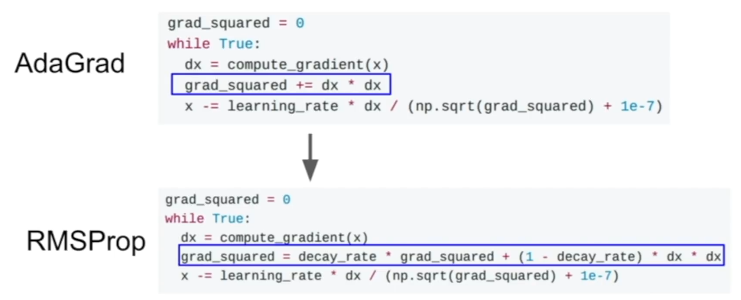
• 정확히는 누적 제곱 값에 Decay Rate를 곱하고, 현재 그래디언트의 제곱에 '(1 - Decay Rate)'를 곱한 값을 서로 더해서 사용함.
• Decay Rate는 0.9 또는 0.99를 주로 사용함.
• Momentum은 목표 지점보다 더 이동한 뒤 다시 최솟값을 향해 돌아오는 형태지만, RMSProp은 각 차원마다의 상황에 맞도록 적절하게 궤적을 수정함.
  

Adam

Momentum과 RMSProp을 절반씩 조합한 방법으로, 거의 모든 아키텍쳐와 다양한 문제에서 매우 잘 동작하는 방법이다. 기본 코드는 다음과 같다.

위 코드의 문제는 처음엔 second_moment 값이 매우 작으므로 초기 Step이 매우 커진다는 것이다. Adam에서는 이를 보완하기 위해 Bias Correction 항을 추가한다.

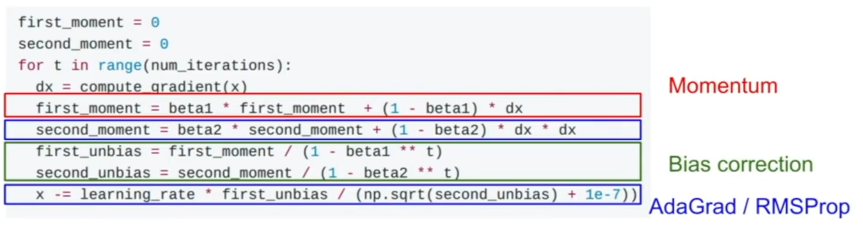
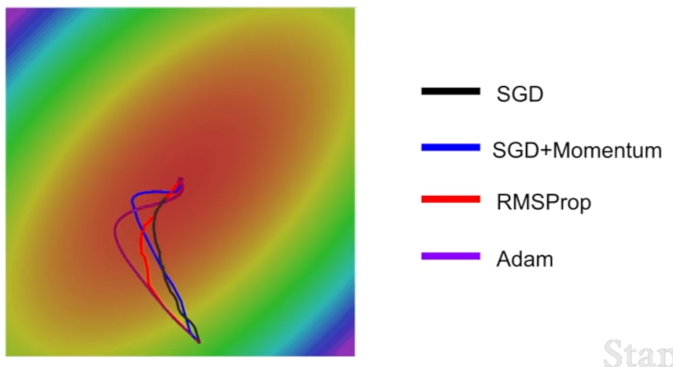
• beta_1은 0.9, beta_2는 0.999, 학습률은 1e-3~1e-4 정도를 사용한다.
• 실제 동작하는 모습을 보면 Momentum처럼 살짝 오버슈팅하면서도 RMSProp처럼 각 차원마다의 상황을 고려하여 움직이는 것을 볼 수 있다.
  

Learning Rate Decay

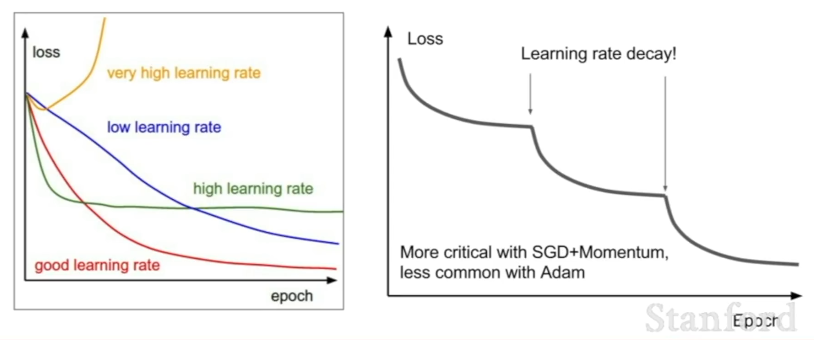
Loss가 일정 값으로 수렴한다는 것은 학습률이 너무 높아서 더 좁은 곳으로 들어가지 못하고 계속 왔다 갔다(Bouncing Around) 하고 있다는 뜻일 수 있다. 이때 임의로 학습률을 낮추는 기법이 사용된다.

• Adam보다는 SGD Momentum을 사용할 때 자주 사용됨.
• 물론 임의로 학습률을 낮추는 것은 부차적인 방법이므로, 초기에 학습률을 잘 선택하는 것이 더 중요함.

Second-Order Optimization

지금까지의 방법은 1차(First-Order) 미분만을 사용한 방법이었다.

어느 한 점에서의 1차 미분을 통해 그래디언트를 얻고, 그로부터 손실 함수를 선형 함수로 근사한 뒤, 근사 함수를 실제 손실 함수라고 가정하고 내려가는 것이다.

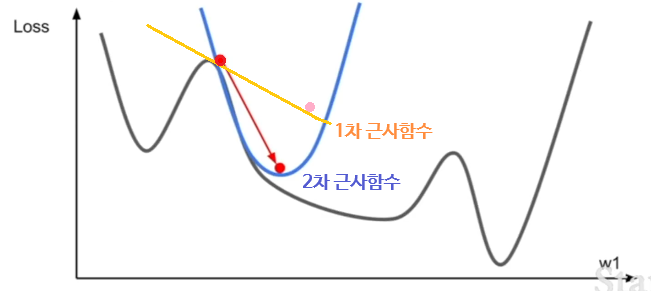
반면, 2차(Second-Order) 근사를 이용하면 근사 함수가 선형 함수가 아닌 2차 함수의 모양이 되며, 최솟값에 더 잘 근접할 수 있다. 이 개념을 다차원으로 확장시킨 것을 'Newton Step'이라 한다.

• Hessian Matrix: 다변수 함수에 대한 2차 미분값들로 이루어진 행렬. 이것의 역행렬을 이용해 손실 함수의 2차 근사를 구할 수 있음.
  • 헷갈리기 쉬운 Gradient, Jacobian Matrix, Hessian Matrix에 대해서는 이 게시글을 참고하자.

Newton Step의 가장 큰 특징은 Learning Rate가 불필요하다는 것이다. 하지만 실제로는 Hessian Matrix의 크기가 N×N으로 매우 크기 때문에 바로 딥러닝에 사용할 수는 없다.

• L-BFGS: Hessian을 근사시켜서 사용하는 Second-Order Optimization 기법. Full Batch Update가 가능하고 Stochasticity 및 파라미터가 적은 경우 사용될 수 있음.

Model Ensembles

지금까지의 방법들은 훈련 단계에서 손실 함수를 최소화하기 위한 방법이었다. 하지만 정말 중요한 건 훈련 오차와 검증/시험 오차 간의 격차를 줄이는 것이다.

즉, 손실 함수에 대한 최적화를 마친 상황에서 '한 번도 보지 못한 데이터'에 대한 성능을 올려야 한다. 모델 앙상블은 그 방법 중 하나이다.

모델 앙상블에서는 여러 개의 모델을 독립적으로 학습시킨 후 각 모델별 결과의 평균을 이용한다. 약 2%의 성능 향상을 기대할 수 있다고 한다.

• 각 모델을 독립으로 학습시키는 대신, 학습 도중 중간 모델들을 저장한 것(스냅샷)을 앙상블로 사용할 수도 있음. 시험 단계에서 각 스냅샷에서 나온 예측값들을 평균 내어 사용함.
• 학습률을 크게 낮추었다가 다시 크게 올리는 것을 반복하면서 손실 함수의 다양한 지역에 수렴할 수 있도록 만드는 기법도 있음.

Dropout

드롭아웃은 신경망에서 주로 사용하는 Regularization 기법으로, 각 순전파 과정마다 임의의 일부 뉴런을 0으로 만든다.

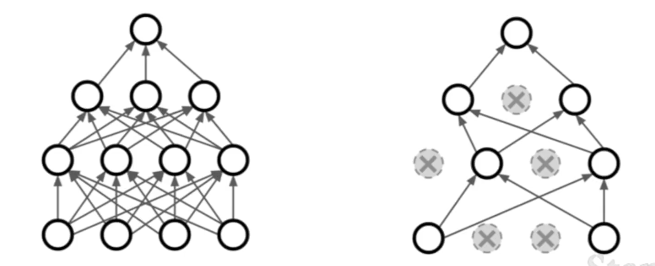
• 드롭아웃은 한 계층씩 진행함. 한 계층의 출력을 전부 구하고, 임의의 뉴런을 0으로 만들고, 다음 계층으로 넘어가는 식.
• 0이 되는 뉴런은 각 순전파마다 바뀌므로, '원래 네트워크의 작은 버전'(= 서브네트워크)이 매번 새롭게 만들어지는 것과 같음.

코드도 매우 간단하다. 각 계층마다 일정 확률(주로 0.5)로 뉴런을 통과시키는 랜덤한 마스크를 생성하여 적용하면 된다.

드롭아웃은 특징들 사이의 상호작용(Co-Adptation)을 방지한다. 네트워크가 일부 특징에만 과도하게 의존하는 것을 막고 모든 특징을 골고루 이용할 수 있게 한다.

또한 드롭아웃을 이용하면 단일 모델만으로 앙상블 효과를 얻을 수 있다. 파라미터를 공유하는 거대한 서브네트워크 앙상블을 동시에 학습시키는 것과 비슷하기 때문이다.

드롭아웃은 기존 신경망에 랜덤한 마스크(z)라는 '임의성(Stochasticity)'을 부여한다. 하지만 시험 단계에서 임의성을 추가하는 것은 좋지 않으므로, 일종의 'Average-Out(평균을 내어 상쇄)' 하는 절차가 필요하다. 이때 필요한 복잡한 적분식을 직접 푸는 대신 간단히 근사화하여 해결하는 방법이 있다.

훈련 단계와 시험 단계에서 각 네트워크의 출력의 기댓값을 비교해 보면, '뉴런이 임의로 0이 될 확률'(= Dropout Probability)에 따라 차이가 발생하는 것을 볼 수 있다. 이 두 기댓값의 차이를 메우는 방법은 시험 단계에서 각 네트워크의 출력에 드롭아웃 확률만큼의 값을 곱해주는 것이다.

• 시험 단계에서의 연산량을 최대한 줄이기 위해, 역으로 훈련 단계에서 P를 나눠주는 방법도 가능함!
• Batch Normalization을 사용할 때는 이미 충분한 Regularization 효과를 얻을 수 있으므로 Dropout을 사용하지 않음.

📌 Regularization 기법의 공통적인 특징은 훈련 단계에서 임의성을 추가하여 신경망이 훈련 데이터에 과하게 적응하지 않도록 방해하고, 시험 단계에서 추가했던 임의성을 평균화 시키는 것이다.

Data Augmentation

훈련 단계에서 데이터(이미지)의 레이블을 바꾸지 않으면서 무작위로 변환(좌우반전, 크롭 등)하여 학습 시키는 기법으로, 일종의 Regularization 효과를 얻을 수 있다.

시험 단계에서는 임의성을 평균화하기 위해 이미지를 '4개의 가장자리'와 '중앙' 부위로 잘라내고, 또 이것의 반전 버전을 만들어서 총 10개의 이미지를 사용한다.

Other Regularizations

그 외에 강의에서 소개된 Regularization 기법들에는 이런 것들이 있다.

• DropConnect: Activation이 아닌 Weight Matrix를 임시적으로 0으로 만들어주는 방법.

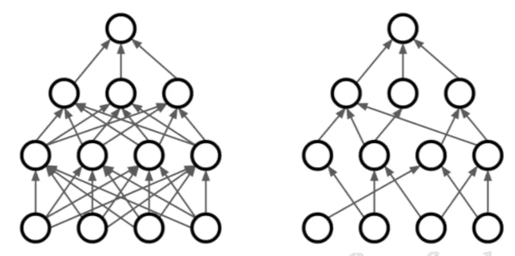
• Fractional Max Pooling: 훈련 단계에서 풀링을 고정된 영역이 아닌 임의의 영역에서 수행하고, 시험 단계에서 다시 풀링 영역을 고정시키거나 여러 개의 영역을 만들어 평균을 내는 식으로 처리함.

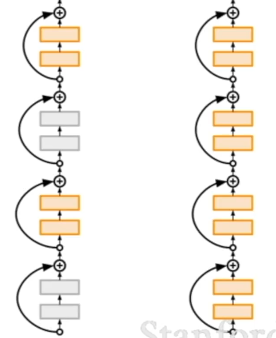
• Stochastic Depth: 훈련단계에서 일부 계층을 제거하고 일부만 사용해서 학습한 후, 시험 단계에서 전체 네트워크를 사용함.

Transfer Learning

ImageNet과 같은 매우 큰 데이터셋으로 학습된 기존 CNN으로부터, 학습된 특징들을 이용해 더 작은 데이터셋을 가진 다른 유사한 문제를 푸는 모델을 만들 수 있다. 이러한 방법을 전이 학습이라 부른다.

1. 기존에 학습을 마친 CNN에서 가장 마지막의 완전 연결 계층(= 최종 특징과 클래스별 점수 간 연결)을 초기화함. (이때, 새로운 문제에 맞게 차원을 바꿔줌)
2. 나머지 이전 모든 계층들의 가중치는 Freeze 시킴.
3. 이는 곧 선형 분류자를 학습시키는 것과 같음. (오직 마지막 계층만으로 새로운 데이터를 학습!)

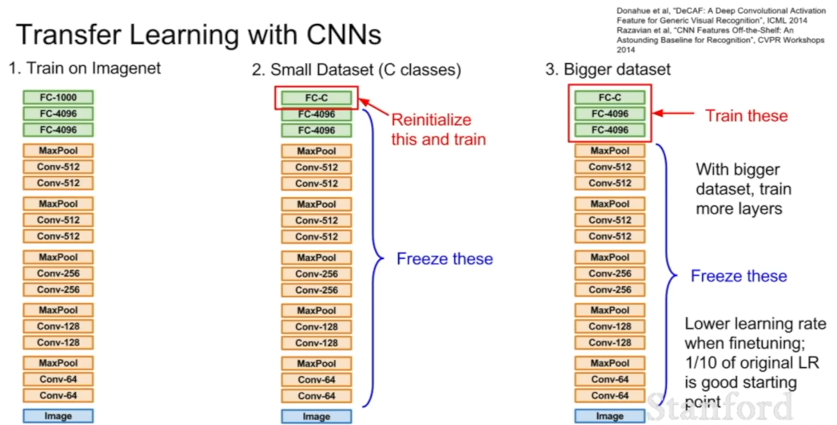
만약 데이터가 좀 더 많다면 전체 네트워크를 'Fine-Tuning' 할 수도 있다. 즉, 한 계층이 아닌 좀 더 많은 부분을 갱신할 수 있는 것이다.

• 단, 전이 학습 시에는 학습률을 조금 낮춰서 진행하는 것이 좋음. (이미 한 번 학습을 마친 모델을 재사용하는 것이므로)
• CNN의 전이 학습은 매우 흔하며 자주 이용되는 기법임. 오히려 밑바닥부터 학습시키는 경우가 더 드묾!

---

정리

'밑바닥부터 시작하는 딥러닝'을 먼저 읽은 후 이번 강의를 들어 보았는데, 책에 비해 어떤 부분은 더 간단히만 짚은 후 넘어가기도 했고, 또 어떤 부분은 더 깊고 자세한 내용까지 다루기도 한 느낌이다. 일단은 강의 전반부(1~7강)에서 해당 책이 담고 있던 범위의 대부분을 다룬 것 같다.

강의 후반부에서는 아마 조금 더 CNN, 컴퓨터 비전과 관련된 내용이 나올 것 같다. 지금까지 배운 내용 중 부족한 부분을 복습한 후 넘어가야겠다.