CS231n 강의 정리 (8~14강)

스탠포드 대학교의 CS231n 강의를 듣고 요약, 필기한 글입니다.

8. Deep Learning Software

CPU vs GPU

• CPU: 적은 수의 빠르고 똑똑한 코어들이 독립적으로 작업을 처리함, 멀티 스레딩 가능, 작은 캐시 메모리를 가짐, 범용적인 작업에 적합함.
• GPU: 수천 개의 느리고 단순한 코어들이 하나의 작업을 병렬적으로 처리함, 칩 안에 자신만의 메모리(VRAM)를 내장함.

대표적으로, 행렬곱 연산은 GPU가 처리하기에 아주 적합한 연산이다. 결과 행렬의 각 원소들이 독립적인 계산(두 벡터의 내적)을 통해 구해지므로 모두 병렬로 처리할 수 있기 때문이다.

CPU/GPU Communication

GPU로 학습을 진행할 때 모델과 가중치는 전부 GPU 메모리에 올라가 있는 반면, 실제 훈련 데이터는 SSD와 같은 드라이브 내에 존재하므로 I/O 수행 시 병목이 생길 수 있다.

• 방안 1. 데이터셋이 작거나 메모리 용량이 크다면 전체 데이터셋을 메모리에 올려놓기
• 방안 2. CPU의 다중 스레드를 이용하여 데이터를 메모리에 미리미리 불러오기 (= Pre-Fetching)
  • 프레임워크를 사용하면 이러한 작업들을 알아서 처리해 준다!

Deep Learning Framework

프레임워크를 사용하면 실제 DNN의 복잡한 계산 그래프를 직접 그리지 않아도 되며, 순전파 코드만 잘 작성하면 역전파 및 그래디언트를 자동으로 계산할 수 있고, GPU까지 쉽고 효율적으로 이용할 수 있다.

강의에서는 여러 딥러닝 프레임워크 중 가장 유명한 PyTorch와 TensorFlow를 소개한다. 아래는 두 프레임워크를 사용하여 간단한 신경망 학습 코드를 작성한 예시이다.

파이토치와 텐서플로 모두 넘파이와 비슷한 형태로 코드를 작성할 수 있으며, 손쉽게 그래디언트를 얻거나 GPU 사용 여부를 지정해 줄 수 있다.

📌 현재 시점(2024년)에는 강의(2017년)에서 소개된 몇몇 프레임워크 관련 설명이 맞지 않는다. 따라서 정확한 문법이나 사용 예시보다는 큰 그림 위주로만 정리하였다.

Static Graph vs Dynamic Graph

텐서플로가 그래프를 명시적으로 구성한 후(Static Graph) 계산을 시작했다면, 파이토치는 순전파를 수행할 때마다 매번 그래프를 다시 계산(Dynamic Graph)한다는 큰 차이점이 있다.

• Static Graph: 한 번 구성한 계산 그래프를 학습 과정에서 매우 많이 재사용하게 되므로, 학습 시작 전 최적화 작업을 수행하면 얻는 이점이 많아짐.
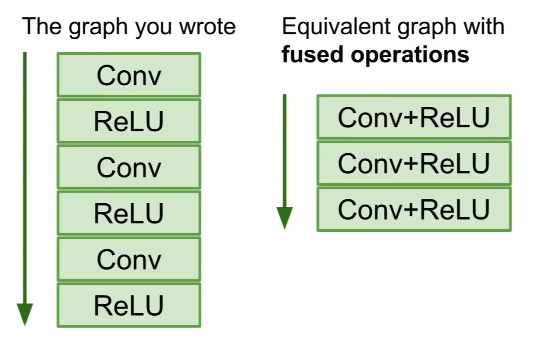  또한, 그래프를 한 번 구성해 놓으면 메모리 내에 해당 네트워크 구조가 들어있다는 뜻이므로, 손쉽게 Serialization(직렬화)하여 파일 형태로 저장하거나 불러올 수 있음.

• Dynamic Graph: 대다수의 경우에 코드가 훨씬 더 깔끔하고 쉬움. 예를 들어 조건 분기문이 있을 때에도 매번 새롭게 그래프를 생성하므로 하나의 선택지만 택하여 그래프를 만들어도 상관없음. 즉, 일반적인 if 문을 사용해서 코드 작성이 가능함.
  또한, 반복/재귀적인 연산의 경우에도 연산 대상의 크기를 매번 고려하지 않아도 되므로 역시 일반 파이썬의 반목문만으로도 처리가 가능함.
  
  • 반면, 텐서플로에서는 계산 그래프의 전체 흐름을 미리 다 구성해 두어야 하므로 추가적인 문법이 필요하며 코드가 지저분해짐.
  • Dynamic Graph는 이미지 캡셔닝(Recurrent Network), 자연어 처리(Recursive Network) 등 다양한 분야에 이용될 수 있음.

📌 강의에서는 범용적인 목적으로는 텐서플로를, 연구 목적이거나 Dynamic Graph가 필요한 상황에서는 파이토치를 추천한다. (현재 시점에서는 파이토치의 위상이 더욱 높아진 것 같다) 두 프레임워크에 대한 더 자세한 비교는 이 게시글을 참고하면 좋을 것 같다.

9. CNN Architectures

LeNet-5 (1998)

산업에 성공적으로 적용된 최초의 CNN으로, 매우 간단한 모델임에도 숫자 인식에서 엄청난 성공을 거두었다.

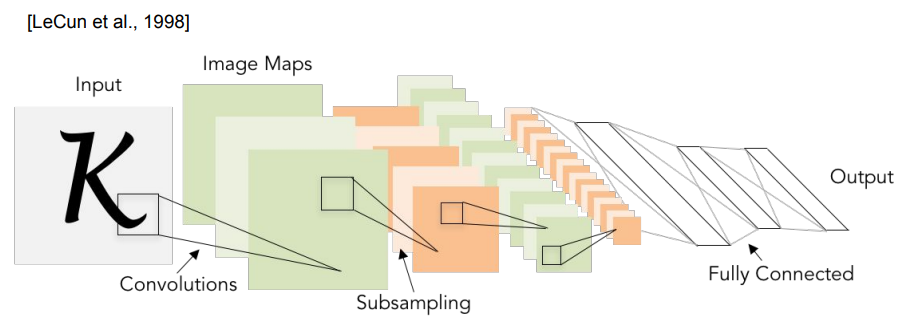
LeNet은 이미지를 입력으로 받아 스트라이드=1, 5×5 크기의 필터를 갖는 합성곱 계층과 풀링 계층을 거친 후, 마지막으로 완전 연결 계층을 거쳐 10개의 분류 점수를 출력한다.

AlexNet (2012)

최초의 Large Scale CNN으로, ImageNet 분류에서 매우 뛰어난 성능을 보여준 네트워크이다.

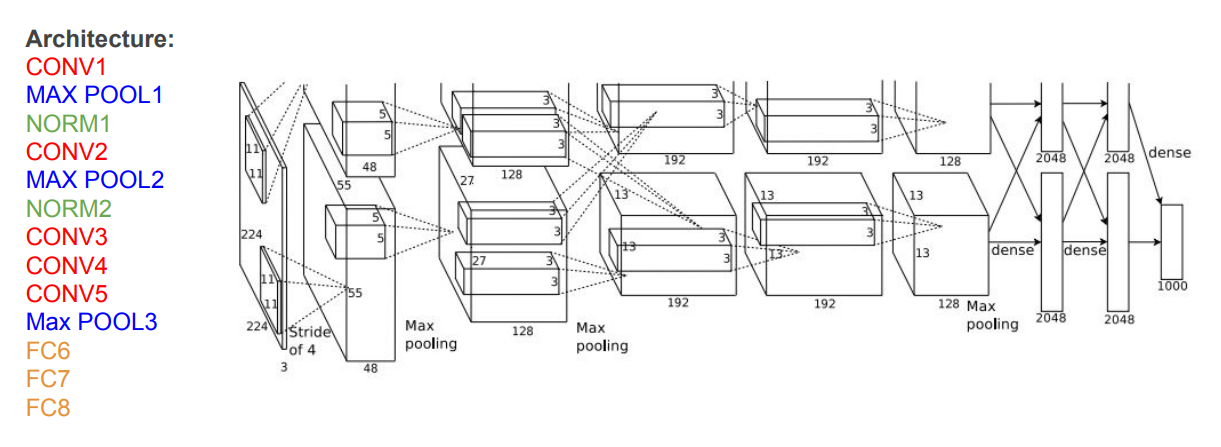
• 입력은 227×227×3 크기의 이미지이며, 5개의 합성곱 계층과 3개의 완전 연결 계층으로 구성됨.
• 마지막 완전 연결 계층에서는 소프트맥스 함수가, 나머지 계층에서는 ReLU가 활성화 함수로 사용됨.

각 계층의 자세한 구조와 출력 크기는 다음 이미지를 참고하자.

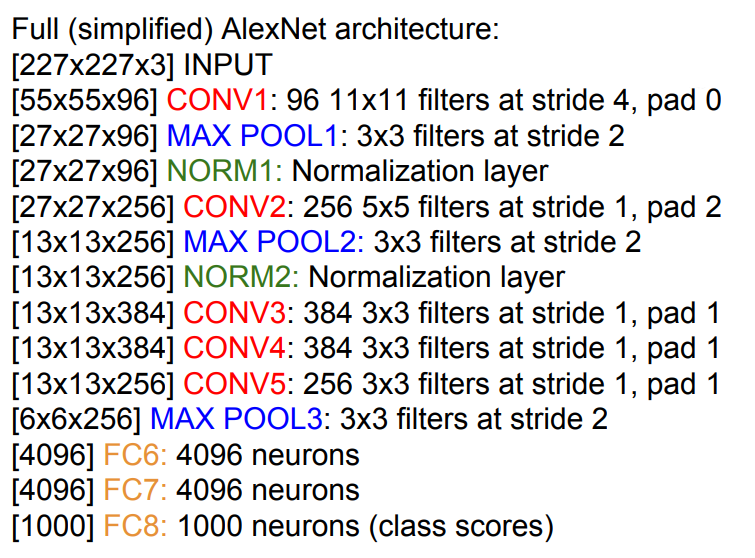
📌 파라미터란 우리가 학습시키는 가중치를 말한다. 즉, 합성곱 계층에선 필터가 곧 파라미터이며, 풀링 계층에선 파라미터가 없다.

AlexNet에 대한 기타 세부적인 특징은 이렇다.

• 많은 Data Augmentation를 수행함.
• Weight Decay, 모델 앙상블, 드롭아웃 기법을 사용함.
• 학습 시 배치 크기는 128임.
• SGD Momentum을 사용함.
• 초기 학습률은 1e-2이며, 정확도가 올라가지 않는 지점에서 학습이 종료될 때까지 1e-10까지 줄임.

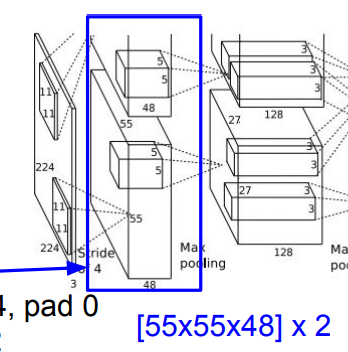
AlexNet의 첫 번째 합성곱 계층을 보면 모델이 두 개로 나눠져서 연산되는 것을 볼 수 있다. (출력의 깊이 또한 96이 아닌 48로 표시됨!) 이는 당시 GPU 메모리의 한계로 인해 네트워크(뉴런 + 특징 맵)를 2개로 분산하여 2개의 GPU가 각각 맡도록 했기 때문이다.

따라서 1,2,4,5번째 합성곱 계층은 전체 96개의 특징 맵을 볼 수 없으며 자신이 맡은 48개의 특징 맵만을 사용한다. 하지만 3번째 합성곱 계층과 완전 연결 계층들은 이전 계층의 '전체 특징 맵'과 연결되어 있으므로 (즉, GPU 간의 통신이 이루어지므로) 전체 깊이를 전부 가져올 수 있다.

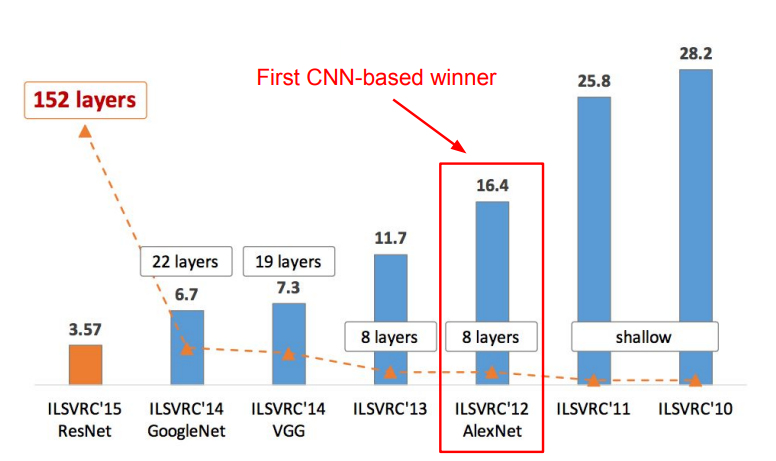
AlexNet은 ILSVRC에서의 최초의 CNN 기반 우승 모델이며, 꽤 오랜 기간 동안 CNN 아키텍처의 베이스 모델로 사용되었다.

• ZFNet (2013): AlexNet의 하이퍼파라미터를 개선한 모델. 기본 구조나 아이디어는 같음.
• AlexNet의 구조에 대한 더 자세한 분석은 이 게시글을 참고하자.

VGGNet

AlexNet보다 훨씬 더 깊은 네트워크 구조(16 or 19개의 계층)를 가지며, 더 작은 필터(3×3 크기)를 사용한다. 아주 간단하면서도 고급진 아키텍처.

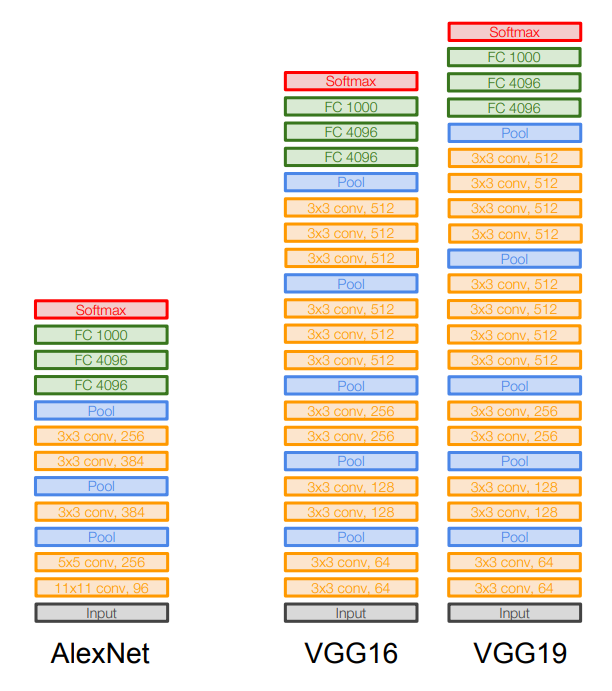
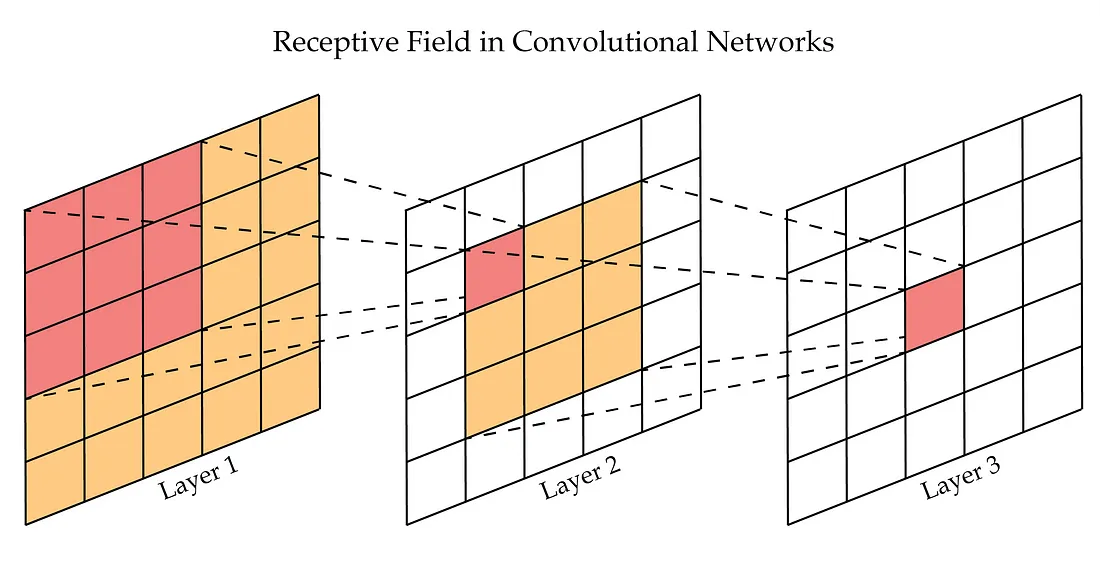
VGG가 작은 필터를 사용하는 이유는 필터의 크기가 작을수록 파라미터 수를 줄이면서도 계층을 더 깊게 만들 수 있기 때문이다. 가령, 3×3 필터를 3개의 계층으로 구성한 것은 7×7 필터를 한 번만 거치는 것과 실질적으로 동일한 Receptive Field를 가지지만, 전체 파라미터 수는 줄어들게 된다.

• Receptive Field(수용 영역): 필터가 한 번에 '볼 수 있는' 입력 이미지의 공간적인 영역. 또는 출력 계층의 뉴런 하나에 영향을 미치는 입력 뉴런의 공간적인 영역.
  

• VGG는 메모리 사용량이 많은 편이며, 파라미터 개수도 AlexNet에 비해 많음.
  • 공간적 크기가 큰 초기 계층에서 많은 메모리를 사용하고, '완전 연결' 계층에서 많은 파라미터를 사용함.
• 모델 성능을 위해 앙상블 기법을 사용함.
• 마지막 부분의 FC-4096 계층은 매우 좋은 특징 표현 능력을 갖고 있음.

GoogLeNet

역시 22개의 깊은 계층을 가지고 있으며, 효율적인 계산을 위한 Inception Module 구조를 사용한다. 또한 파라미터 수를 줄이기 위해 완전 연결 계층을 사용하지 않았다. (AlexNet보다 파라미터가 12배 적음!)

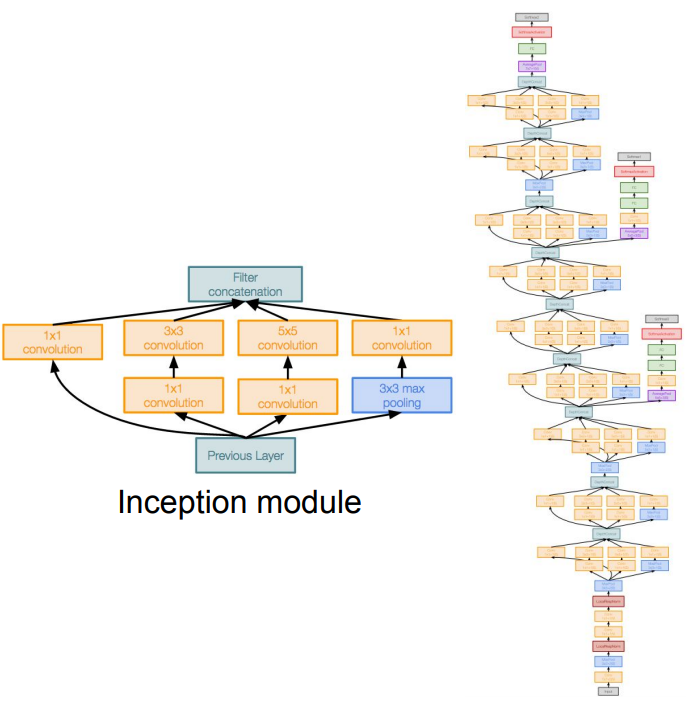
Inception Module에는 동일한 입력을 받는 서로 다른 다양한 필터들이 병렬로 존재한다. 이 서로 다른 필터에서 나온 출력들을 모두 깊이 방향으로 합쳐(Concatenate) 하나로 만든 후 다음 계층의 입력으로 전달한다.

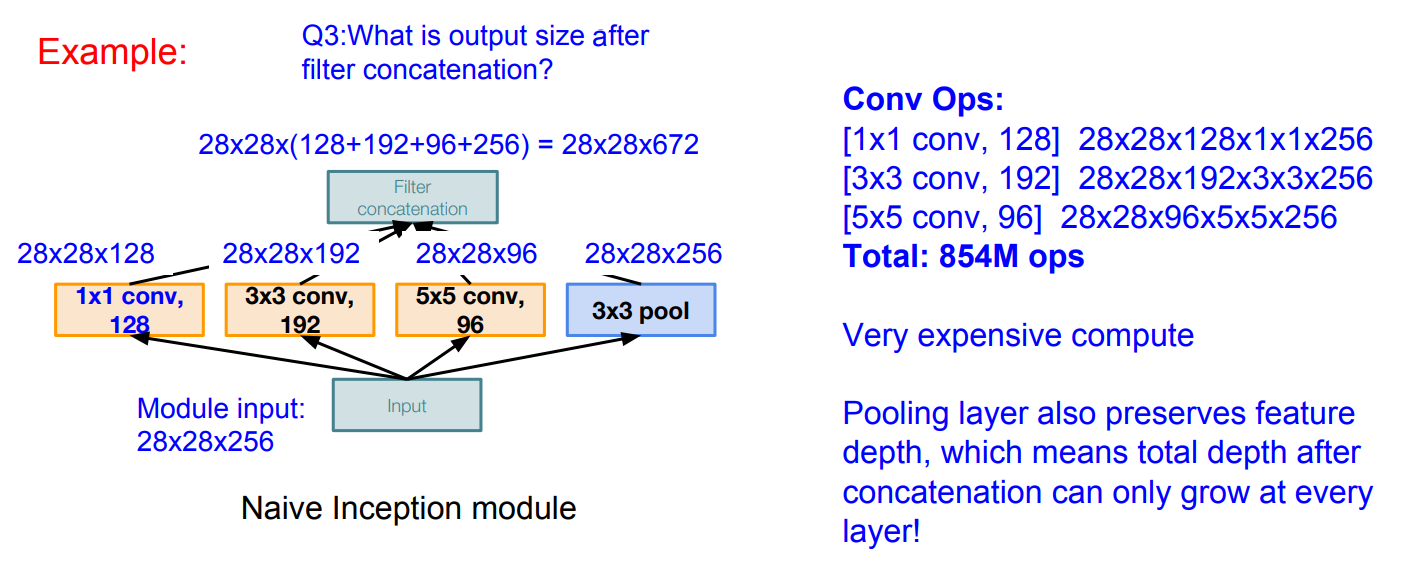
이때, 연산량이 지나치게 커지는 문제가 발생할 수 있다. 패딩과 스트라이드를 조절하여 입출력 간 공간적 크기는 유지하더라도, 여러 합성곱 연산 결과를 합치면서 출력 데이터의 깊이가 크게 늘어나게 된다. (풀링 계층 역시 깊이에 아무런 영향을 주지 못한다)

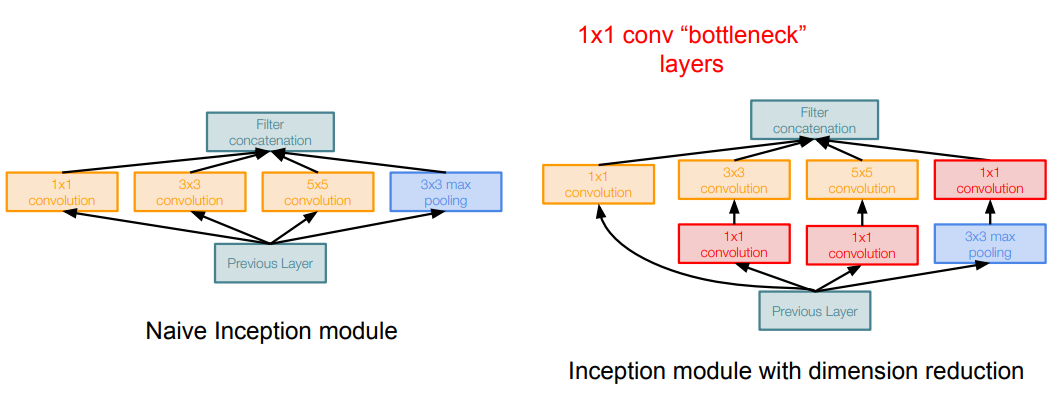
이에 대한 해결책으로 합성곱 연산 수행 전 '병목 계층'을 통해 입력을 더 낮은 차원으로 보낼 수 있다. 1×1 합성곱 연산이 입력의 공간적 크기는 그대로 유지하면서 깊이를 줄일 수 있다는 특성을 이용한 것이다.

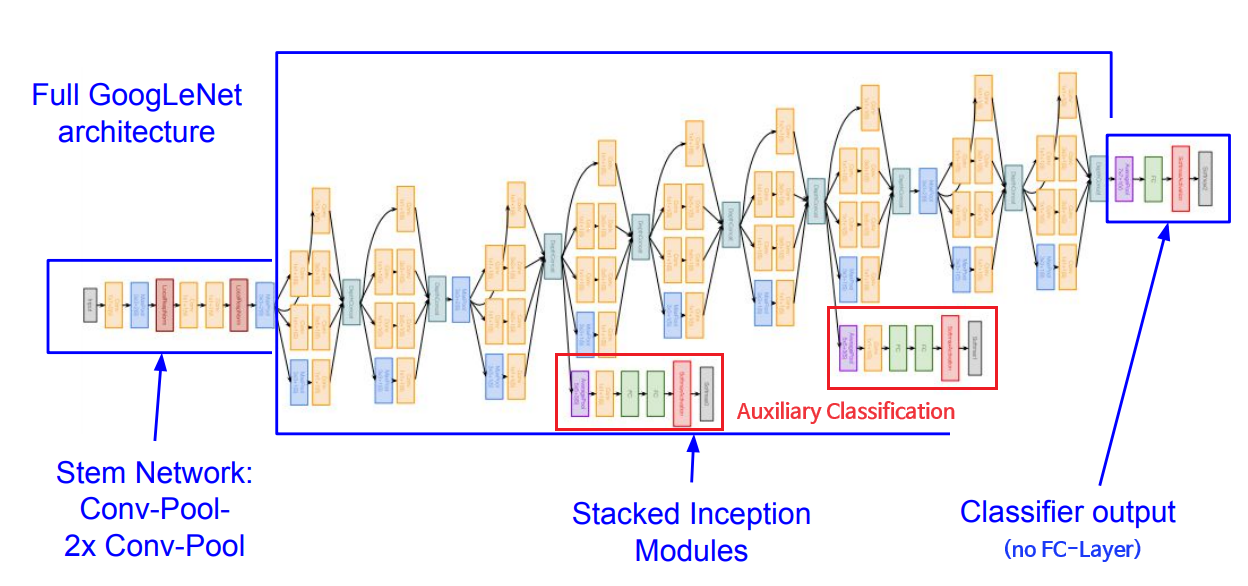
GoogLeNet의 전체 구조는 위와 같다. Auxiliary Classifier(보조 분류기)라 불리는 부분이 네트워크 중간 중간 존재하는데, 이는 깊은 네트워크 상에서 추가적인 그래디언트를 발생시켜 중간 계층의 학습을 돕기 위함이다.

ResNet

네트워크의 깊이가 급격히 깊어진 모델로, 무려 152개의 계층을 갖는 아키텍처이다.

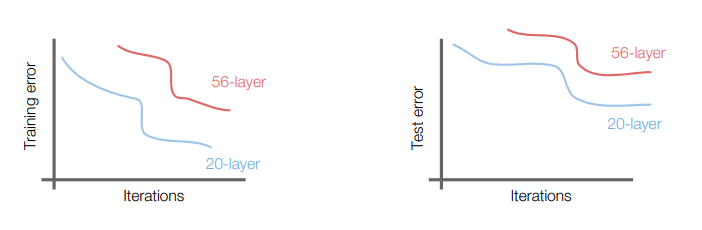
보통 CNN에서는 네트워크의 깊이와 성능이 반드시 비례하진 않는다. 계층이 깊어질수록 파라미터가 많아지므로 오버피팅을 일으켜서 그럴 것 같지만, 사실은 최적화가 어려워지는 것이 진짜 원인이다.

깊은 모델이 적어도 얕은 모델만큼의 성능을 갖도록 보장하는 방법은, 얕은 모델의 가중치를 깊은 모델의 일부 계층에 복사한 후 나머지 계층은 입력을 그대로 출력(Identity Mapping)하도록 구성하는 것이다.

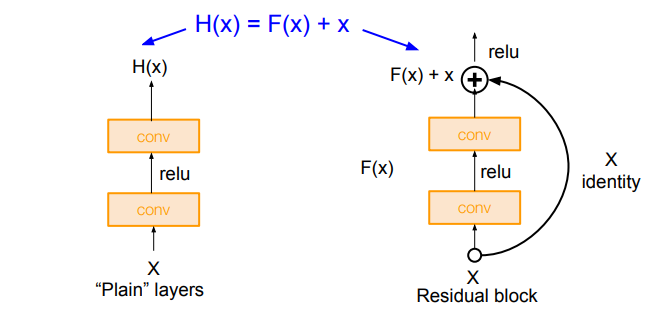
그 방법으로 ResNet은 각 계층이 '출력'이 아닌 '변화량', 즉 '잔차(Residual)'를 학습하도록 구성하며, 이러한 구조 단위를 'Residual Block'이라 한다.

위 그림에서 네트워크가 $H(x)$를 직접 배우는 대신, '이미 알고 있는 $x$에 얼마만큼의 $F(x)$를 더하고 빼야 할까?'를 배우는 게 더 쉽다는 것이 ResNet이 주장하는 가설이다.

• 만약 입력과 출력이 같아야 한다면(Identity Mapping), $F(x)$가 그냥 0이 되면 되므로 가중치를 0으로 만들기만 하면 됨!
• 역전파에서는 '+' 노드에 의해 나눠진 그래디언트가 현재 계층을 생략하고 곧장 이전 계층으로 흘러갈 수 있는 효과가 생기므로 그래디언트 소실 문제가 개선됨. (출력의 미분인 $F'(x) + 1$는 항상 0보다 크다)
• 이 부분에 대한 더 자세한 이해는 이 게시글을 참고하자.

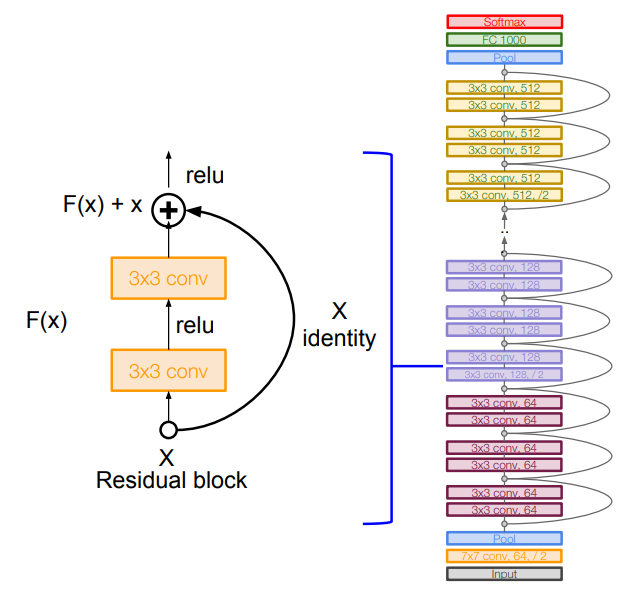
하나의 Residual Block은 2개의 3×3 합성곱 계층으로 구성되며, 이것을 150층까지 쌓아 올린다. 또한 주기적으로 필터의 개수를 두 배씩 늘리고, 처음 개수를 늘리는 계층에서는 스트라이드=2를 통해 Downsampling도 수행해 준다.

네트워크 끝에는 완전 연결 계층이 없으며 전역 평균 풀링 계층(GAP)을 통해 하나의 맵 전체를 평균 풀링하고, 마지막으로 1000개의 클래스 분류를 위한 노드가 붙는다.

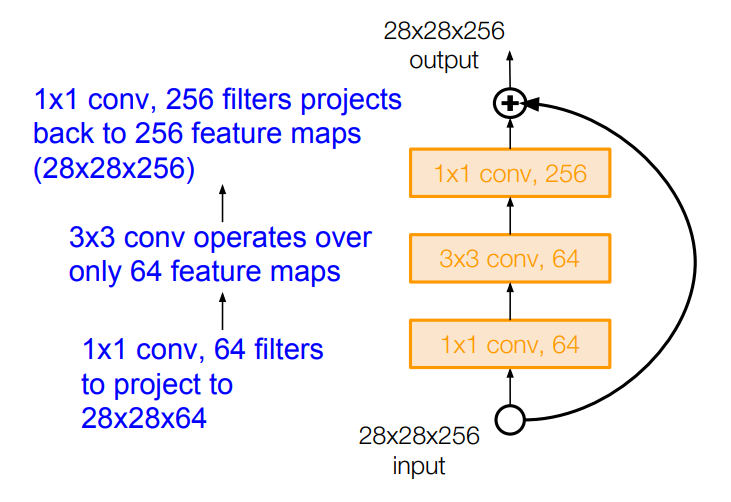
또한, 모델의 깊이가 50층 이상이라면 GoogLeNet처럼 병목 계층을 도입한다. 1×1 필터를 통해 3×3 필터 연산을 위한 입력의 깊이를 줄여주고, 출력 시 다시 1×1 필터를 통해 깊이를 늘려주는 구조이다.

ResNet의 기타 특징은 다음과 같다.

• 매 합성곱 계층 뒤에 배치 정규화 계층을 가짐.
• SGD + Momentum을 사용하며, 이에 적합한 Xavier/2 초깃값을 이용함.
• 학습률은 스케줄링을 통해 검증 에러가 줄어들지 않는 시점마다 조금씩 줄여줌.
• 미니 배치 크기는 256을 사용함.
• Weight Decay 기법을 사용하며, 드롭아웃은 사용하지 않음.

Comparing complexity

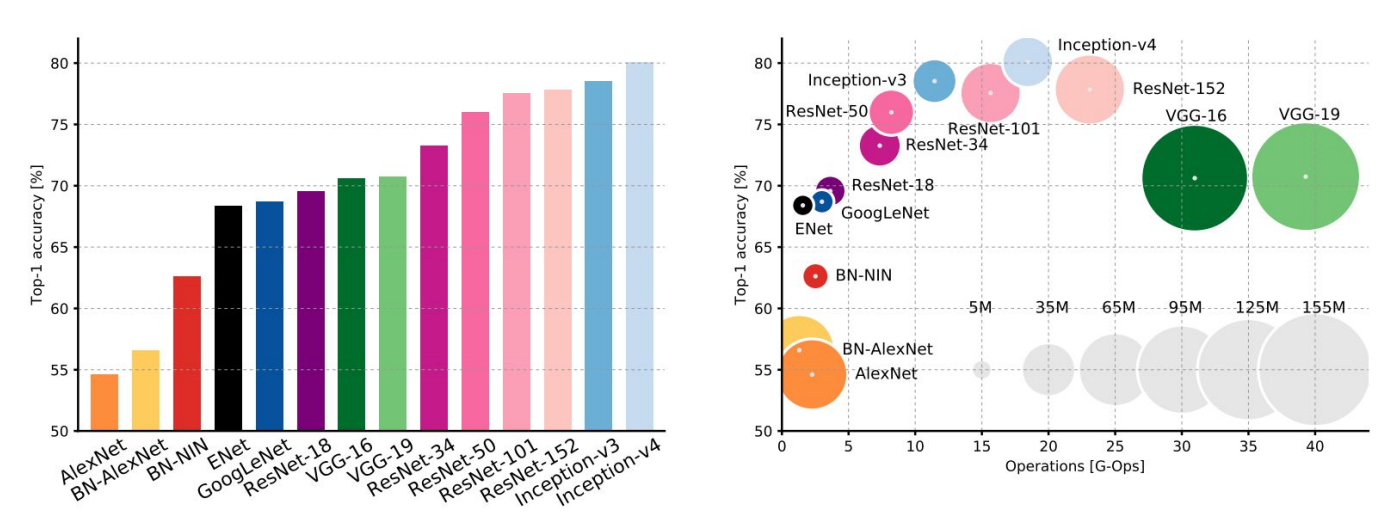
오른쪽 차트에서 Y축은 모델의 정확도, X축은 연산량, 원의 크기는 메모리 사용량을 뜻한다. 다양한 모델들의 성향 차이를 한눈에 볼 수 있다.

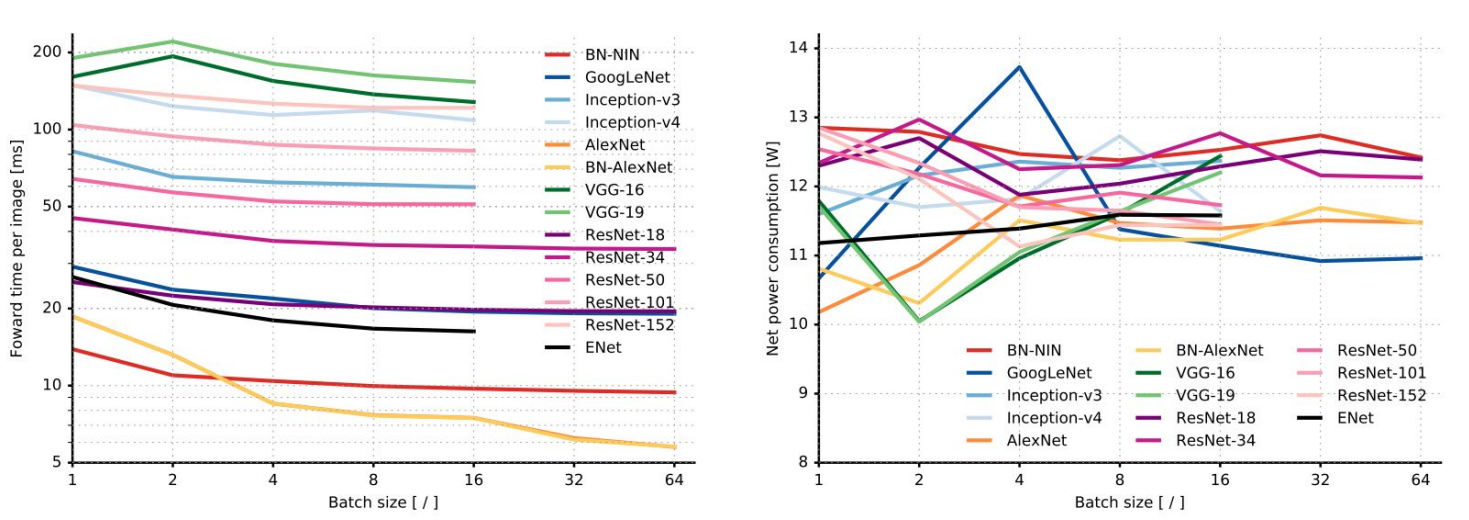
순전파 시 소요 시간과 전력 소모량도 소개되었다.

Other Architectures

• Network in Network(NiN)
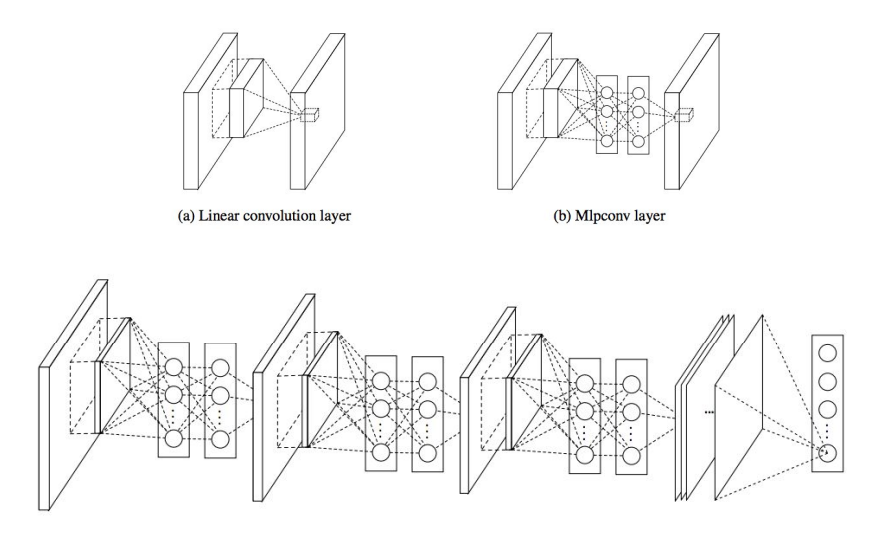  각 합성곱 계층 안에 MLP(Multi-Layer Perceptron)를 추가함으로써 복잡도를 올린다. GoogLeNet 이전에 '병목 계층' 개념을 정립한 구조이기도 하다.

• Improving ResNet
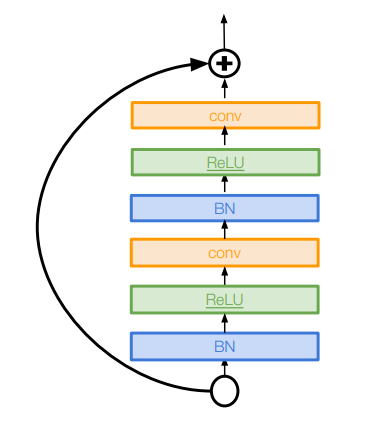  • 블록의 Direct 경로의 길이를 늘려서 정보들이 앞으로 더 잘 전달되고 역전파도 더 잘 이루어지도록 개선함.
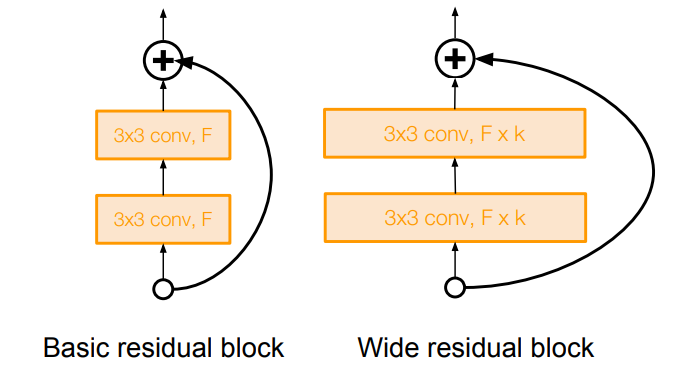  • 모델의 깊이 대신 Residual의 역할에 더 집중하여 Residual Block을 더 '넓게' 만듦. (필터의 수를 늘림) ⇒ 더 적은 수의 계층으로 더 높은 성능 & 계산 효율!
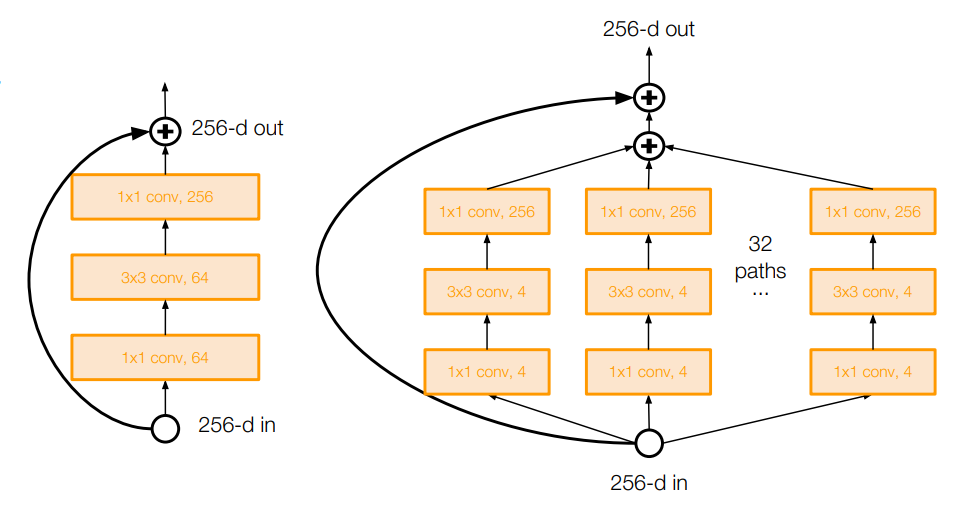  • ResNeXt: 역시 필터의 수를 늘리고 '다중 병렬 경로'를 추가하여 여러 개의 병목 계층들을 병렬로 묶음.
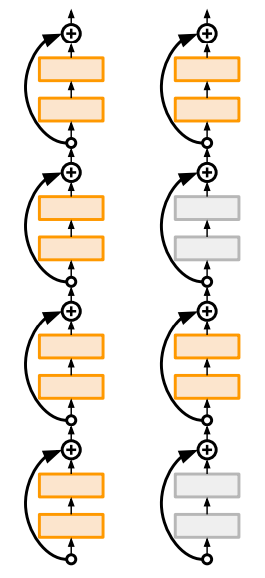  • 계층이 깊어질수록 발생하는 기울기 소실 문제를 해결하기 위해, 훈련 단계에서는 일부 계층을 제거하여 학습을 수행하고, 시험 단계에서는 전체 네트워크를 사용함. (드롭아웃과 유사!)

• Beyond ResNet
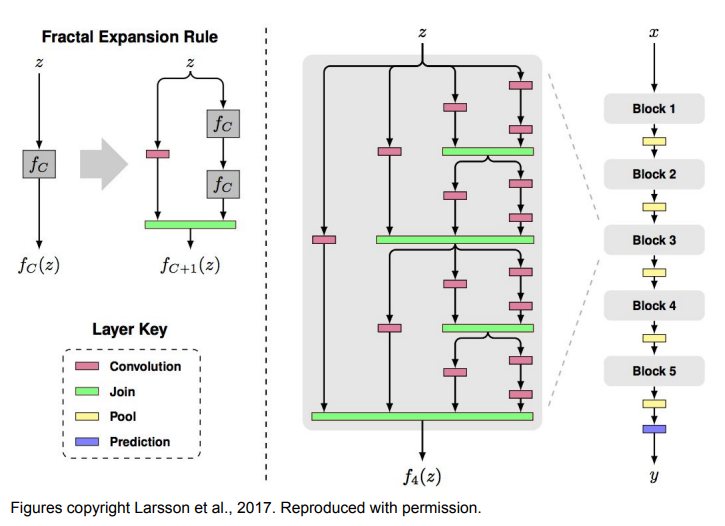  • FractalNet: ResNet의 Residual 개념을 부정함. 얕은 정보와 깊은 정보를 모두 잘 전달하도록 두 경로를 출력에 모두 연결하고, 드롭아웃과 유사한 방식으로 학습함.
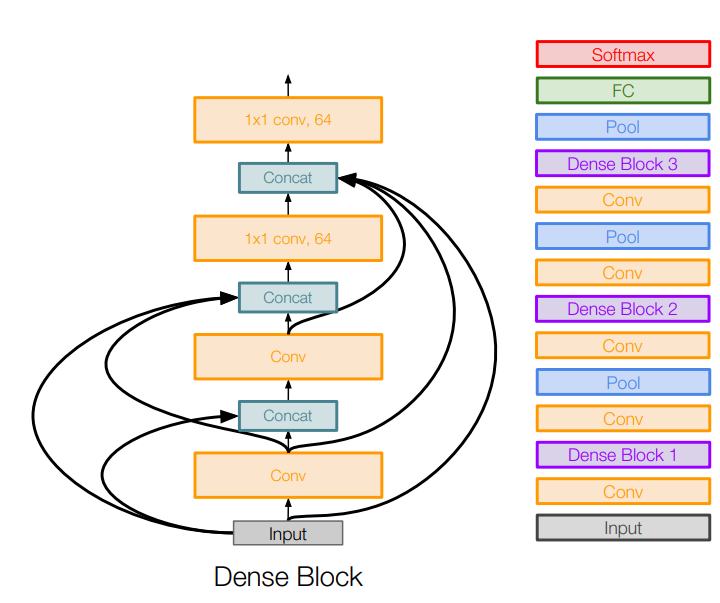  • 한 계층이 하위의 모든 계층과 연결(concat)되는 'Dense Block'이라는 단위를 이용하며, 이러한 구조가 기울기 소실 문제를 완화하고 특징을 더 잘 전달시킨다고 주장함.
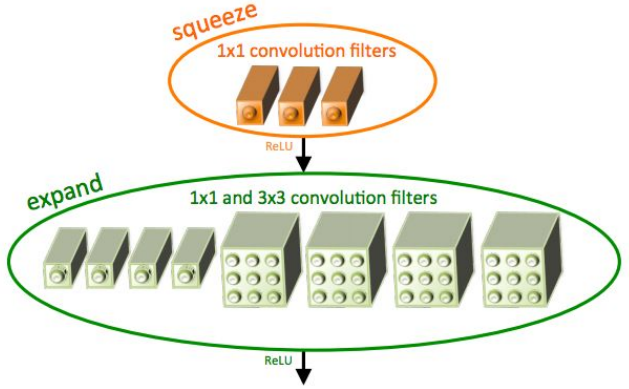  • SqueezeNet: 효율성에 초점을 맞춘 모델. AlexNet보다 500배 이상 작게 압축할 수 있음.

10. Recurrent Neural Networks

지금까지의 신경망은 하나의 입력에 대해 하나의 출력을 얻는 One-to-One 구조였다. RNN은 거기서 벗어나 네트워크가 더 다양한 입출력(가변 입력 & 가변 출력)을 다룰 수 있는 여지를 제공한다. (ex. 여러 문자로 이루어진 단어, 여러 단어로 이루어진 문장 등)

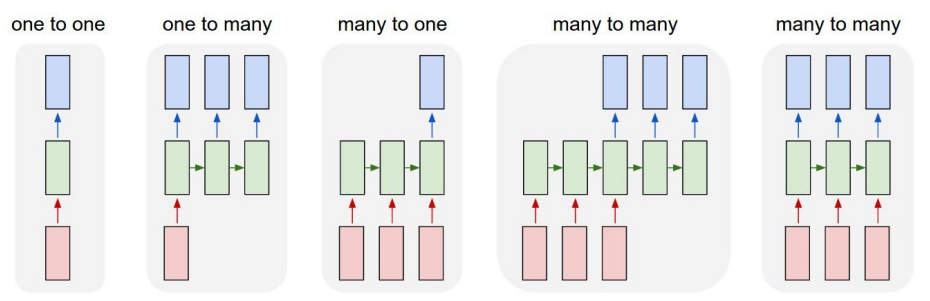
또한 기존처럼 입출력이 고정된 길이라고 해도 '가변 과정'이 따르는 경우 RNN이 유용하게 쓰인다. (ex. 순차적으로, 펜을 움직이듯이 이미지를 생성)

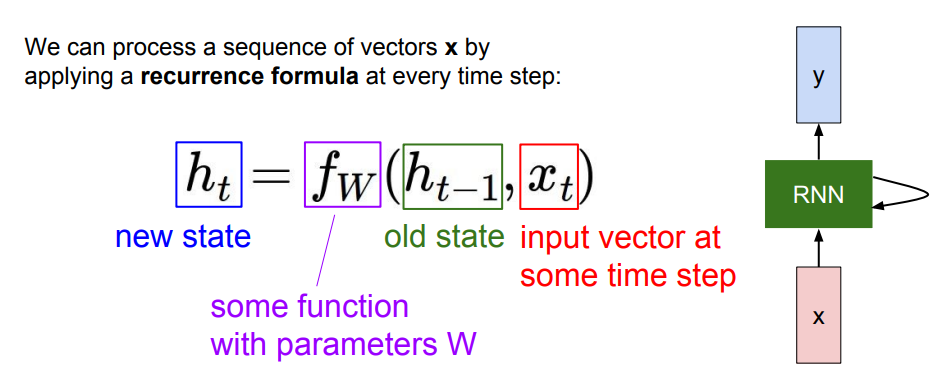
RNN은 작은 'Recurrent Core Cell'과 그 내부에 'Hidden State(은닉 상태)'를 가지고 있다. 은닉 상태는 RNN이 새로운 입력을 받을 때마다 매번 갱신되며, 이때 갱신 함수와 그에 대한 파라미터(가중치)는 매 스텝 동일하다. 출력 값은 은닉 상태를 입력으로 받는 완전 연결 계층으로부터 결정된다.

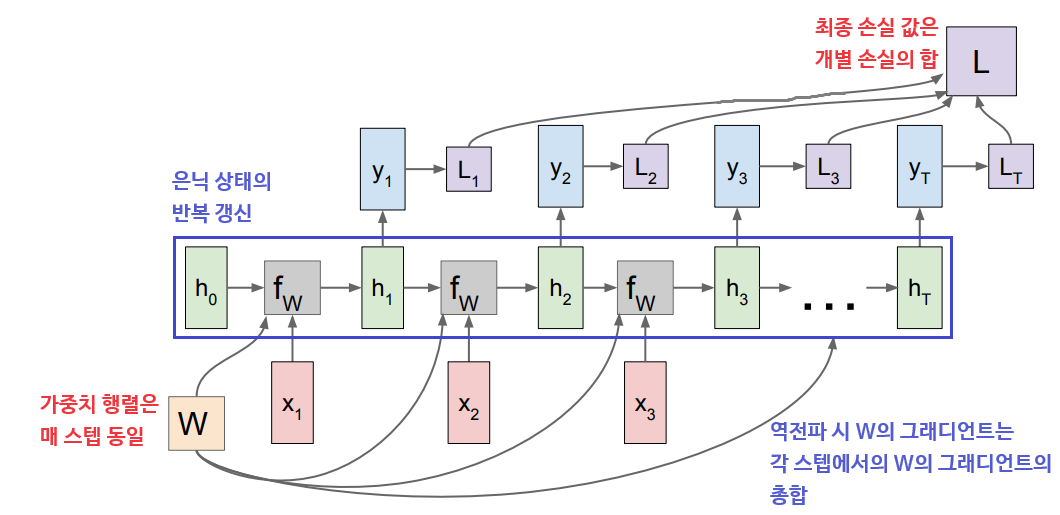
위 그림은 Many-to-Many 구조의 RNN을 계산 그래프로 나타낸 것이다. 은닉 상태가 '재귀적으로' 갱신되는 것을 풀어서(Unrolling) 표현하였다. (동시에 입력/출력되는 것으로 혼동하지 않도록 주의!)

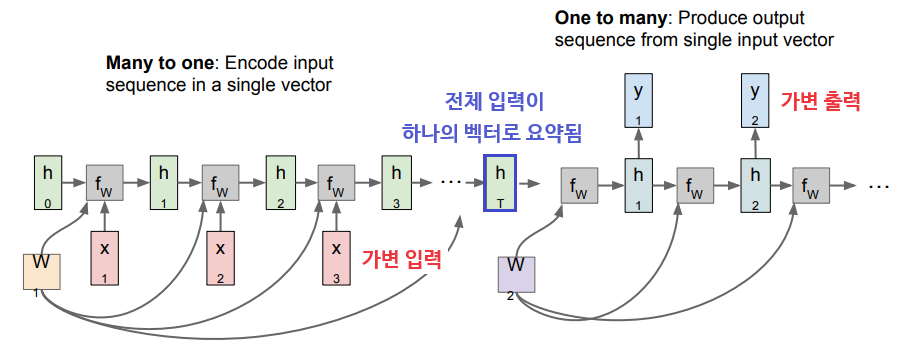
Many-to-One(인코더)과 One-to-Many(디코더)가 하나씩 결합한 Sequence-to-Sequence 구조도 있다. 가령, 한 언어의 문장을 다른 언어의 문장으로 번역하는 데에 쓰일 수 있다.

Character-Level Language Model Example

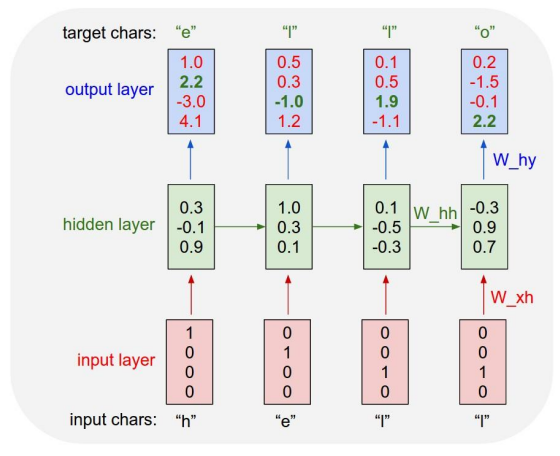
위 그림은 문자열을 읽은 후 현재 문맥에서 다음 문자를 예측하도록 학습시키는 과정을 나타낸 것이다.

벡터로 표현된 각 문자가 입력으로 들어올 때마다 RNN Cell을 거쳐 예측값을 내놓고, 정답과 비교하여 손실을 계산한다. 다음 문자가 들어오면 이전의 은닉 상태와 함께 새로운 은닉 상태를 만들어내고, 이를 통해 다시 적절한 값을 예측하는 것을 반복한다.

다양한 문장을 입력으로 하여 학습할수록 RNN은 점차 문맥 안에서 이전 문자를 참고하여 다음 문자를 예측하는 법을 배울 것이다.

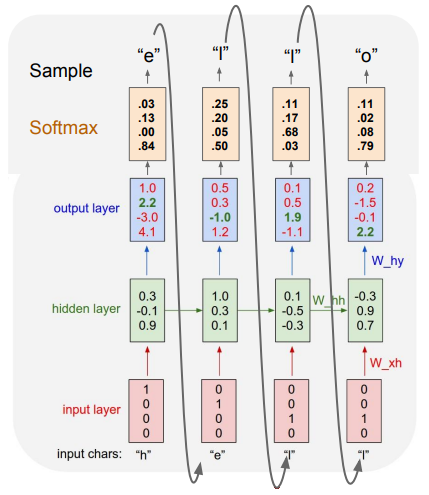
학습이 끝난 후 시험 단계에서는 문자 하나를 제공하여 모델이 스스로 적절한 문장을 생성해 내도록 한다. 각 입력에 대해 다음 문자를 예측한 점수를 소프트맥스를 통해 확률 분포로 만들고, 이 확률에 따라 문자를 뽑는다. (= '샘플링') 그리고 이렇게 선택된 문자를 다시 벡터로 만들어 다음 스텝의 입력으로 사용한다.

💡 왜 가장 높은 점수의 문자를 바로 택하지 않고 '샘플링' 하여 사용할까?

모델에서의 다양성을 얻을 수 있기 때문이다. 항상 같은 입력이 들어오더라도 첫 스텝에서 어떤 값이 샘플링되는지에 따라 다양한 출력을 얻을 수 있다.

Backpropagation Through Time

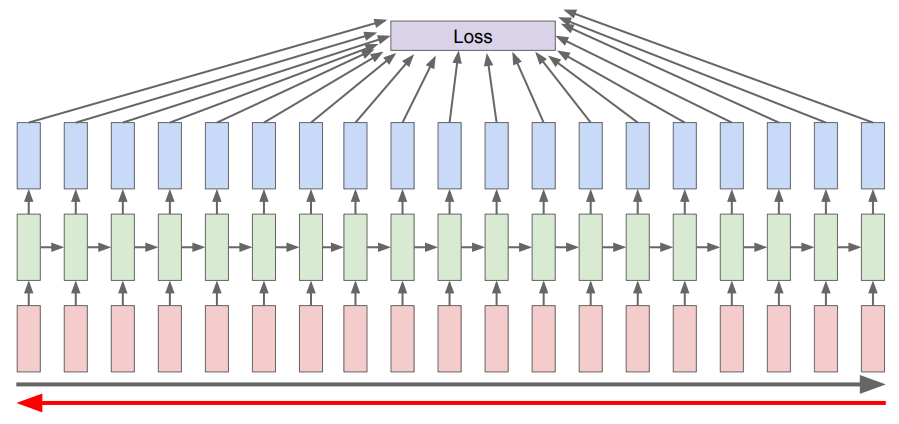
이러한 모델의 경우 각 시퀀스 스텝마다 출력값이 존재하며, 역전파에서도 전체 시퀀스를 가지고 손실을 계산해야 한다. 시퀀스가 길어질수록 그래디언트를 한 번 갱신하기까지의 시간이 점점 늘어날 것이다.

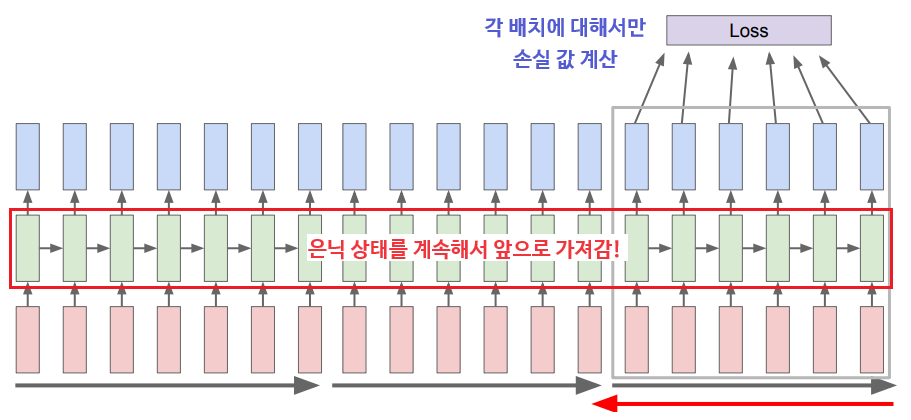
그래서 실제로는 'Truncated Backpropagation'을 통해서 역전파를 근사하는 기법을 사용한다.

스텝을 일정 단위로 자르고, 이 일부 시퀀스에 대해서만 순전파-손실 계산-역전파를 수행한 후, 갱신된 은닉 상태만을 가지고 다음 스텝을 처리하는 것을 반복하는 것이다. (SGD의 원리와 비슷!)

Image Captioning

RNN은 생각보다도 더 쉽게 구현할 수 있고, 어떤 문장이든 학습하여 그럴듯한 문장들을 생성할 수 있다. (문학, 수식, 코드 등등) 이는 단순히 다음 문자를 예측하라고만 지시하더라도, 모델이 학습 과정에서 시퀀스 데이터의 숨겨진 구조를 알아서 찾아 학습하기 때문이다.

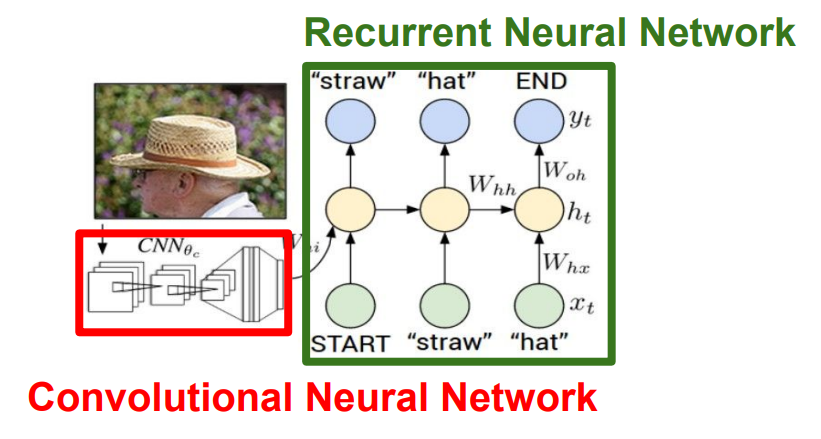
이미지 캡셔닝에도 RNN이 사용된다. '문장' 자체가 '가변 길이 데이터'이기 때문이다. 위 모델에서 CNN은 이미지를 받아서 요약된 정보가 담긴 벡터를 출력하고, RNN은 이 벡터를 초기 스텝으로 하여 캡션에 사용할 문자들을 하나씩 출력한다.

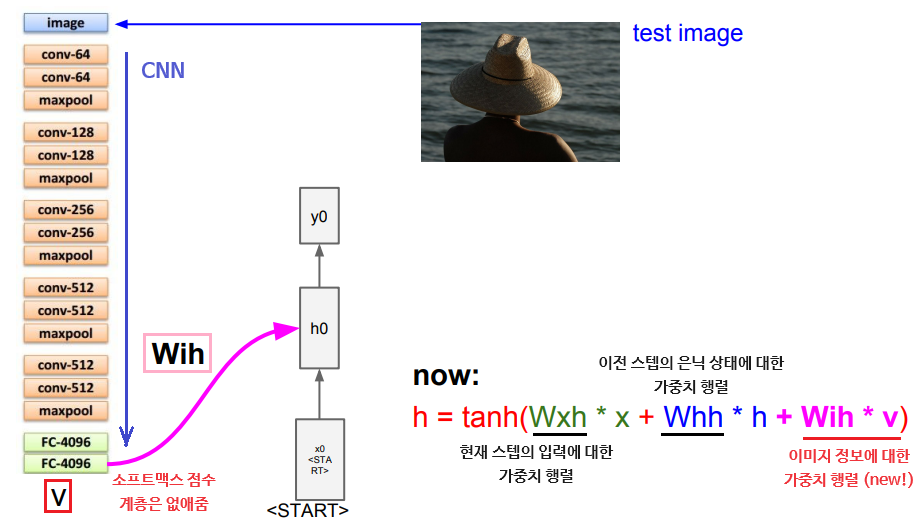
이미지 정보 벡터를 RNN의 입력으로 사용하는 방법은 새로운 가중치 행렬을 도입하는 것이다. 이렇게 되면 매 은닉 상태를 계산할 때마다 해당 이미지 정보가 추가된다.

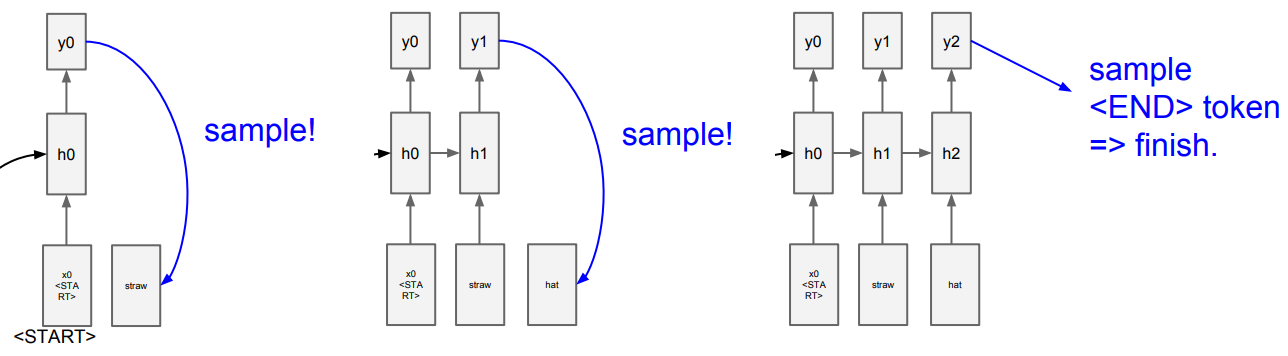
이후 '가능한 모든 단어들'에 대한 점수를 계산해서 확률 분포를 추정한 후 샘플링을 수행하여 다음 스텝의 입력으로 넣는 것을 반복하다가 <END> 토큰이 샘플링되면 샘플링을 중지한다.

• 이때 훈련 단계에서 모든 캡션의 종료 지점에 토큰을 삽입함으로써 '시퀀스의 끝에 토큰을 넣어야 한다는 것'을 학습하도록 해야 함.
• 위 모델은 지도 학습을 이용하므로 각 이미지에 대한 자연어 캡션이 있는 데이터셋을 사용해야 함.

• Attention Model: 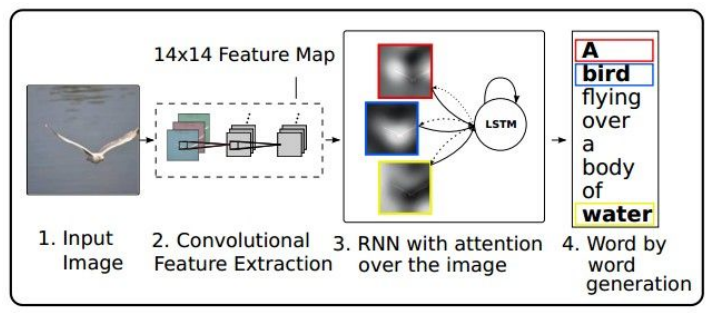이미지의 다양한 부분을 '집중해서' 볼 수 있는 모델. 캡셔닝 시 이미지에서 의미있는 부분에 집중하여 각 단어를 생성함.

• Visual Question Answering: 이미지와 질문을 건네면 적절한 답을 선택하는 문제. RNN으로 자연어로 된 질문을, CNN으로 이미지를 요약한 뒤 두 벡터를 조합하여 질문에 대한 분포를 예측함. 이때 위의 Attention 기법이 사용될 수 있음.

• Multi-Layer RNNs: 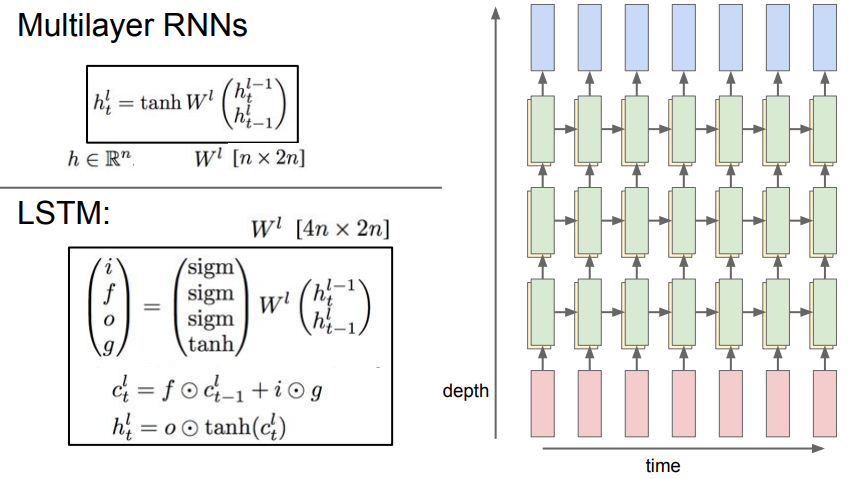하나의 RNN에서 생성한 은닉 상태 시퀀스를 다른 RNN의 입력 시퀀스로 넣어주는 식으로 여러 층을 쌓을 수 있으며, RNN 역시 계층이 깊어질수록 다양한 문제들에서 성능이 좋아짐. (주로 3~4층 정도를 사용)

RNN Gradient Flow

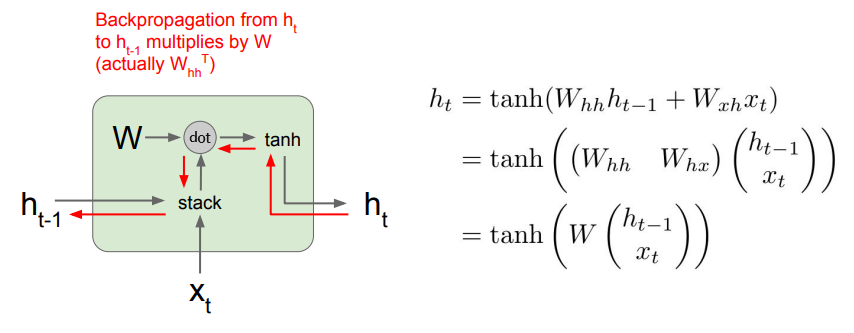
RNN에서 역전파 과정을 생각해 보면, 상류의 그래디언트가 RNN Cell을 한 번 통과할 때마다 (행렬곱 연산 노드에 의해) 가중치 행렬의 일부와 곱해지게 된다.

RNN은 Cell을 재귀적으로 돌면서 은닉 상태를 갱신하는 구조이므로, 역전파가 길어질수록 많은 가중치 행렬들이 곱해질 것이다. 즉, 가중치 행렬의 특이값(Singular Value)이 1보다 크다면 그래디언트가 점차 폭주(Exploding)할 것이고, 반대로 1보다 작다면 소멸(Vanishing)될 것이다.

• Gradient Clipping: 계산된 그래디언트의 L2 Norm이 최대 임계값을 넘지 않도록 조정하는 기법. 그래디언트 폭주 문제를 해결할 때 사용됨.

Long Short Term Memory (LSTM)

RNN의 그래디언트 폭주 및 소멸 문제를 완화하기 위해 개선된 버전이다. Gradient Clipping 등의 휴리스틱한 기법을 쓰지 않고도 그래디언트가 잘 전달되도록 설계되었다.

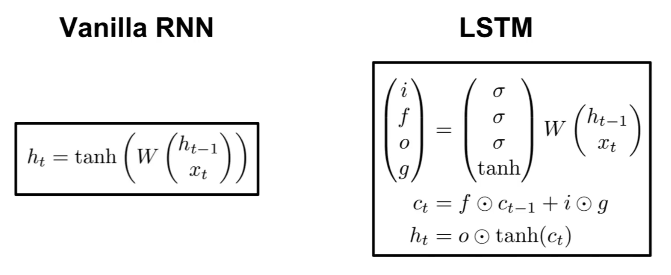
LSTM에서는 각 셀마다 내부적으로 2개의 상태를 갖는데, 하나는 기존의 '은닉 상태'이고, 다른 하나는 'Cell State(셀 상태)'이다. 또한 이 셀 상태를 업데이트하기 위해 4개의 게이트($i$, $f$ ,$o$, $g$)를 추가로 갖는다.

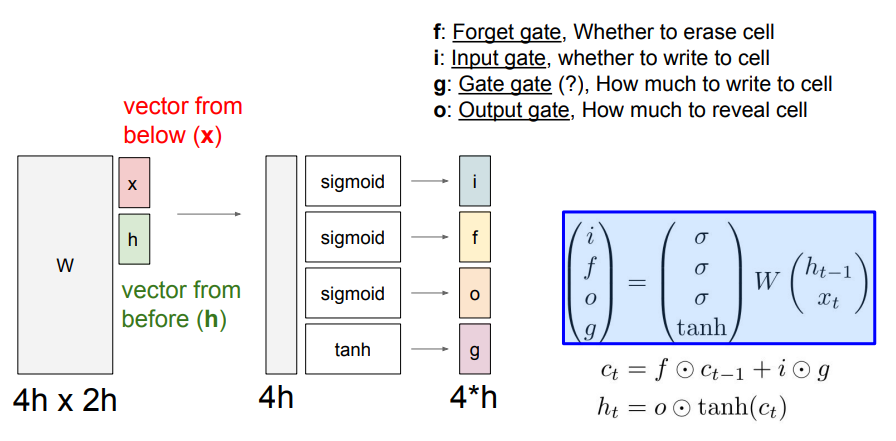
LSTM은 매 입력으로 이전 은닉 상태 $h_{t}$와 현재 입력 $x$를 받아 쌓아놓고 커다란(4개 분량의) 가중치 행렬과 곱해준다. 이로부터 4개의 게이트를 계산한 후, 이 값을 이용해 셀 상태 $c_{t}$와 은닉 상태 $h_{t}$를 순차적으로 계산한다.

• Input Gate: 셀에서의 입력 $x$에 대한 가중치. (Sigmoid 사용)
• Forget Gate: 이전 스텝의 셀 상태를 얼마나 망각할지에 대한 가중치. (Sigmoid 사용)
• Output Gate: 현재 스텝의 셀 상태를 얼마나 밖에 드러낼지에 대한 가중치. (Sigmoid 사용)
• Gate Gate: 입력 셀을 얼마나 포함시킬지에 대한 가중치. (tanh 사용)

위 게이트의 값은 모두 스칼라 값이며, 시그모이드 또는 tanh을 사용하므로 [0, 1] 또는 [-1, 1]의 값을 갖는다. 자세한 계산 과정은 밑의 그림을 참고하자.

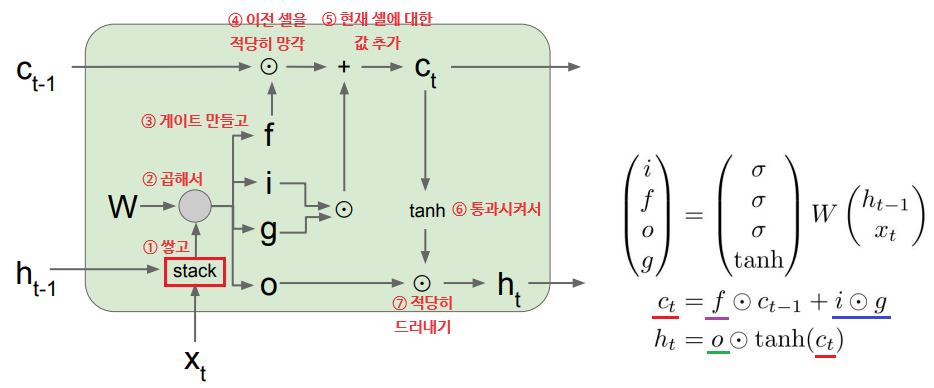
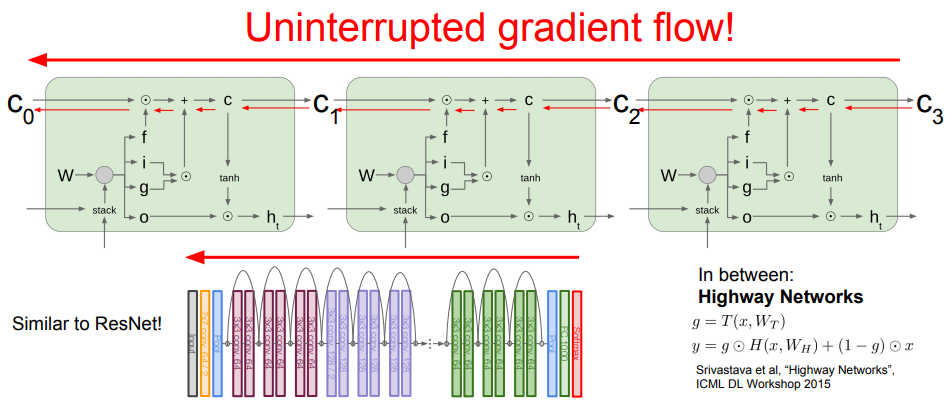
한편, LSTM의 각 셀에서 셀 상태에 대한 역전파를 생각해 보면 상류의 그래디언트가 Forget Gate와 한 번만 곱해지며 통과한다는 것을 알 수 있다.

이때의 곱연산은 '행렬의 전체 내적'이 아닌 '요소별 곱셈'이므로 더 가볍고, 매 스텝마다 동일한 가중치가 아닌 '새로운 값(= Forget Gate)'과 곱해지므로 기울기 폭주/소실 문제가 완화된다.

또한, 최종 은닉 상태 $h_{t}$에서 가장 첫 셀 상태 $c_{0}$까지 역전파를 보낼 때에도 기존 RNN과 달리 tanh 함수를 단 한 번만 거치면 된다.

이는 ResNet에서 역전파를 더 수월하게 전달할 수 있도록 일종의 '고속도로'를 두는 것과 비슷하다.

• GRU(Gated Recurrent Unit): LSTM을 보다 가볍게 개선한 버전.

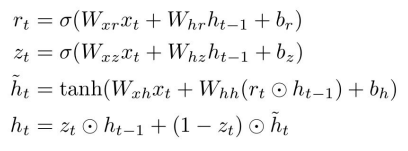
11. Detection and Segmentation

지금까지의 Image Classification 문제는 하나의 이미지를 입력받아 그에 맞는 적절한 클래스로 분류하는 문제였다. 이 외에도 딥러닝을 이용하여 풀 수 있는 문제들이 여럿 존재한다.

Semantic Segmentation

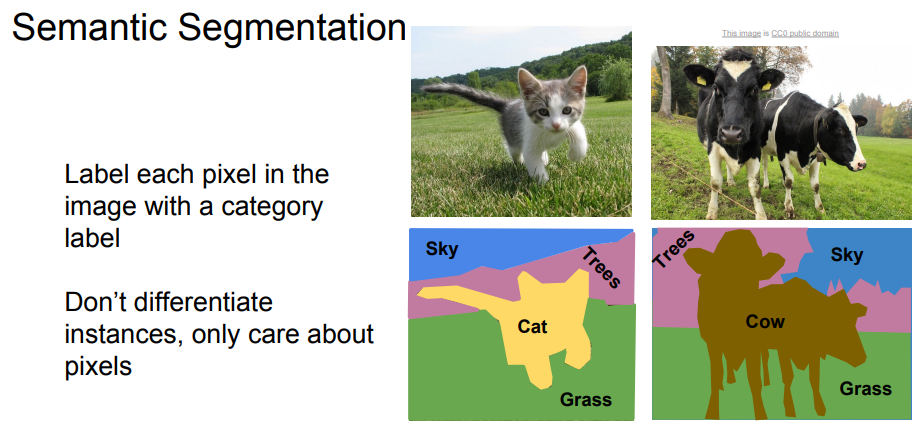
이미지를 입력으로 받아서 출력으로 이미지의 모든 픽셀마다 카테고리를 분류하는 문제이며, 개별 객체는 구분하지 않는다. 대략 다음과 같은 방법들을 생각해 볼 수 있다.

• Sliding Window: 입력 이미지를 매우 작은 단위로 쪼갠 뒤, 각 영역마다 클래스를 분류함. 기존의 이미지 분류기를 개별적인 단위마다 적용하는 것.
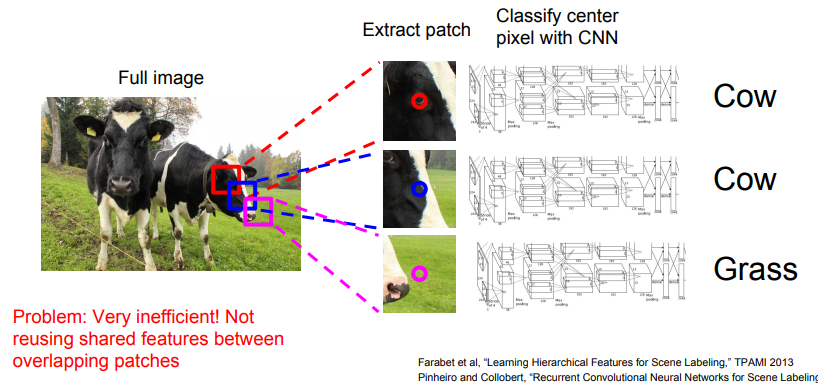
  • 당연히 매우 비효율적인 방법이며, 인접한 영역끼리 공유하는 특징이 있을 수 있음.

• Fully Convolutional Network: 완전 연결 계층 없이 합성곱 계층으로만 이루어진 네트워크. 훈련을 위해 이미지의 모든 픽셀마다 레이블이 필요하며, 각 픽셀의 예측값을 통해 손실(Cross-Entropy)을 계산함. 한 번에 모든 픽셀을 예측할 수 있음.
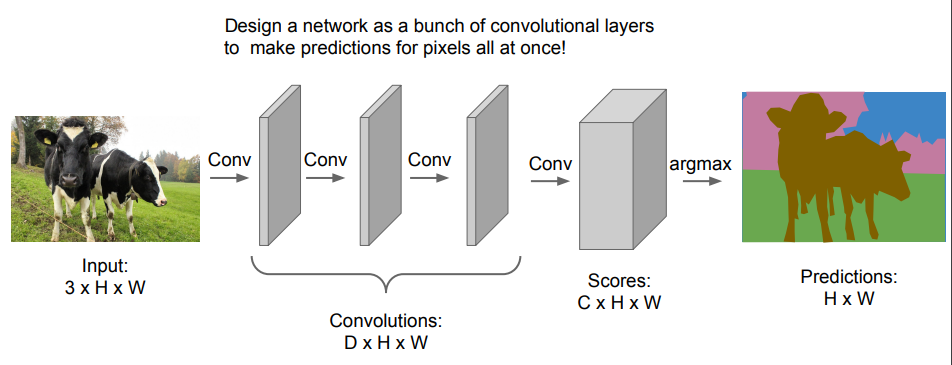
  • 하지만 입력 이미지의 공간적 크기를 계속 유지시켜야 하므로 비용이 매우 큼.
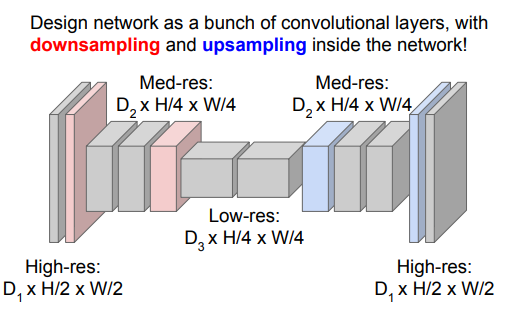
  • 따라서 이런 식으로 다운샘플링과 업샘플링을 순차적으로 적용하는 방식을 이용함.

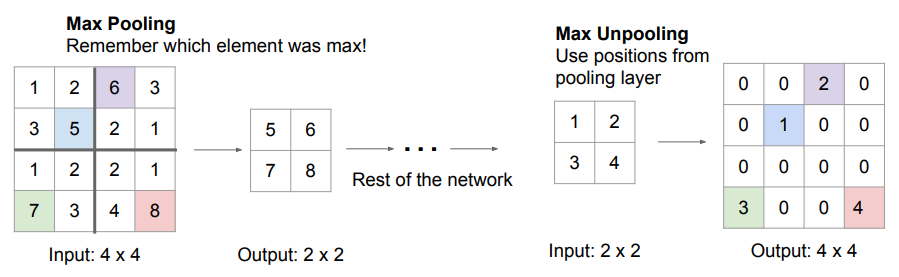
이미지를 업샘플링하기 위한 방법 중 하나는 Unpooling을 이용하는 것이다.

• Nearest Neighbor Unpooling: 출력의 Receptive Field 만큼 원본 값을 모두 채워 넣음.
• Bed of Nails Unpooling: 한 위치에만 값을 복사하고 다른 곳에는 모두 0을 채워 넣음.
• Max Unpooling: Max Pooling 적용 시 선택됐던 원소의 위치에만 값을 복사하고 다른 곳에는 모두 0을 채워 넣음. 풀링 과정에서 잃어버리는 공간 정보를 조금 더 잘 유지하는 효과가 있음.

반면, Transpose Convolution은 Unpooling처럼 고정된 함수가 아닌 '학습 가능한' 방법이다. 즉, 특징 맵을 업샘플링할 때 어떤 방식으로 해야 할지를 학습한다.

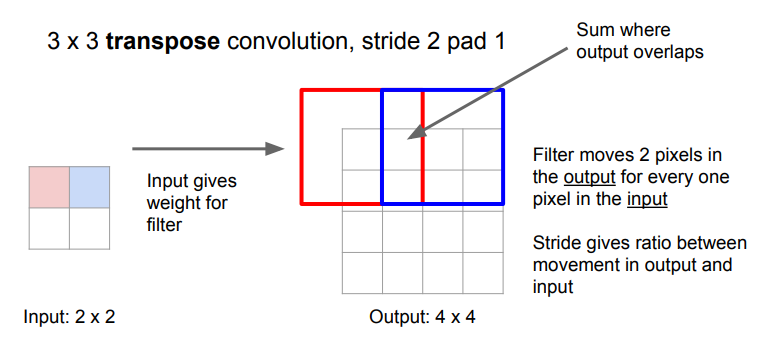
기존 합성곱 연산에서 출력의 크기가 입력의 크기로부터 스트라이드의 비율만큼 줄어드는 것처럼, Transpose Convolution에서는 반대로 각 입력을 가중치(스칼라 값)로써 필터의 모든 요소에 곱한 결과를 스트라이드만큼 이동하면서 출력으로 결정한다. 이때 출력에서 서로 겹치는 부분은 단순히 더해주면 된다.

• Transpose Convolution은 다양한 이름으로 불린다: Deconvolution, Upconvolution, Fractionally Strided Convolution, Backward Strided Convolution

Classification + Localization

이미지를 특정 클래스로 분류함과 동시에, 이미지 내에서 해당 클래스의 객체가 '어디에 있는지'를 찾아 사각형 테두리(Bounding Box, BBox)로 표시하는 문제이다. 여기서는 이미지 내에서 찾을 객체가 단 하나만 있다고 가정한다.

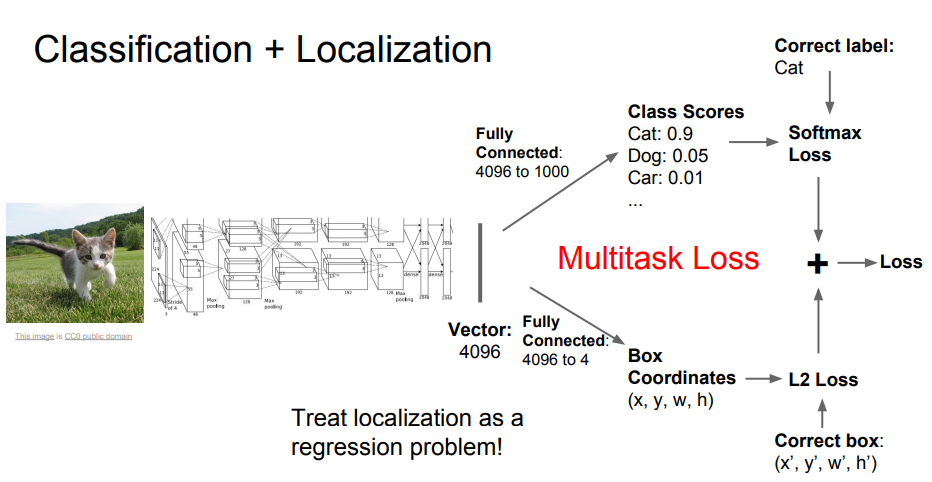
기존의 이미지 분류기에서 입력 이미지에 대한 클래스별 점수뿐 아니라 '객체의 위치와 크기'를 가리키는 출력을 위한 완전 연결 계층을 추가한다. 출력이 두 개이므로 손실 함수도 두 개가 필요하며, 클래스별 점수는 소프트맥스로, BBox의 예측값은 L2 Loss로 손실을 계산한다. 이후 하이퍼파라미터를 통해 두 손실의 가중치 합을 구해 최종 손실을 계산한다.

• 이때 문제는 '완전 지도 학습'을 가정하므로, 훈련 시 이미지별 라벨링뿐 아니라 이미지 내 객체의 BBox에 대한 정보도 같이 제공해야 한다.

• Human Pose Estimation: 사람 이미지를 입력으로 받아 각 관절의 위치, 즉 사람의 포즈를 예측함.

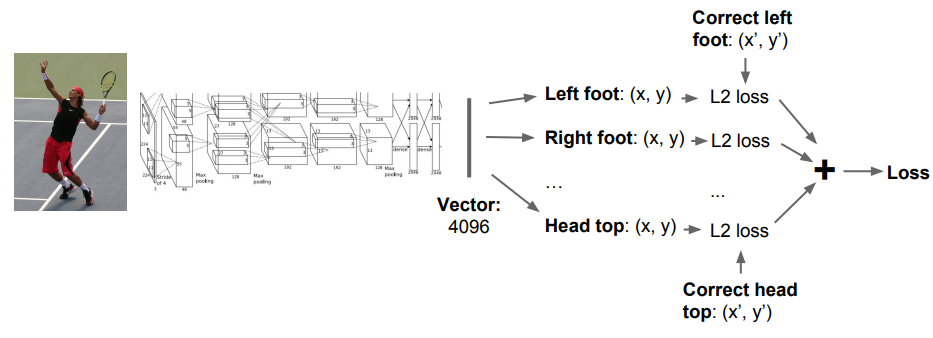
💡 'Regression(회귀) Loss'란?

Cross Entropy나 Softmax처럼 Classification(분류) Loss가 아닌 손실 함수. L2, L1, Smooth L1 등이 있음. (출력이 카테고리별 값이냐, 연속적인 값이냐)

Object Detection

입력 이미지에 나타나는 객체들의 BBox와 해당하는 카테고리를 예측하는 문제. 카테고리 수는 고정되어 있으나 각 이미지에 객체가 몇 개나 있을지는 미리 알 수 없다.

• Sliding Window: 입력 이미지를 다양한 영역으로 쪼개고 각각을 CNN에 넣는 방법. '아무 객체도 없음'을 뜻하는 '배경' 카테고리를 추가해야 함.
  • 영역을 추출하기 위한 경우의 수가 너무 커짐. 객체가 몇 개일지, 어디에 존재하며 크기는 어느 정도일지를 알 수 없기 때문.
• Region Proposals: 전통적인 신호처리 기법(Selective Search 등)을 사용하여 객체가 있을법한 여러 BBox 후보들을 제공받은 후, 이를 CNN의 입력으로 함.

Region Proposals은 R-CNN이라는 논문에서 실제로 사용된 방법이다.

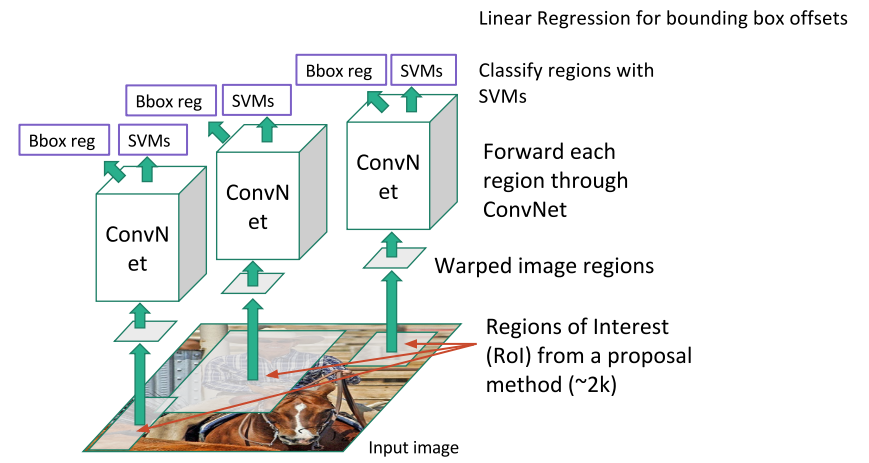
R-CNN에서는 먼저 입력 이미지에서 Selective Search를 통해 2000개의 후보(ROI)를 얻어낸 후, 각 ROI의 크기를 동일하게 변환하여 CNN에 넣는다. CNN에서 출력된 특징 맵은 SVM을 통해 분류하며, 이때 다소 부정확할 수 있는 BBox를 보정하기 위한 오프셋 값 4개도 예측한다.

• 문제점: 이미지 한 장당 2000개의 ROI가 만들어지고, 이 ROI들 각각이 CNN의 입력으로 들어가므로 계산 비용도 높고 속도도 상당히 느림.

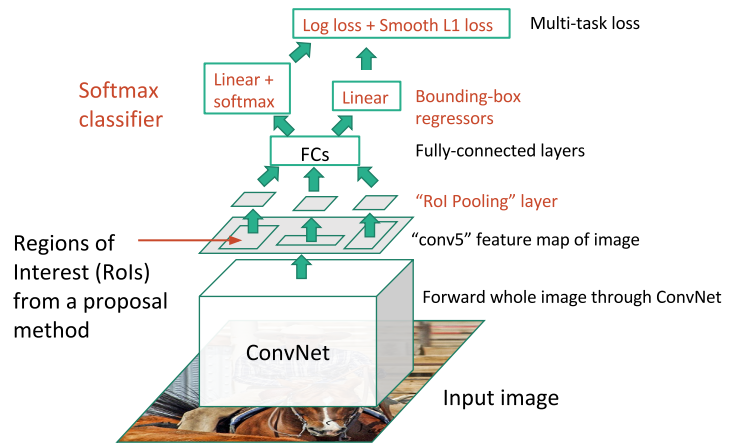
이 문제들을 대부분 개선한 Fast R-CNN은 각각의 ROI가 아닌 전체 이미지에 CNN을 수행하여 고해상도의 특징 맵을 얻고, 이 특징 맵에서 ROI를 선택한다. 이후 ROI 풀링 계층에서 각 ROI의 크기를 동일하게 조정하고, 완전 연결 계층의 입력으로 넣어서 분류 점수와 오프셋을 계산한다. 최종 손실은 두 값에 대한 손실을 합쳐 계산하여 전체 네트워크를 동시에 학습하도록 한다.

• 훈련 단계에서는 Fast R-CNN이 일반 R-CNN보다 10배 정도 빠르며, 시험 단계에서는 20배 이상 빠르다. 이때 2000개의 ROI를 계산하는 시간이 대부분을 차지한다.

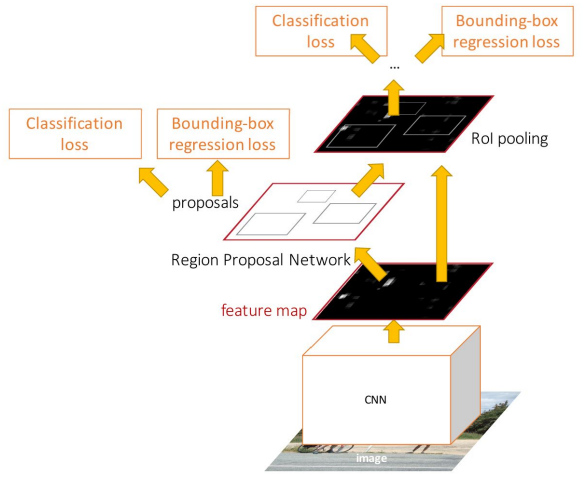
또 한 번 발전한 Faster R-CNN은 별도의 Region Proposal Network(RPN)를 두어, 네트워크가 CNN에서 나온 특징 맵으로부터 직접 ROI을 예측하도록 한다. 나머지 과정은 기존 Fast R-CNN과 동일하며, 마지막에 4개의 손실을 동시에 계산한다.

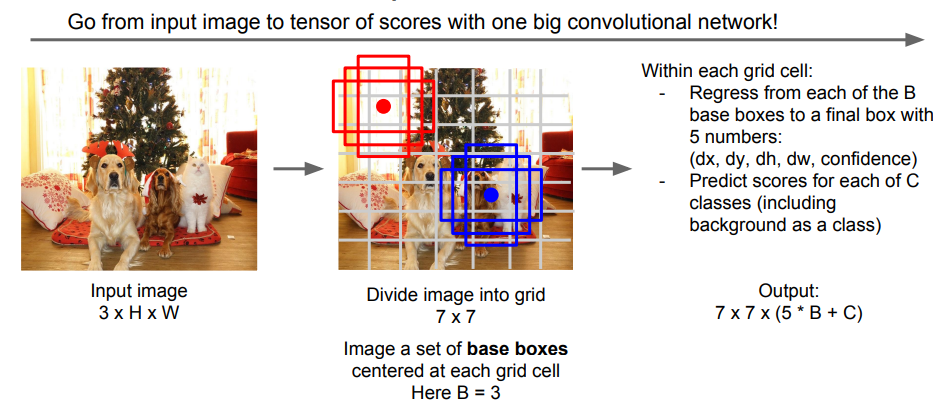
한편, 각각의 ROI를 독립적으로 계산하는 R-CNN 계열과 달리, YOLO와 SSD는 이들을 하나의 회귀 문제로 푸는 방법이다. (= Single-Shot 계열)

여기서는 입력 이미지를 적당히 큰 그리드 단위로 나누고, 각 셀마다 3개 이상의 Base BBox를 둔다. 그리고 이 각각의 Base BBox에 대해 오프셋과 분류 점수 예측을 수행한다. 출력은 3차원의 텐서가 되며, 이를 거대한 CNN으로 한 번에 학습한다.

Instance Segmentation

입력 이미지가 주어졌을 때, 이미지 내에 존재하는 여러 개의 객체를 찾고 픽셀 단위로 분할하는 문제이다.

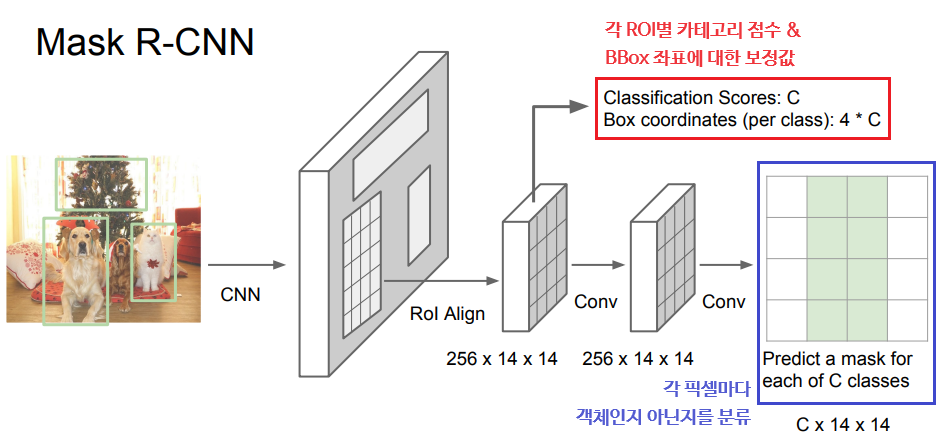
Mask R-CNN은 Faster R-CNN처럼 입력 이미지가 CNN과 RPN을 거치도록 한 후, 특징 맵에서 ROI를 가져오고 각 ROI마다 분할 마스크를 예측하도록 한다. Semantic Segmentation과 Object Detection 문제에서 쓰인 방법들이 고루 이용되었다.

• 사람의 관절에 대한 정보만 추가하면 Pose Estimation도 가능하다! 즉, Mask R-CNN 하나로 위에 나온 대부분의 문제들을 해결할 수 있다.

12. Visualizing and Understanding

CNN이 정확히 '어떻게' 동작하는지, 구체적으로 '어떤 것'을 보고 있는지를 시각화하여 이해를 높여보자.

Visualizing First & Last Layer

CNN의 첫 번째 계층의 필터에서는 윤곽선이나 보색 같은 패턴들이 명확히 관찰된다. 하지만 두 번째 계층의 필터부터는 '현재 계층의 출력을 최대화시키는 앞 계층의 출력 패턴이 무엇인지'를 가리키게 되므로 시각적으로 의미를 파악하기 어려워진다.

한편, 마지막 은닉층은 각 이미지에서 추출된 특징 벡터들을 저장하고 있다. 이를 '픽셀 공간'이 아닌 '특징 공간'에서 Nearest Neighbors 알고리즘으로 가장 가까운 이미지를 계산해 보면, '픽셀 값의 차이는 크더라도 의미적인 특징이 유사한' 이미지가 나타나는 것을 볼 수 있다.

PCA와 비슷한 t-SNE(t-distributed Stochastic Neighbor Embedding)라는 기법을 이용해 4096차원의 각 특징 벡터들을 2차원으로 압축시킨 후, 각 값을 좌표로 하여 2차원 특징 공간에 상응하는 이미지를 위치시키면, 학습된 특징 공간의 기하학적 형태를 대략적으로 파악할 수 있다.

💡 PCA란?

주성분 분석(Principal Component Analysis)의 약자로, 고차원 데이터를 저차원 데이터로 압축시키는 기법을 말한다.

Visualizing Activations

중간 레이어의 가중치 자체는 시각적으로 해석하기 어렵지만, 대신 레이어의 최종 출력인 Activation Map(특징 맵)을 이용해 볼 수 있다.

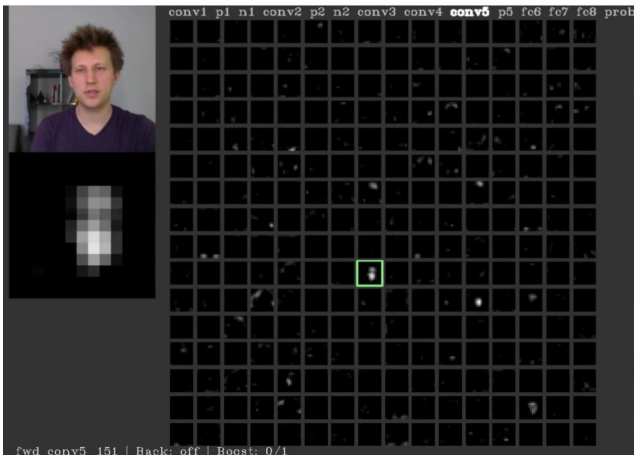• AlexNet의 conv5 레이어의 출력은 128×13×13 차원의 텐서이다. 이를 13×13 크기의 흑백 이미지 128장으로 잘라서 시각화할 수 있다. (중앙 쪽 출력에서 사람의 얼굴과 비슷한 형체가 보인다)

• 하나의 특징 맵에 대해, 수많은 이미지를 CNN에 통과시키면서 '어떤 이미지가 해당 특징 맵을 최대로 활성화시키는지'를 확인하는 방법도 있다.
  • 우측 사진은 좌측보다 더 깊은 레이어에서의 활성을 확인한 사진이다. 더 넓은 Receptive Field를 보면서 더 큰 구조를 찾고 있다.

Occlusion Experiments

한편, 입력 이미지의 임의의 위치에 가림막을 붙인 뒤 CNN을 통과시키면서 '분류를 제대로 예측할 확률'이 얼마나 떨어지는지를 관찰해 보면, '입력 이미지의 어떤 부분이 분류를 결정짓는 데에 중요하게 작용하는지'를 짐작할 수 있다.

Saliency Map

만약 픽셀 단위로 이를 판단하고 싶다면, 입력 이미지의 각 픽셀들에 대하여 예측한 클래스 점수의 그래디언트를 계산하는 방법을 쓴다. (= '어떤 픽셀의 값을 살짝 바꾸었을 때, 클래스 점수를 얼마나 변화시키는가?')

추가로 Saliency Map은 (물론 기존 방식에 비해 성능이 떨어지긴 하지만) Semantic Segmentation 문제를 푸는 데에도 이용할 수 있다!

Intermediate Features (via Guided Backprop)

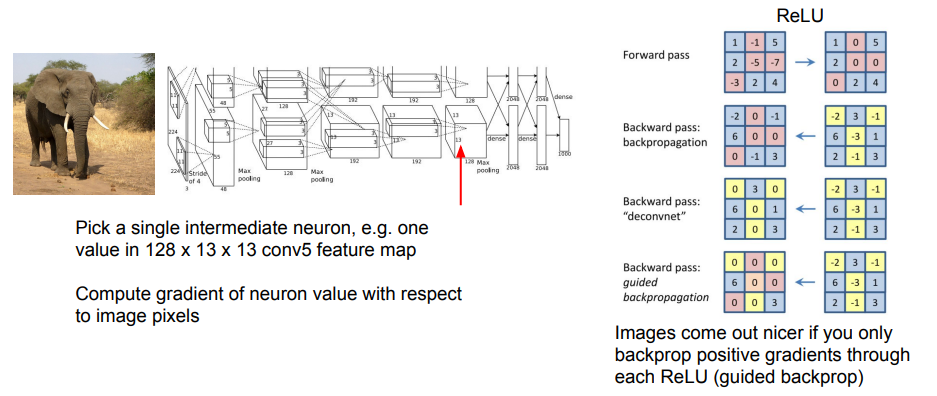
입력 이미지의 특정 부분이 최종 분류 점수 대신 중간 뉴런의 값에 주는 영향을 확인할 수도 있는데, 이때 'Guided Backpropagation'이라는 방법을 사용하면 조금 더 깨끗한 이미지를 얻을 수 있다.

간단하게, 역전파가 ReLU를 통과할 때 그래디언트의 부호가 양수면 그대로 통과시키고, 음수면 차단하여 전체 네트워크가 양수인 그래디언트만 고려하도록 만드는 원리이다.

• Guided Backpropagation의 결과를 살펴보면 일반적인 역전파를 사용했을 때에 비해 훨씬 더 뚜렷하게 형체가 나타나는 것을 볼 수 있음.
  

Gradient Ascent

지금까지처럼 어떤 고정된 입력 이미지에 대해 '뉴런의 활성화 여부'를 확인하는 대신, 거꾸로 해당 뉴런을 활성화시키는 '일반적인 입력 이미지'를 생성하고 싶을 때 사용하는 방법이다.

지금까지의 신경망의 목적과는 반대로, 네트워크의 가중치를 고정시킨 채로 특정 뉴런의 활성화 또는 최종 분류 점수가 최대화되도록 입력 이미지의 픽셀 값을 갱신해 나간다.

여기서도 Regularization 항이 사용되는데, (기존의 쓰임새와 비슷하게) 생성된 이미지가 특정 네트워크의 특성에 과적합되는 것을 막기 위함이다. 즉, 이미지가 특정 뉴런의 값을 최대화시키도록 생성되면서도 '자연스럽게' 보이도록 돕는다.

📌 과적합이 발생하면 계산 결과가 뉴런의 활성화를 최대로 만드는 이미지가 될 수는 있겠지만, 사람이 보기에는 '의미 없는 노이즈'처럼 보이게 된다.

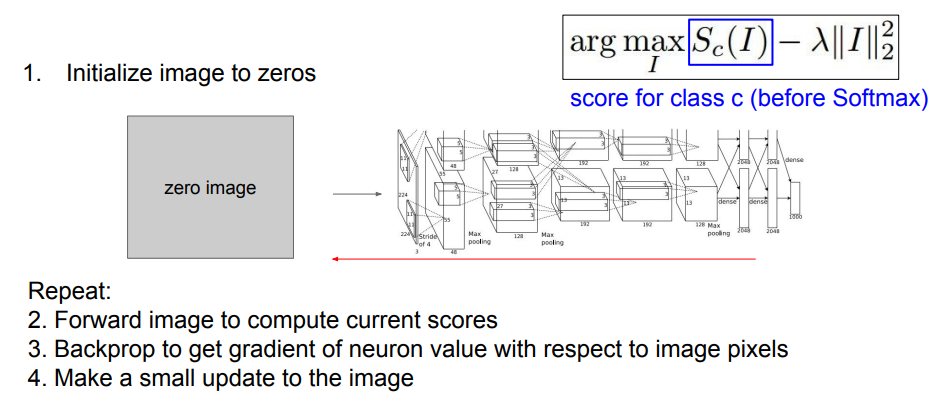
전체적인 과정은 이런 식으로 진행된다.

1. 입력 이미지를 초기화(가우시안 노이즈 등으로 설정)시킴.
2. 이미지를 네트워크에 통과시키고 관심 있는 뉴런의 점수를 계산함.
3. 이미지의 각 픽셀에 대한 해당 점수의 그래디언트를 계산하여 역전파를 수행함.
4. Gradient Ascent를 이용해서 입력 이미지의 픽셀을 조금 갱신함. 2~4를 반복하면 적합한 이미지가 완성됨!

• L2 Norm에 더하여 추가적인 최적화 방법을 적용하면 더 깔끔한 이미지를 얻을 수 있음. (주기적으로 이미지에 가우시안 블러 적용, 낮은 값 또는 기울기를 가진 픽셀을 0으로 설정 등등...)

DeepDream

입력 이미지를 CNN의 특정 레이어까지 순전파 시킨 후, 해당 레이어의 그래디언트를 자신의 Activation 값으로 설정하고, 역전파를 보내 이미지를 갱신하는 것을 반복하면 독특한 이미지를 생성할 수 있다. 이는 네트워크에 의해 검출된 이미지의 특징을 증폭시키는 것과 같다.

• 생성되는 이미지는 해당 CNN이 학습했던 데이터에 영향을 받음. 깊은 레이어를 대상으로 하면 실제 학습 데이터의 객체와 닮은 형상이 나타나고, 얕은 레이어를 대상으로 하면 엣지 등의 추상적인 형태가 관찰됨.

Feature Inversion

이미지를 네트워크에 통과시키고 나온 특징 맵으로부터 다시 이미지를 재구성함으로써, 이미지의 어떤 정보가 특징 벡터에서 포착되는지를 짐작할 수 있다.

여기서도 Gradient Ascent가 쓰이며, 점수를 최대화시키는 대신 주어진 특징 벡터와 새로 생성된 이미지의 특징 벡터 간 거리를 최소화시키는 방법을 이용한다. 이때 Total Variation Regularizer는 상하좌우 인접 픽셀 간 차이를 패널티로 부여한다.

각 계층별 결과를 보면 얕은 계층에서 나온 특징 맵일수록 원래의 이미지를 거의 정확하게 재구성하며, 깊은 계층의 특징 맵일수록 픽셀, 텍스처, 색깔 등의 정보를 잃어간다.

즉, 특징 네트워크가 깊어질수록 '정확한 픽셀 값'과 같은 저수준의 정보들은 사라지고, 대신 미세한 변화에 더 강인한 의미론적 정보들만이 남는다는 것을 유추할 수 있다.

Texture Synthesis

입력된 텍스처 패치와 비슷한 패턴을 가진 더 큰 패치를 생성하는 것으로, 다양한 방법을 통해 구현할 수 있다.

가장 고전적인 방법인 Nearest Neighbor는 주변 픽셀들 중 가장 가까운 픽셀을 계산하여 한 픽셀씩 이미지를 생성해 나가는 방식으로, 신경망이 쓰이지 않는 대신 복잡한 텍스처에는 적용하기 힘들다는 단점이 있다.

신경망을 통한 텍스처 합성(Neural Texture Synthesis)을 위해서는 'Gram Matrix'라는 개념이 필요하다. 이를 구하는 방법은 다음과 같다.

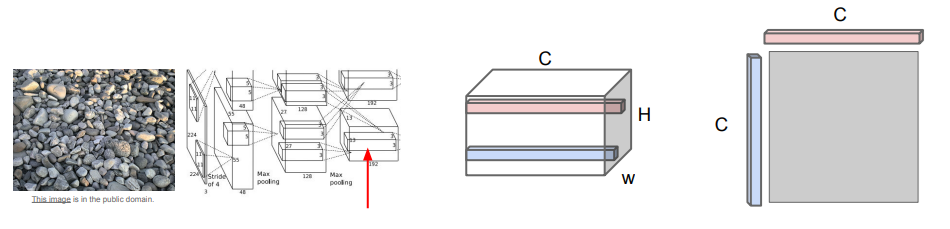
1. 이미지를 CNN에 통과시킨 후, 특정 레이어의 특징 맵(C×H×W)을 가져옴.
2. 특징 맵에서 서로 다른 두 개의 특징 벡터(C×1×1, C차원)를 뽑은 후, 외적(Outer Product)을 계산해서 2차원 행렬(C×C)로 만듦.
   • 위 행렬에는 '이미지 내 서로 다른 두 지점에 있는 특징들 간의 Co-Occurrence'가 담기게 됨. (서로 다른 공간에서 동시에 활성화되는 특징을 포착!)
3. 위 과정을 전체 특징 맵의 그리드(H×W)에서 전부 수행한 후, 결과에 대한 평균을 계산하면 C×C 크기의 Gram Matrix를 얻을 수 있음.

이렇게 얻은 Gram Matrix는 이미지의 각 지점에 해당하는 값들을 모두 평균화함으로써 공간 정보를 날려버리고 특징들 간의 Co-Occurrence만을 남기게 되며, 이를 입력 이미지의 텍스처를 기술하는 '텍스처 기술자'로 사용하여 이미지를 생성할 수 있다.

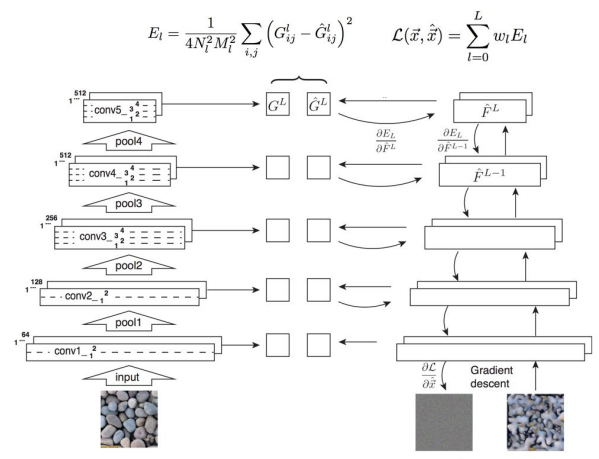
1. 사전 훈련된 모델(주로 VGG)을 다운로드하고, 입력 텍스처 이미지를 VGG에 통과시키면서 여러 레이어에서 Gram Matrix를 계산함.
2. 생성할 이미지를 초기화한 후, VGG에 통과시키면서 여러 레이어에서 Gram Matrix를 계산함. (Gradient Ascent와 유사)
3. 원본 이미지와 생성된 이미지의 Gram Matrix 간 차이를 L2 Norm을 통해 손실로 계산함.
4. 역전파를 통해 생성된 이미지의 픽셀의 그래디언트를 계산하고, Gradient Ascent를 통해 이미지의 픽셀을 조금씩 갱신함. 이를 반복하면 입력 텍스처와 유사한 이미지를 생성할 수 있음!

Style Transfer

위의 Texture Synthesis와 Feature Inversion을 조합하여 입력 이미지를 '특정 화풍'으로 변환할 수 있다.

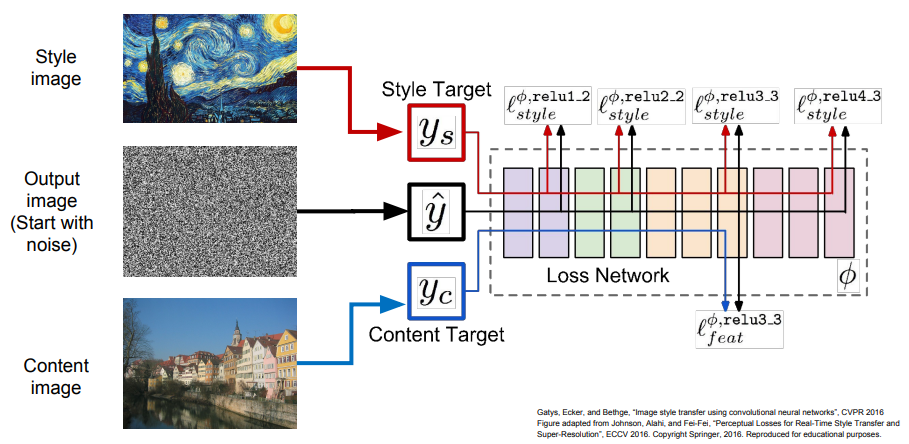
입력은 '최종 이미지의 형태'를 결정하는 Content Image와 '최종 이미지의 텍스처'를 결정하는 Style Image로 나뉘며, 이들을 네트워크에 통과시키고 각각 Gram Matrix와 Feature Map을 계산한다. 이후 순전파와 역전파를 반복하면서 Gradient Ascent를 이용해 출력 이미지를 갱신하면 된다.

• Style Loss와 Content Loss 간의 가중치를 조절하거나, Style Image의 사이즈를 조정하는 등 다양한 하이퍼파라미터의 조작이 가능함.
• 동시에 여러 Style Loss의 Gram Matrix를 계산하는 식으로 여러 화풍을 조합할 수도 있음.

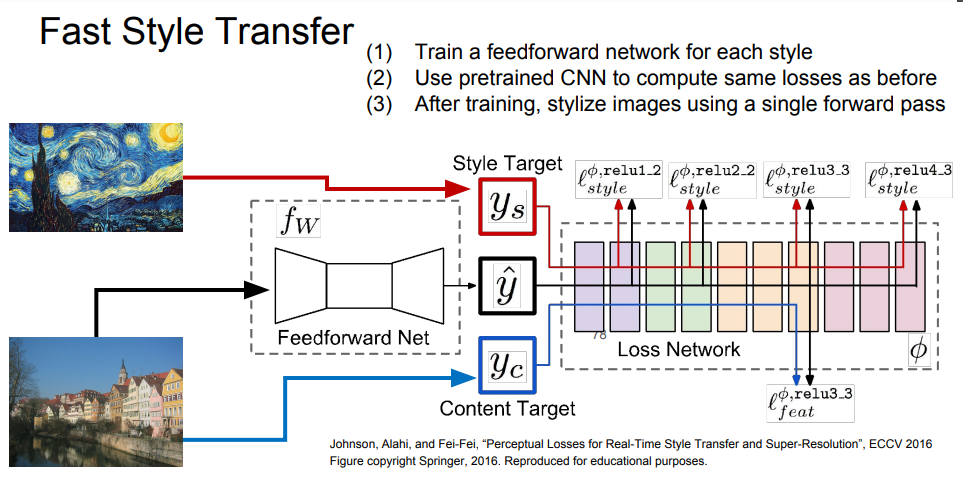
기존 Style Transfer의 단점은 아주 많은 순전파/역전파의 반복 수행이 필요하기 때문에 이미지 생성이 매우 느리다는 것이다.

반면, Fast Style Transfer는 Style Image는 고정시킨 채 Content Image만 입력으로 받아서 결과를 출력할 수 있는 단일 네트워크를 학습시키는 방법으로, 한 번 학습시키고 나면 입력 이미지에 대한 결과를 빠르게 얻을 수 있다.

13. Generative Models

Unsupervised Learning

지금까지의 지도 학습과 달리, 비지도 학습은 레이블 없이 오직 데이터 자체만 가지고 데이터에 숨어있는 기본적인 구조를 학습시키는 것이다. (ex. 군집화, 차원 축소, 특징 표현, 분포 추정 등)

Generative Models

생성 모델은 비지도 학습의 일종으로, 동일한 분포에서 새로운 샘플들을 생성해내는 모델이다. 이때 학습 데이터에 대한 분포 추정이 필요하다.

• 분포 추정은 생성 모델의 분포를 명시적으로 정의해 주는 방법(Explicit)과, 명시적으로 정의하지 않는 방법(Implicit)이 있으며, 어떤 분포 추정을 사용했느냐에 따라 생성 모델의 종류가 나뉜다.
  

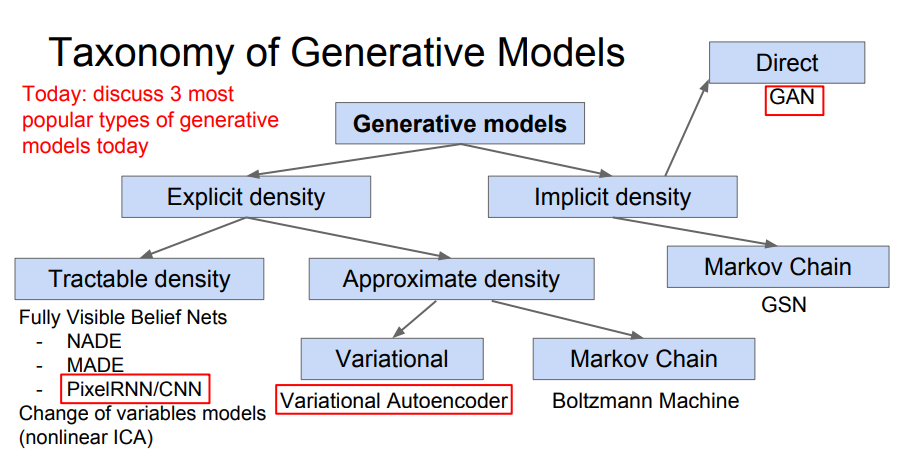
PixelRNN and PixelCNN

'Fully Visible Belief Network'의 일종으로, 밀도를 명시적으로 정의하고 모델링한다.

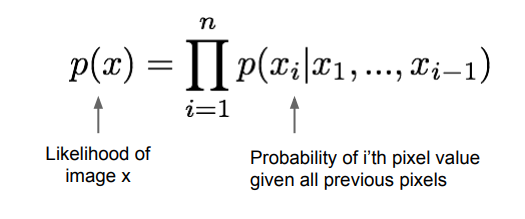
이미지 데이터 $x$에 대한 가능도(Likelihood) $p(x)$를 모델링할 때, 연쇄 법칙을 통해 가능도를 1차원 분포들 간의 곱의 형태로 분해한다. 그러면 각 분포는 이미지의 각 픽셀 $x_{i}$마다 모든 이전 픽셀들을 조건으로 갖는 분포가 된다.

가능도를 정의했으면 모델 학습을 위해 학습 데이터의 가능도를 최대화시키면 된다.

💡 가능도(Likelihood, 우도)란?

주어진 관측값이 어떠한 확률분포에서 나왔을 가능성을 의미한다. (참고 게시글)
'주어진 분포에서 어떠한 관측값이 나올 가능성'을 의미하는 Probability와 비슷하지만 반대의 개념이라 볼 수 있다.

이때 각 픽셀 값에 대한 분포는 '자기 이전의 모든 픽셀들'을 조건으로 가지므로 매우 복잡한데, 이러한 복잡한 변환은 신경망을 이용하면 잘 표현할 수 있다.

PixelRNN

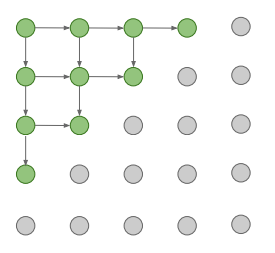
한쪽 모퉁이에서부터 화살표 방향의 연결성을 따라 각 픽셀을 순차적으로 생성하며, 이러한 방향성을 기반으로 한 픽셀들 간의 종속성을 RNN(LSTM)을 이용하여 모델링한다.

이 방법은 모든 픽셀이 생성될 때까지 순차적으로 네트워크를 수행시켜야 하므로 시간이 오래 걸린다는 단점이 있다.

PixelCNN

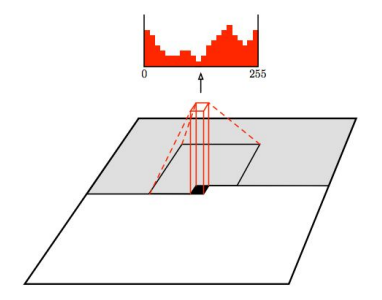
PixelRNN과 비슷한 방식이지만, 픽셀을 생성할 때 RNN 대신 CNN을 사용하여 특정 영역의 픽셀만을 고려하게 한다.

학습 이미지를 정답(레이블)으로 하여 생성된 이미지의 각 픽셀과 Softmax Loss를 계산할 수 있으며, 이는 [0, 255] 사이의 분류 문제를 푸는 것과 같다. 각 픽셀의 가능도를 최대화하도록 학습을 진행한다.

이때 사용되는 학습 이미지는 이미 알고 있는 값이므로 학습 과정을 병렬화시킬 수 있어 PixelRNN보다 더 빠르지만, 생성은 여전히 모퉁이에서부터 순차적으로 진행되므로 느리다.

• PixelRNN/CNN은 가능도 $p(x)$를 명시적으로 정의한 후 계산하는 방법이며, 따라서 'Evaluation Metric(평가 지표)'를 이용하여 생성된 샘플의 완성도를 평가할 수 있음.

Autoencoders (AE)

레이블이 없는 학습 데이터로부터 저차원의 특징 표현을 학습하기 위한 비지도 학습 방법이다.

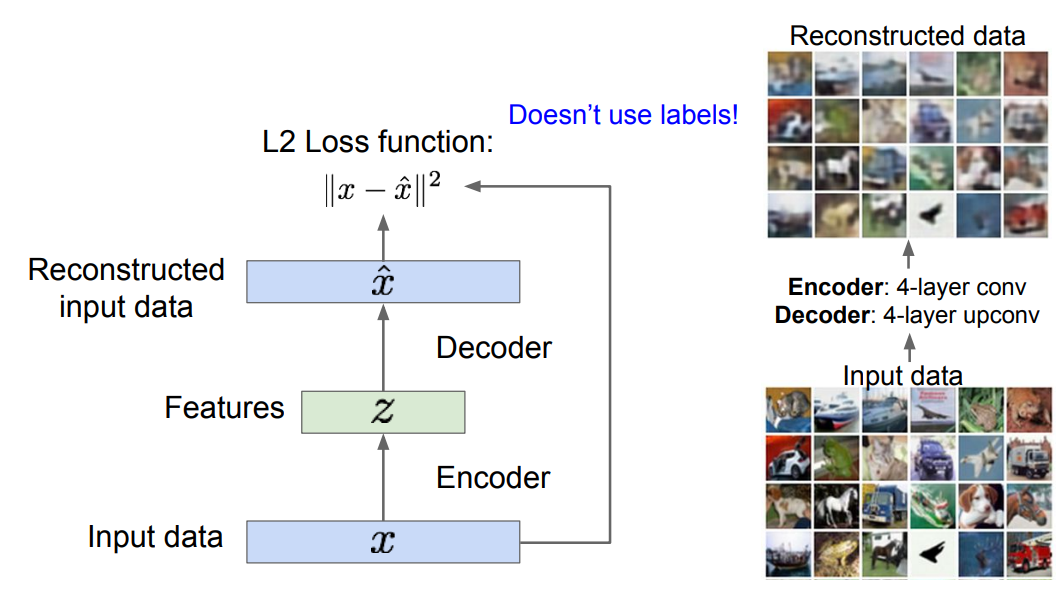
• Encoder: 입력 데이터 $x$를 (보다 낮은 차원의) 특징 $z$로 변환하는 매핑 함수의 역할을 하며, 다양한 종류의 신경망이 될 수 있음.
  • 왜 차원이 낮아져야 할까? ⇒ $z$가 데이터 $x$의 '가장 중요한 특징들'을 잘 담고 있어야 하므로!
• Decoder: 반대로 $z$를 입력으로 받아 원본 데이터 $x$와 동일한 차원이면서 유사한 데이터를 출력(복원)함. Encoder와 동일한 구조를 가짐.
  • CNN이 사용되었다면 일반적인 합성곱 대신 Upconvolution 연산이 사용됨.

AE는 복원된 이미지의 픽셀 값과 입력 이미지의 픽셀 값 간의 L2 Loss를 계산하여, 최종적으로는 두 값이 최대한 같아지도록 학습을 수행한다.

학습이 끝나면 Decoder는 버려지며, Encoder가 학습한 특징 매핑을 데이터가 부족한 지도 학습 모델의 초깃값으로 사용할 수 있다.

Variational Autoencoders(VAE)

AE에서 잠재(Latent) 변수인 벡터 $z$가 학습 데이터의 Variation을 잘 갖고 있으므로, 이를 새로운 데이터의 생성에 이용해 보자는 생각에서 출발한다.

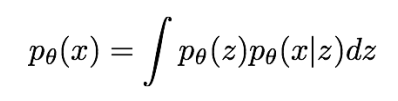
VAE에서는 먼저 적분을 이용하는 확률 모델을 정의한 후, 추가적인 잠재 변수 $z$를 모델링한다. 위 식은 직접 계산이 불가능하므로, 대신 $p_{θ}(x)$의 하한(Lower Bound)을 구해서 최적화해야 한다.

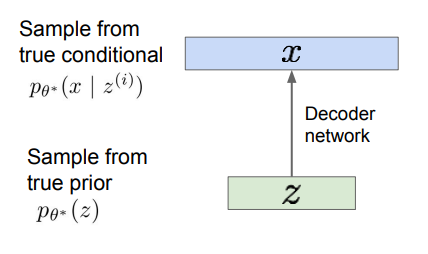
1. 먼저, 학습 데이터 $x_{i}$가 관측할 수 없는 잠재 변수 $z$에 의해 생성된다고 가정한다. 벡터 $z$의 각 요소들은 데이터의 다양한 요소들을 잘 포착하고 있을 것이다.
2. 생성 과정에서는 $z$에 대한 사전 분포(Prior Distribution) $p_{θ^*}(z)$를 택한 후 샘플링을 수행하여 $z$를 얻는다. (주로 가우시안 분포 선택)
3. 이후 조건부 분포(Conditional Distribution) $p_{θ^*}(x | z^{(i)})$를 통해 샘플링을 수행하여 $x$를 얻는다. (복잡한 분포이므로 신경망 사용)

결론적으로, 설계된 네트워크는 잠재 변수를 받아서 이미지로 디코딩하는 역할을 한다. (= Decoder Network)

생성 모델이 새로운 데이터를 잘 생성하게 하려면 True Parameter인 $θ^*$를 잘 추정해야 하므로 모델을 학습시켜야 한다.

가장 쉬운 방법은 모델 파라미터가 학습 데이터의 가능도 $p_{θ}(x)$를 최대화하도록 학습하는 것이지만, 데이터 가능도를 구하기 위한 적분식은 직접 계산할 수 없다(Intractability). 베이즈 정리를 통한 사후 분포 $p_{θ}(z|x)$를 대신 구하려 해봐도 여전히 $p_{θ}(x)$에 대한 적분이 매우 어렵다.

따라서 추가적인 Encoder Network $q_{Φ}(z|x)$를 정의하여 입력 $x$를 $z$로 인코딩하도록 한다. 이는 사후 분포 $p_{θ}(z|x)$를 근사시키는 역할을 하며, 데이터 가능도의 하한을 계산할 수 있게 된다.

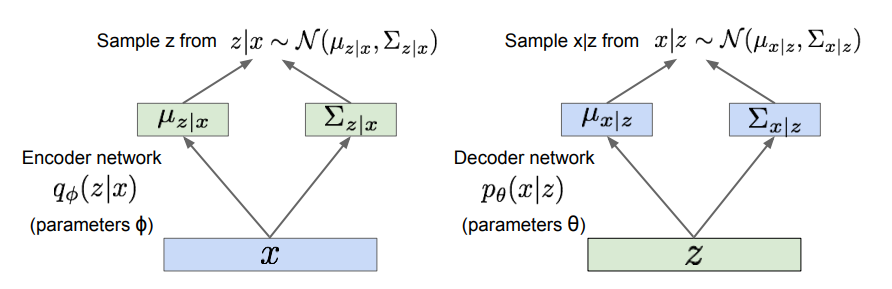
VAE도 AE와 같은 Encoder/Decoder 구조이며, 여기에 확률론적 의미가 추가된다.

• Encoder Network: 입력은 $x$이고, 출력은 $z|x$에 대한 평균과 (대각) 공분산이며, 파라미터 $Φ$를 가짐.
  • $z|x$라는 잠재 변수를 추론하는 역할을 하므로 Recognition(인식) 또는 Inference(추론) 네트워크라고 부르기도 함.
• Decoder Network: 입력은 $z$이고, 출력은 $x|z$에 대한 평균과 (대각) 공분산이며, 파라미터 $θ$를 가짐.
  • Generation(생성) 네트워크라고 부르기도 함.

이들의 분포로부터 샘플링하여 실제 $z|x$, $x|z$ 값을 얻을 수 있다. 다시 데이터 가능도 문제를 살펴보자.

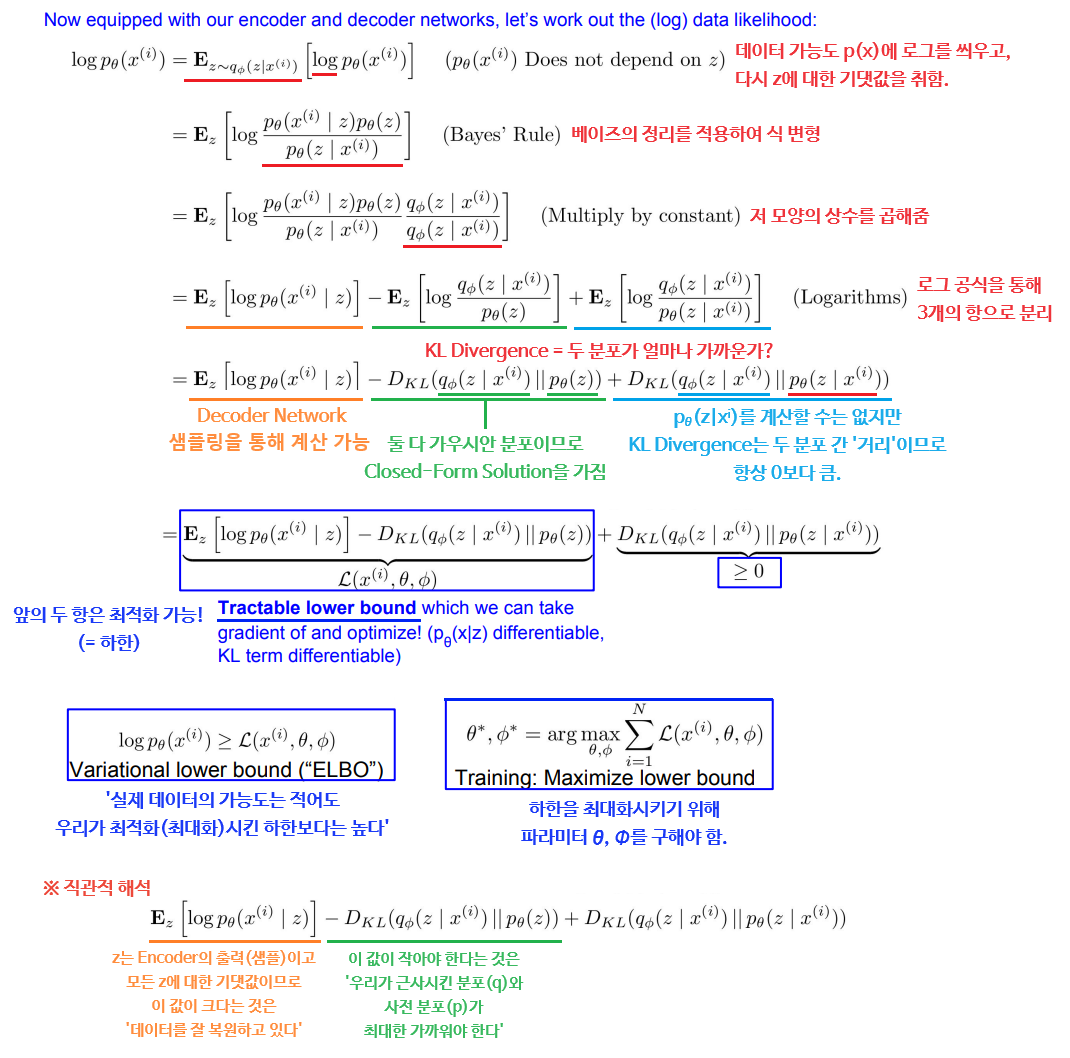
이제 Lower Bound를 구했으니 이를 통해 VAE를 학습시킬 수 있다. 학습 과정은 다음과 같다.

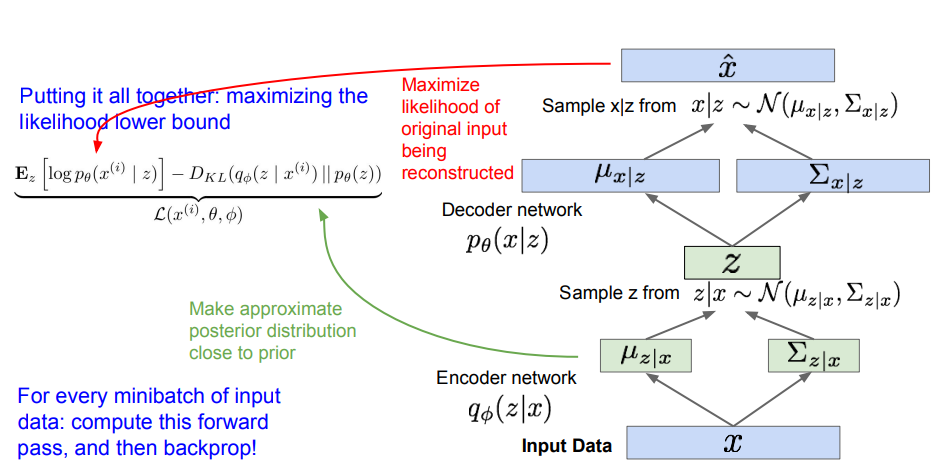
1. 순전파 단계에서 입력 데이터 $x$를 Encoder에 통과시켜 $q(z|x)$에 대한 평균과 분산을 얻는다.
2. $q(z|x)$는 KL Divergence를 계산할 때 이용할 수 있으며, 이 분포로부터 잠재 변수 $z$를 샘플링한다.
3. 샘플링한 $z$를 Decoder에 통과시켜 $p(x|z)$에 대한 평균과 분산을 얻는다.
4. 위 분포를 바탕으로 $\hat{x}$를 샘플링한다.
5. 복원된 이미지에 대한 가능도가 최대가 되도록 손실을 계산하고 파라미터 $Φ$, $θ$를 학습해 나간다.

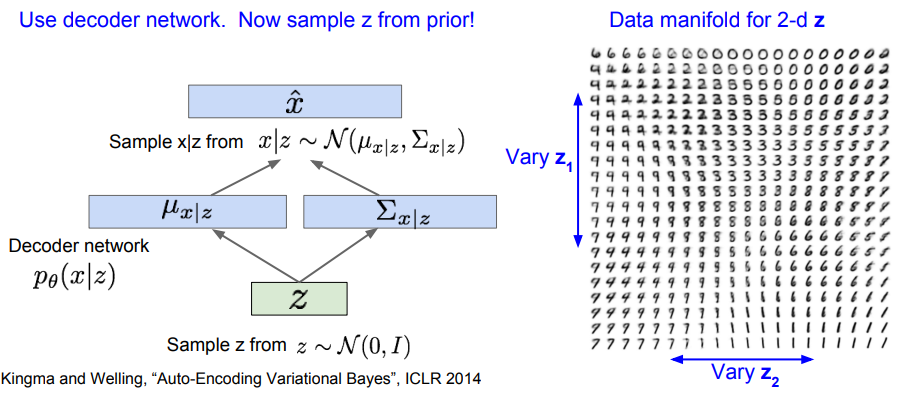
학습 이후 데이터 생성에는 Decoder만 필요하며, $z$를 사후 분포가 아닌 사전 분포(가우시안)에서 샘플링하고 이를 바탕으로 다시 데이터 $\hat{x}$를 샘플링한다.

이때 잠재 변수 $z$는 각 차원마다 독립적으로 해석 가능하고 다양한 의미론적인 요소들을 잘 인코딩하여 담고 있다. (미소의 정도, 머리의 각도 등)

• VAE는 AE의 '확률론적 변형 버전'이라 할 수 있음.
  • AE가 결정론적으로 $x$를 받아 $z$를 만들고 다시 $x$를 복원했다면, VAE는 데이터 생성을 위해 분포와 샘플링의 개념을 추가함.
• 계산할 수 없는(Intractable) 분포를 다루기 위해 근사시킨 하한(Lower Bound)를 계산함.
• GAN과 같은 현재 최고 수준(SOTA)의 생성 모델에 비해서 생성된 샘플이 흐려 보이고(Blur) 퀄리티가 낮은 경향이 있음.

Generative Adversarial Networks (GAN)

위의 모델들과 달리 확률 분포를 직접 모델링하지 않으며, 대신 '게임 이론'의 접근법을 사용한다.

복잡한 고차원 학습 분포에서 직접 샘플링을 수행하는 대신, 가우시안 노이즈 같은 더 단순한 분포에서 샘플링을 하고 우리가 원하는 학습 분포로 변환(Transformation)하는 함수를 학습하는 방법이다.

GAN에서는 입력으로 랜덤 노이즈 벡터 $z$를 받고, 생성 네트워크를 통과하면 학습 분포로부터 직접 샘플링된 값을 출력한다.

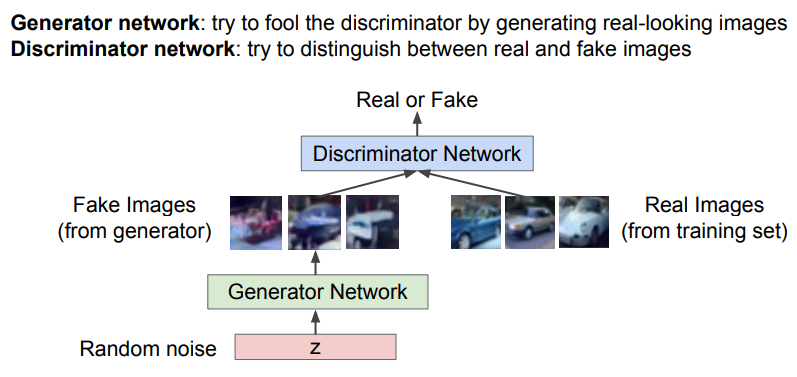
'Two-Player Game'이란, 생성자(Generator)와 판별자(Discriminator) 2개의 네트워크를 두고 '게임 플레이어'처럼 경쟁하게 하면서 학습을 진행시키는 방법론이다.

• 생성자: 사실적인 '가짜 이미지'를 생성하여 판별자를 속이는 것이 목표. 판별자를 더 잘 속이기 위해 점점 더 사실적인 이미지를 만들게 됨.
• 판별자: 입력된 이미지가 실제인지 거짓인지를 구별하는 것이 목표. 생성자의 가짜 이미지를 더 잘 구별하기 위해 점점 더 높은 판별력을 갖게 됨.

GAN의 Minimax Objective Function은 위와 같이 생겼다. 생성자의 파라미터인 $θ_{g}$는 위 값을 최소화시켜야 하고, 판별자의 파라미터인 $θ_{d}$는 반대로 최대화시켜야 한다. 이 균형을 맞추는 것이 매우 까다롭고 또 중요하다.

💡 Objective Function(목적 함수)란?

머신러닝에서 모델의 성능을 측정하는 척도로 쓰이는 함수이며, 모델의 목적에 맞게 최대화 또는 최소화하여 최적화하는 것이 목표이다. 손실 함수를 포함하는 개념이라 할 수 있다.

GAN을 학습시킬 때에는 두 네트워크를 번갈아가면서 학습시킨다. 판별자는 목적 함수의 값을 최대화시켜야 하므로 Gradient Ascent를, 생성자는 반대로 최소화시켜야 하므로 Gradient Descent를 이용해 보자. 생성자의 경우 자신의 파라미터인 $θ_{g}$가 있는 우측 항만 사용하면 된다.

하지만 실제로는 생성자의 학습이 잘 진행되지 않는데, 그 이유는 생성자의 성능이 좋을 때보다 나쁠 때일수록 그래디언트가 더 작아지기 때문이다. (즉, 많은 학습이 필요할 때 오히려 기울기가 더 작게 주어짐)

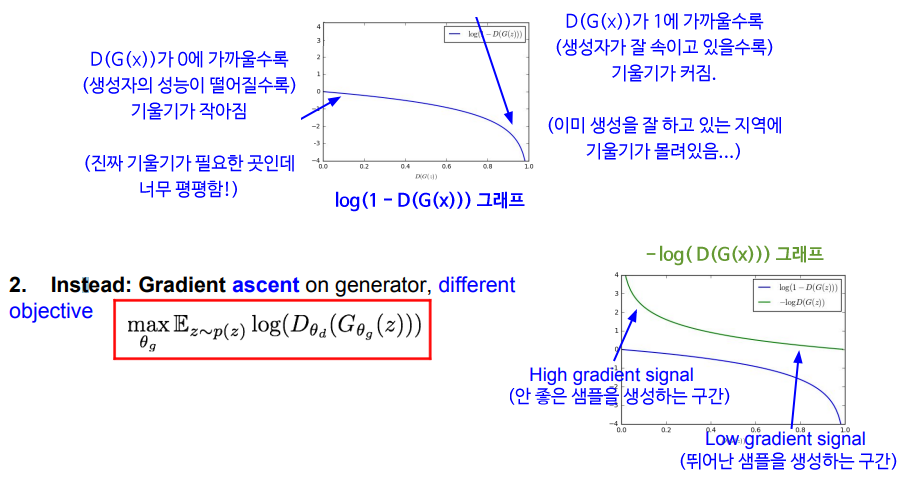
따라서 목적 함수를 살짝 변형하여 생성자도 Gradient Ascent를 사용하도록 한다. 판별자가 '맞출 가능도'를 최소화하는 대신, '틀릴 가능도'를 최대화하는 것이다.

• 실제 학습 시에는 판별자를 k번만큼 조금 학습시키고 그 다음 생성자를 학습시키는 방식을 사용함. 이때 안정적인 학습을 위한 k값 결정이 중요함.

• Deep Convolutional GAN(DCGAN):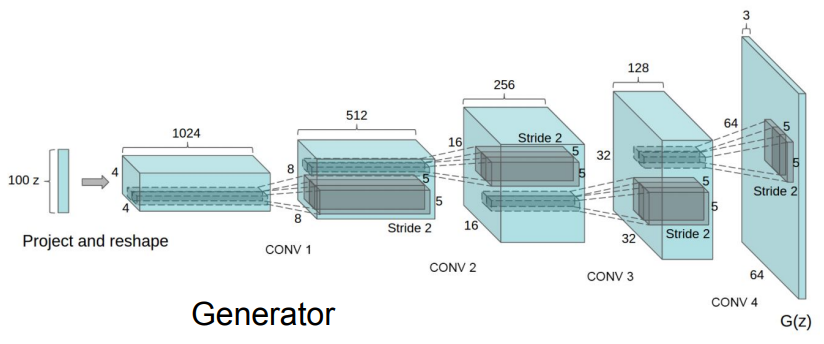기존 GAN의 성능을 높이기 위해 CNN 아키텍처를 추가한 버전. 입력 노이즈 벡터 $z$를 위와 같은 과정을 거쳐 샘플 출력으로 변환시킴.
  • 두 개의 랜덤 노이즈 $z$를 잡고 그 사이를 보간(Interpolation)하여 부드럽게 변하는 이미지를 만들 수도 있음.

• 벡터 $z$의 의미를 좀 더 이해하기 위해 서로 다른 특징을 가진 벡터 집합에서 각각 평균을 구한 후 더하고 빼본 결과이다.

14. Deep Reinforcement Learning

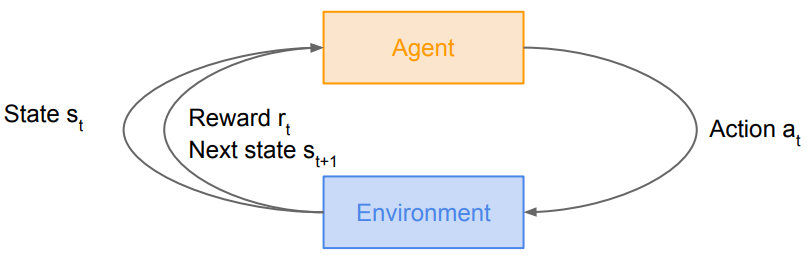
강화 학습(Reinforcement Learning)은 다음과 같이 요약된다.

에이전트(Agent)가 환경(Environment)에 대하여 어떠한 행동(Action)을 취하면, 그에 따라 환경의 상태(State)가 변하고 특정한 보상(Reward)을 받게 되며, 강화 학습은 에이전트의 보상을 최대화할 수 있는 행동이 무엇인지를 학습하는 것이다.

Markov Decision Process (MDP)

강화 학습 문제를 수식화하기 위한 방법이다. Markov Property를 만족하며, $(S, A, R, P, γ)$로 정의한다.

• Markov Property: 현재 상태만으로 전체 상태를 나타내는 성질.
• $S$ = 가능한 상태들의 집합
• $A$ = 가능한 행동들의 집합
• $R$ = (상태, 행동) 쌍이 주어졌을 때 받게 되는 보상의 분포 (매핑 함수)
• $P$ = (상태, 행동) 쌍이 주어졌을 때 전이될 다음 상태에 대한 분포 (전이 확률)
• $γ$ = 보상을 받는 시간에 대한 중요도 (Discount Factor)

또한, 다음과 같은 방식으로 동작한다.

1. 초기 타임 스텝은 0이고, 초기 상태는 초기 상태 분포로부터 샘플링함.
2. 에이전트가 행동을 선택함.
3. 환경은 어떤 분포로부터 보상과 다음 상태를 샘플링함.
4. 에이전트가 보상과 다음 상태를 받고, 2~4를 에피소드가 종료될 때까지 반복함.

💡 에피소드(episode)란?

강화 학습에서, 에이전트가 초기 상태부터 종결 상태에 도달하기까지 거친 일련의 과정을 의미한다. 가령, 게임을 강화 학습시킨다면 '게임 한 판'이 곧 하나의 에피소드가 됨.

MDP의 궁극적인 목적은 Cumulative Discounted Reward(누적 보상) $\sum_{t＞0}γ^{t}r_{t}$을 최대화시키는 최적의 정책 $π^*$를 찾는 것이다.

• 미래에 얻을 보상까지를 포함하는 개념이며, 이때의 보상은 'Discount Factor(할인율)'에 따라 할인되어 적용됨.

• 정책(Policy): 각 상태에서 에이전트가 '어떤 행동을 취할지'를 명시해 주는 기능을 함. 결정론적일 수도, 확률론적일 수도 있음.

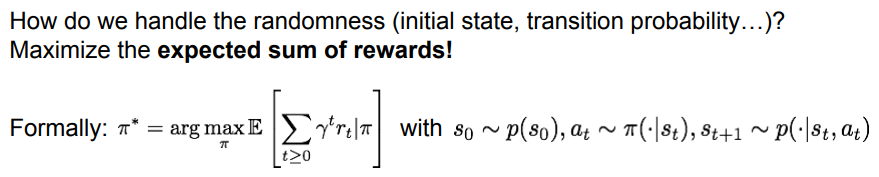
MDP에서 발생하는 무작위성(초기 상태 샘플링, 전이 확률 분포의 다음 상태 등)은 보상의 합에 대한 '기댓값'을 최대화시키는 방식으로 다룰 수 있다.

• 초기 상태는 '초기 상태 분포', 행동은 어떤 상태가 주어졌을 때 '정책이 갖는 분포', 다음 상태는 '전이 확률 분포'로부터 각각 샘플링됨.

Value Function and Q-Value Function

한 에피소드에서 정책에 따라 행동을 계속 취하다 보면, (상태, 행동, 보상)들로 이루어진 하나의 '경로'를 얻게 될 것이다. 각 상태가 '얼마나 좋은지'는 가치 함수를 통해서 알 수 있다.

• Value Function(가치 함수): 상태 $s$와 정책 $π$가 주어졌을 때의 누적 보상의 기댓값 (= '이 상태 자체가 얼마나 좋은가?')

• Q-Value Function(Q-가치 함수): 상태 $s$와 정책 $π$, 행동 $a$가 주어졌을 때의 누적 보상의 기댓값 (= '이 상태에서 이 행동을 취하는 것이 얼마나 좋은가?')

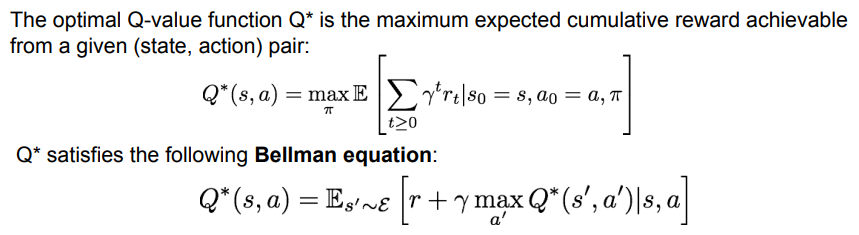
미래에 대한 보상을 최대로 만드는 '최적의 Q-가치 함수'인 $Q^*$가 있다고 가정하면, 이는 (상태, 행동) 쌍으로부터 얻을 수 있는 누적 보상의 기댓값을 최대화시키면서 벨만 방정식을 만족할 것이다.

• 벨만 방정식: 임의의 $(s,a)$ 쌍에 대하여, $Q^*$은 현재 $(s,a)$ 쌍을 통해 받을 수 있는 보상 $r$과 에피소드가 종료될 $s'$까지의 보상을 더한 값의 기댓값과 같음.
  • 일종의 점화식으로, 현재 상태의 가치 함수와 다음 상태의 가치 함수 간 관계를 나타냄.
• 우리가 이미 '최적의 정책'을 알고 있다고 가정했기 때문에, 미래의 보상을 최대화하는 현재 스텝에서의 최적 행동을 택할 수 있음.

Deep Q-Learning

위에서 가정했던 실제 '최적의 정책'을 구하기 위한 방법으로 Value Iteration 알고리즘을 사용해 볼 수 있다. 이는 벨만 방정식을 통해 매 스텝마다 반복적으로 $Q_{i}$를 조금씩 최적화해나가는 방법으로, $i$가 무한으로 갈수록 점차 $Q^*$에 수렴하게 된다.

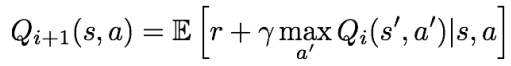
위 방법의 단점은 반복적인 업데이트를 위해 모든 (상태, 행동) 쌍에 대하여 $Q(s,a)$를 계산해야 한다는 것이다. (= 'Not Scalable')

가령, 비디오 게임을 강화 학습시키는 경우 스크린에 보이는 모든 픽셀이 각각 상태가 되므로 엄청나게 큰 상태 공간이 존재하게 된다.

이를 해결하기 위해, 함수 $Q^{*}(s,a)$를 $Q(s,a;θ)$라는 함수로 심층 신경망을 이용해 근사시켜 보자. $θ$는 함수의 파라미터이자 신경망의 가중치이다. 이 함수 역시 Q-함수이므로 벨만 방정식을 만족해야 하고, 따라서 신경망 학습을 통해 벨만 방정식과의 에러가 최소가 되도록 학습시키면 된다.

손실 함수는 $Q(s,a;θ_{i})$가 목적 함수(= 벨만 방정식) $y_{i}$와 얼마나 멀리 떨어져 있는지를 측정한다. 순전파에서는 손실을 계산하고, 역전파에서는 계산한 손실을 기반으로 파라미터 $θ$를 업데이트한다.

Q-Network Architecture

실제 '아타리 게임'에 강화 학습을 적용한 예시를 살펴보자. 게임의 목적은 최대한 높은 점수를 획득하는 것이며, 상태는 게임의 화면을 이루는 전체 픽셀, 행동은 상하좌우 조작 등이 있고, 매 시간 단위마다 점수에 따른 보상을 얻는다.

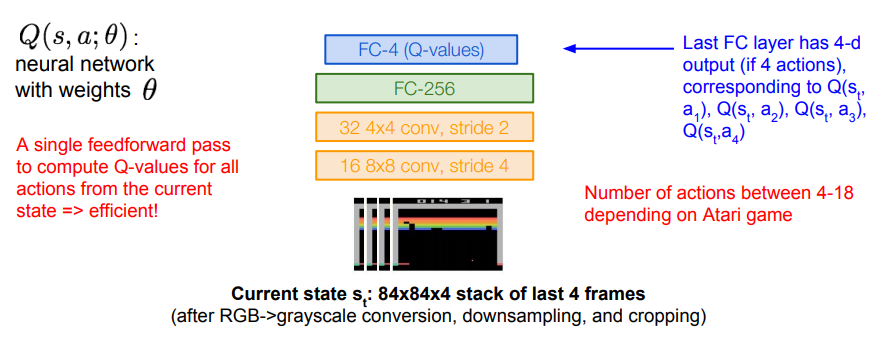
Q-함수에 사용한 네트워크의 입력은 스크린(4프레임 누적)의 픽셀이며 곧 '상태'의 역할을 한다. 이미지 전처리와 합성곱 계층, 완전연결 계층을 거쳐 주어진 상태에 대한 각 '행동'들의 Q-Value 값을 출력한다. 단 한 번의 순전파만으로 현재 상태에서의 모든 행동에 대한 Q-Value를 얻을 수 있다는 것이 장점이다.

Experience Replay

Q-Network를 학습시킬 때, 만약 하나의 배치에서 시간적으로 연속적인 샘플들로 학습을 수행한다면 모든 샘플들이 서로 상관관계를 가지므로(Correlated) 비효율적이고, 'Bad Feedback Loop'를 일으킬 수 있다.

Experience Replay는 이러한 문제를 해결하기 위해 (상태, 행동, 보상, 다음 상태)로 구성된 전이 테이블을 갖는 'Replay Memory'를 이용하며, 게임을 진행하며 더 많은 경험을 얻음에 따라 전이 테이블을 지속적으로 업데이트시킨다.

💡 전이(Transition)란?

강화 학습에서, 하나의 상태가 새로운(다음) 상태로 바뀌는 것을 말한다. 위처럼 'State' 뿐 아니라 행동, 보상과 같은 개념도 포함할 수 있다.

그리고 이 Replay Memory에서 임의로 미니배치를 샘플링하여 Q-Network를 학습시킨다. 연속적인 샘플들을 사용하지 않으므로 상관관계 문제로부터 자유롭고, 전이 테이블에서 하나의 샘플이 여러 번 뽑힐 수 있게 되므로 데이터 효율도 증가하게 된다.

• 한 에피소드의 각 타임 스텝마다 전이 테이블을 갱신하고 미니배치를 샘플링하여 학습시킨다.
• 실제 학습 시에는 항상 정책에 따른 최적의 행동만을 택하는 대신, 작은 확률로 '임의의 행동'을 취하게 하여 더욱 다양한 상태 공간을 샘플링할 수 있게 함.

Policy Gradients

Q-Learning의 단점은 함수가 매우 복잡하다는 것으로, 매우 큰 고차원 공간에서 가능한 모든 (상태, 행동)의 쌍들을 학습시키는 것은 매우 어려운 문제다.

반면, '정책' 자체는 이에 비해 훨씬 더 간단할 수도 있다. 그렇다면 이러한 정책 자체를 학습시킬 수는 없을까?

가중치 $θ$를 통해 매개변수화된 정책 집합을 $Π$라고 하고, 각 정책마다 '미래에 받을 보상들의 누적 합의 기댓값'인 $J(θ)$를 갖는다면, 이 값을 최대로 만드는 최적의 정책 $θ^*$를 찾기 위한 방법으로 정책 파라미터에 대해 Gradient Ascent를 수행할 수 있다.

REINFORCE Algorithm

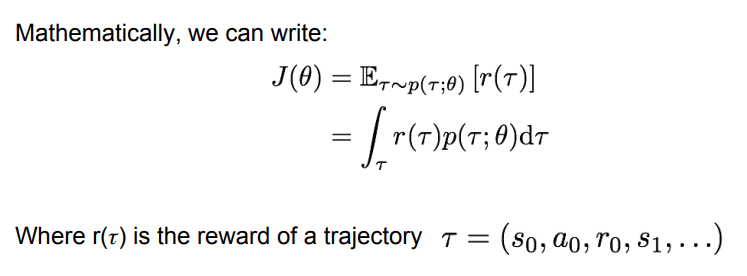
수학적으로 $J(θ)$는 '경로에 대한 미래 보상의 기댓값'으로 나타낼 수 있으며, 이를 위해 게임 플레이 시의 에피소드로부터 경로 $τ$를 샘플링할 수 있다. 경로는 어떤 정책 $π_{θ}$을 따라 결정되었을 것이고, 따라서 각 경로를 따라갔을 때의 보상 $r(τ)$을 계산할 수 있다.

그럼 Gradient Ascent를 위해 $J(θ)$의 그래디언트를 구해보자. 아래 그림과 같은 과정을 거치면, 경로에 대한 확률 $p(τ;θ)$의 그래디언트를 통해 $J(θ)$의 그래디언트를 구할 수 있음을 알게 된다.

그렇다면 전이 확률을 모르는 채로 $p(τ;θ)$을 구할 수 있을까? 역시 아래 그림의 과정에 따르면, 전이 확률 없이도 $p(τ;θ)$의 그래디언트를 구할 수 있다는 사실을 확인할 수 있다. 즉, 어떤 경로에 대해서도 그래디언트를 기반으로 $J(θ)$을 추정해 낼 수 있다.

정리하면, 어떤 경로로부터 얻은 보상이 클수록(즉, 어떤 일련의 행동들이 잘 수행한 것이라면) 그 일련의 행동들을 할 확률을 높여주고, 보상이 낮다면 해당 확률을 낮춰주면 된다.

• 단순히 경로의 보상이 크다고 경로에 포함된 모든 행동을 '좋은 행동'으로 취급해도 되는 이유는, 기댓값을 통한 Average-Out 덕분이다.

하지만 아직 여기에는 분산이 높다는 문제가 존재한다. 구체적으로 '어떤 행동이 최선이었는지'라는 정보까지 Average-Out 되기 때문이다.

Variance Reduction

Policy Gradients에서 분산을 줄이는 것은 더 적은 샘플링으로도 Estimator의 성능을 높일 수 있는 방법이므로 매우 중요하다. 이를 위한 3가지 아이디어가 있다.

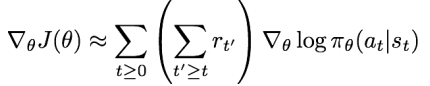1. 해당 상태로부터 받을 '미래'의 보상만을 고려하여 어떤 행동을 취할 확률을 높여준다. (즉, 맨 처음부터가 아닌 현재의 타임 스텝에서부터 종료 시점까지의 보상의 합만 고려)

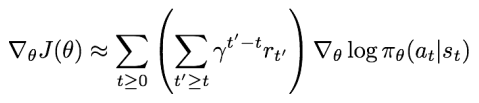2. 지연된 보상에 대한 할인율을 적용하여, '당장 받을 수 있는 보상'과 '조금 더 늦게 받는 보상' 간의 차이를 구별시킨다. (즉, 행동의 좋고 나쁨을 평가할 때 가까운 것을 위주로 고려)

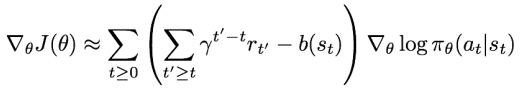3. Baseline: 어떤 행동을 취해 얻은 보상이 '얻을 거라 예상했던 보상(= Baseline)'보다 더 좋은지 아닌지를 판단한다.
   • Baseline은 보통 지금까지 경험했던 보상들에 대한 이동 평균(Moving Average)을 사용함.

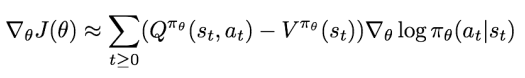
이때 세 번째 방법에서 더 좋은 Baseline을 택하는 방법으로, 위에서 나온 Q-Learning의 '가치 함수'를 이용하여 (Q-가치 함숫값) - (가치 함숫값)이 최대가 되도록 할 수도 있다. (어떤 행동을 취했을 때와 안 취했을 때의 미래 보상 누적값 비교)

Actor-Critic Algorithm

그렇다면 REINFORCE 알고리즘 상에서 Q-함수와 가치 함수를 구할 수 있는 방법이 있을까? ⇒ Policy Gradient와 Q-Learning을 조합하여 Q-함수와 가치 함수를 학습시키면 된다!

여기서는 Actor가 '정책'의 역할(어떤 행동을 취할지 결정)을, Critic이 'Q-함수'의 역할(해당 행동이 얼마나 좋았는지 알림)을 한다. 기존 Q-Learning처럼 모든 (상태, 행동) 쌍을 학습하는 대신, 정책이 만들어낸 쌍에 대해서만 학습을 시키면 된다.

수도 코드로 나타내면 아래와 같다.

마지막으로, Policy Gradients를 활용한 예시를 살펴보자.

• Recurrent Attention Model(RAM): 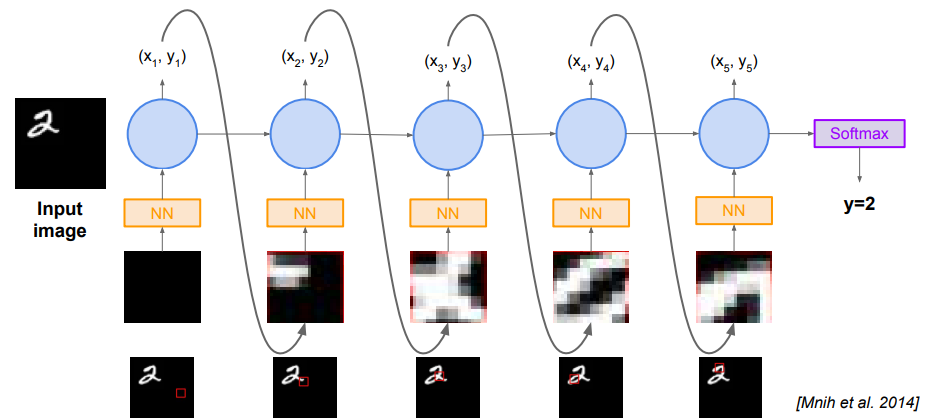이미지를 분류하기 위해 '어떤 부분을 살펴볼 것인지(Glimpse)'를 결정하는 데에 REINFORCE 알고리즘을 사용한다.
  • Hard Attention: 이미지의 전체가 아닌 일부분만 '집중하여' 살펴보는 식으로 분류를 추측하는 기법. 계산 자원을 절약할 수 있으며, '필요 없는 부분'을 무시할 수 있으므로 성능도 좋아짐.

• AlphaGo: 프로 바둑 기사의 기보를 통해 기사가 두는 수들을 지도 학습으로 학습하고, Policy/Value Network를 통해 현재 바둑판의 상태에서 어떤 수를 두어야 하는지를 결정함.

---

정리

강의 후반부에서는 CNN 및 RNN 아키텍처, 컴퓨터 비전 관련 문제들, 생성형 모델, 강화 학습과 같은 조금 더 심도있고 다양한 주제에 대해 배울 수 있었다.

정말 다양한 모델들과 방법론이 소개되었지만 더 깊은 이해를 위해서는 실제 논문을 하나씩 읽어 보면서 집중적으로 학습해야 할 필요성을 느꼈다. (ResNet, LSTM, VAE 등등...) 프로그래밍 스킬을 늘려서 간단한 모델의 경우 실제 코드로 구현해 보는 것도 이해에 큰 도움이 될 것 같다. 또, 내용이 심화될수록 내게 선형대수학이나 통계학 관련 지식이 꽤 많이 부족하다는 것을 느꼈다. 이 부분도 추가적인 공부를 통해 보완해 나가야겠다.