[백준] 2623번: 음악프로그램

1. 문제 이해

여러 원소들 중 일부 원소들의 순서만이 부분적으로 주어졌을 때, 이 순서들을 위배하지 않으면서 전체 순서를 알맞게 결정하는 문제이다.

예를 들어, 순서 1 → 2 → 3과 4 → 2 → 5가 주어졌을 때, 전체 원소는 1 → 4 → 2 → 3 → 5와 같은 방식으로 정렬할 수 있다. (서로 명확한 순서 관계가 주어지지 않은 원소들끼리는 어떻게 배치되어도 괜찮다)

다행히 얼마 전 이와 비슷한 유형의 문제를 위상 정렬을 통해 해결할 수 있다는 것을 배웠다.

2. '위상 정렬'이란?

위상 정렬은 비순환 방향 그래프(Directed Acyclic Graph, DAG)의 정점들을 각 간선들의 방향을 거스르지 않도록 나열하는 것을 의미한다.

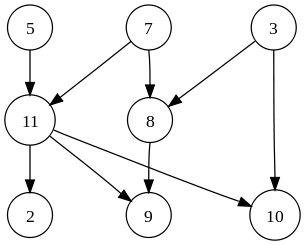
위와 같은 그래프가 있을 때, 11 → 5 또는 9 → 8처럼 간선의 방향을 거스르는 부분이 없도록 전체 순서를 결정하는 방법은 이렇다.

1. 각 정점마다 진입 차수와 진출 차수를 구한다.
2. 그중에서 진입 차수가 0인(즉, 어떤 정점으로부터도 도달하지 않는) 정점 v를 선택하고 출력한다.
3. v와 연결된 진출 간선을 제거한다. 모든 v → w에 대해 w의 상응하는 진입 간선도 제거한다.
4. 이제 일부 정점의 진입 차수에 변동이 생겼을 것이다. 2번으로 돌아가 과정을 반복한다.
5. 만약 모든 정점을 출력하기 전에 진입 차수가 0인 정점을 찾을 수 없다면 그래프에 순환이 존재하는 것이고, 이때는 전체 순서를 결정할 수 없다.

이 방법은 이번 문제에 정확히 적용할 수 있다.

단, 코드에서는 시간 복잡도를 줄이기 위해 매번 모든 정점의 모든 진출 정점들의 개수를 세는 대신, 진출 차수를 정점별로 in_counter 배열에 저장하여 사용하는데, 이때 중복된 경로가 주어질 경우 카운트하지 않는 것에 유의하자.

3. 코드

import sys

input = sys.stdin.readline

N, M = map(int, input().split())
in_node = [[False] * (N + 1) for _ in range(N + 1)]  # 노드별 진입 노드
out_node = [[False] * (N + 1) for _ in range(N + 1)]  # 노드별 진출 노드
in_counter = [0] * (N + 1)  # 노드별 진입 차수
res = []

for _ in range(M):
    arr = list(map(int, input().split()))[1:]
    for i in range(1, len(arr)):  # arr[i - 1] -> arr[i]
        if not in_node[arr[i]][arr[i - 1]]:
            in_counter[arr[i]] += 1  # 중복된 경로가 아닐 때에만 카운트
        in_node[arr[i]][arr[i - 1]] = True
        out_node[arr[i - 1]][arr[i]] = True

for i in range(N):  # 총 N번 반복
    v = None
    for j in range(1, N + 1):
        if in_counter[j] == 0:  # 진출 차수가 0인(= 최상단의) 노드를 선택
            v = j
            in_counter[j] -= 1  # 중복 방문하지 않도록 -1로 설정
            break

    if not v:  # 사이클이 있는 경우 진출 차수가 0인 노드가 존재하지 않게 됨
        break
    res.append(v)

    for k in range(1, N + 1):  # 해당 노드와 연결된 모든 진출 간선을 제거
        if out_node[v][k]:
            out_node[v][k] = False
            in_node[k][v] = False  # 상대 노드의 상응하는 진입 간선도 제거
            in_counter[k] -= 1


if len(res) < N:
    print(0)
else:
    for r in res:
        print(r)