Git Diff / Android DiffUtil Deep Dive - 1

Android Recyclerview Adapter 에서 리스트 간 갱신에 사용되는 DiffUtil 에서는 클래스 내부에 정의된 calculateDiff 함수 를 이용해 new, old list 의 diff 를 찾아내고, Git 에서는 diff 라는 명령어를 이용해 파일 간 내용을 비교하여 선택적으로 변경사항을 저장하고 기존 작업 복사본과 병합할 수 있는 기능을 가지고 있다.

이 둘은 내부적으로 동일한 알고리즘(Myers' diff Algorithm 논문) 을 사용한다. 이 게시물에서는 diff 알고리즘이 어떻게 동작하는지에 대해 논문 내 그래프 기반으로 정리를 해보고자 한다.
(예시는 Git diff 로 설명하고자 한다.)

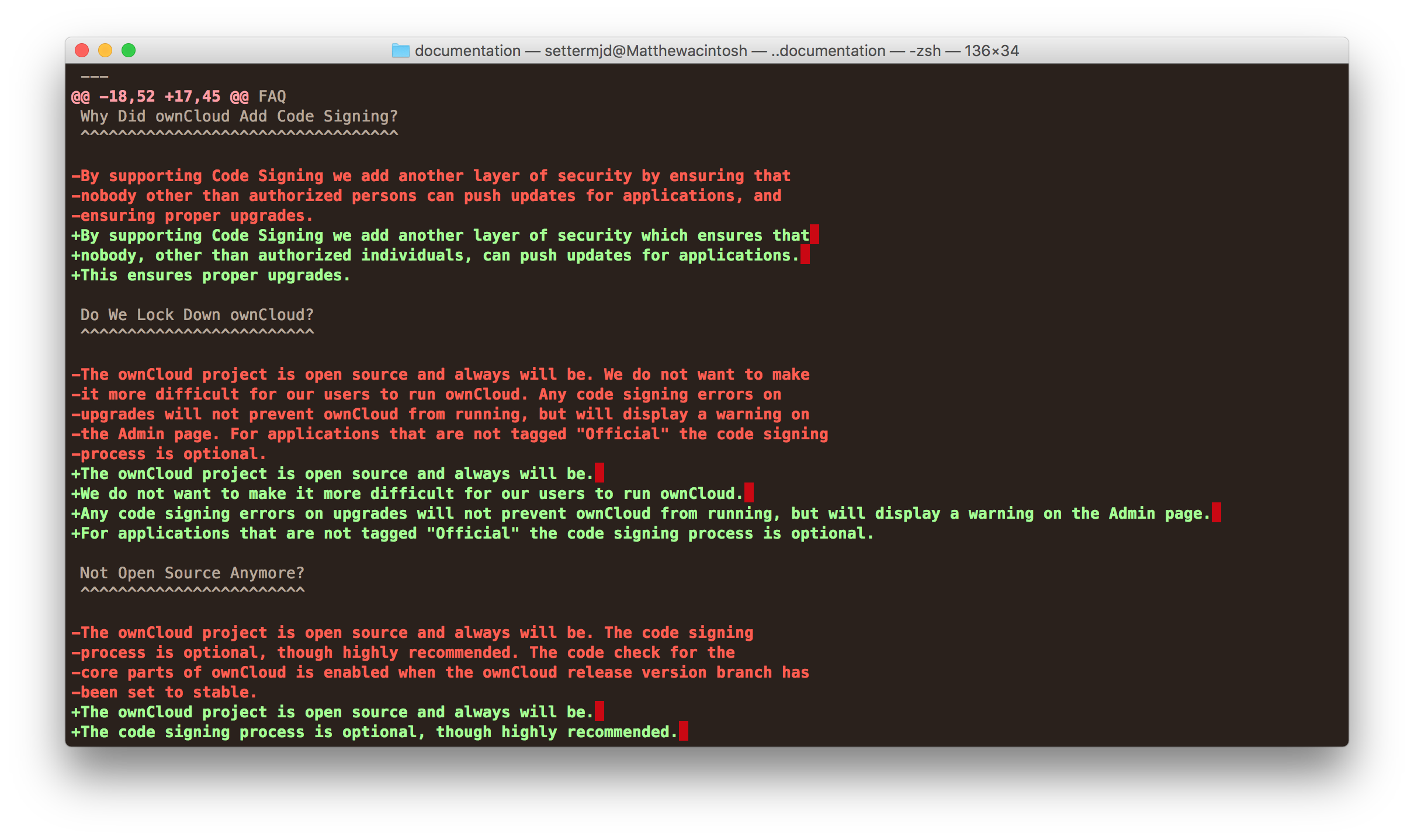
terminal 로 git diff 를 확인해보면 변경되지 않은 사항은 그대로 유지되고, 제거된 라인과 추가된 라인은 구분하여 쉽게 볼 수 있다. 그렇다면 파일내의 특정 라인이 변경되고, 삭제되고, 유지되었는지 어떻게 판단할 수 있을까?

예시를 활용해보도록 하겠다. 아래 A, B 문자열 간 변경점(diff) 를 계산하고 싶다고 가정해보자.

A = ABCABBA
B = CBABAC

여기서 변경점(diff) 이란, 문자열 A 를 B 로 변환하는 편집 과정을 의미한다. 변환하는 많은 방법 중 한가지는 A 문자열을 모두 삭제한 뒤, B 문자열을 삽입하는 방식이다.

하지만 우리가 원하는 것은 위와 같이 삭제와 추가를 일괄적으로 모두 보여주는 것이 아닌, 삽입 / 삭제 / 유지되는 문자열 이 공존하는 diff 를 보고싶을 것이다.

    1234567 <- 아래 문자의 인덱스라고 가정해보자
A = ABCABBA
B = CBABAC

앞서 문자열 A, B 가 다음과 같을 때 A 에서 B 로 변경하는 diff 는 아래와 같은 순서로 진행된다.

1. A1 삭제
2. A2 삭제
3. C3, B1 이 같으므로 유지 (C)
4. B2 추가
5. B3, A4 가 같으므로 유지 (A)
6. B4, A5 가 같으므로 유지 (B)
7. A6 삭제
8. B5, A7 이 같으므로 유지 (A)
9. B6 추가

사실 두 문자열의 diff 가 유일하게 이 방법만 있는 것은 아니다. 아래와 같이 다른 방법도 많이 존재할 것이다. (단, 가능한 가장 적은 비용으로 편집이 가능한 경우의 수만 고려한다.)

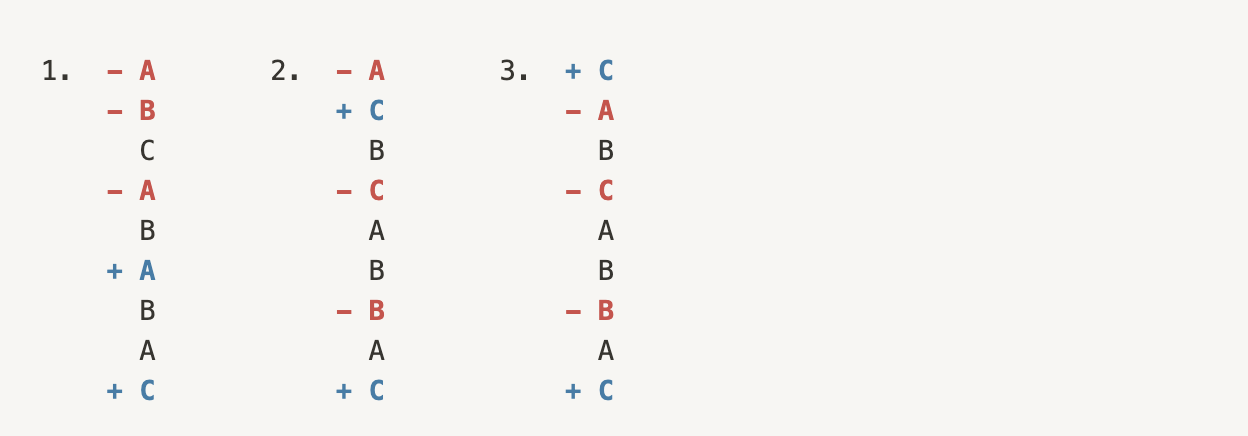
이 경우의 수들은 결과는 같지만, 삽입과 제거의 순서가 다르다는 것이다. 여기서 알아야 할 것은, diff 알고리즘의 전략은 삭제 후 삽입을 보여준다는 것이다. 즉 삽입보다 삭제의 우선순위가 더 높다는 의미이다.

이 전략을 바탕으로 다시 경우의 수를 보았을 때, 3번의 케이스가 다른 케이스들에 비해 좋지않은 삽입, 삭제 순서를 가지고 있음을 알 수 있다.

삽입보다 삭제의 우선순위가 더 높은 이유는 맨 처음 첨부된 terminal git diff 사진에서도 유추할 수 있다.
우리가 무엇인가를 변경하고자 할 때 삭제 후 삽입이 바로 이어지면서, 서로 얽혀있는 것보다 전체적으로 삭제된 lines 뒤에 새로운 lines 가 삽입되는 모습이 우리가 볼 때 더 익숙하기 때문이다.

그래서, Myers diff 알고리즘은 이러한 전략 중 하나이며, 보다 양질의 diff 를 제공한다. 변화가 생기기 전에 같은 행의 수를 최대한 많이 소비하려고 노력하며, 선택사항이 주어졌을 때 삽입보다 삭제를 선호함으로써 삭제가 먼저 나타나도록 한다.

Myers diff 논문을 바탕으로 A = ABCABBA, B = CBABAC 문자열에 대해서 A -> B 에 대한 diff 얻는 과정을 그래프로 표현해보고자 한다.

(x, y) 좌표로 이루어진 2차원 표와 그에 상응하는 문자열을 배치한 모습이다.

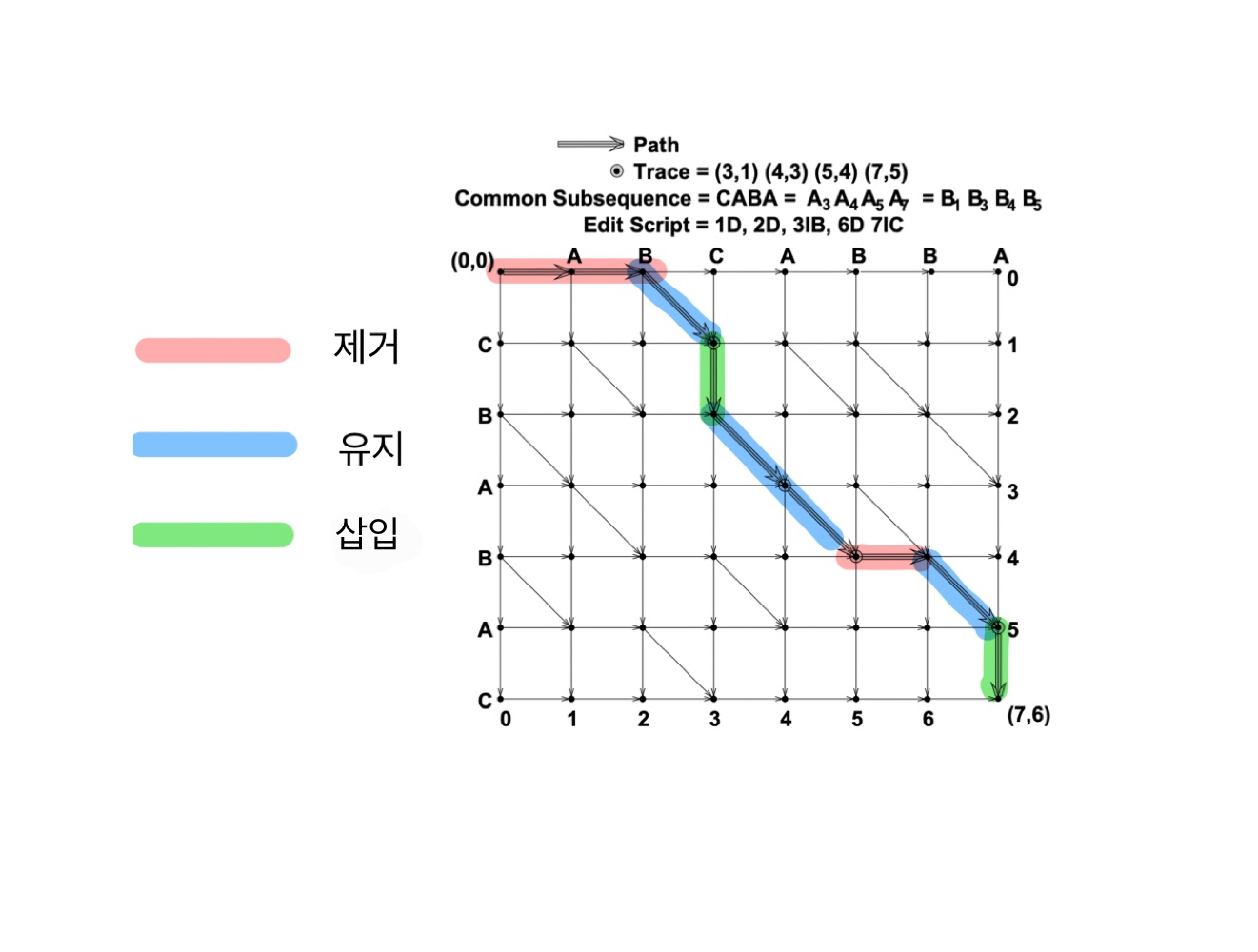
세로축이 B(CBABAC) 이고, 가로축이 A(ABCABBA) 이다.

좌표가 오른쪽으로 이동하는 경우는 A 에서 문자를 삭제한다는 의미이고, 아래로 이동하는 경우는 B 에서 문자를 삽입한다는 의미이다. 위 그래프에 그려진 방향을 예시로 들어보자면, (0,0) 에서 (2,0) 으로 이동하면서 A 문자열의 A, B 가 제거된다는 의미이고 (3, 1) 에서 (3,2) 로 내려감으로써 B 문자열의 B 가 추가된다는 의미이다.

오른쪽, 아래로 이동하는 것 외에도 대각선으로 이동이 가능하다. 대각선으로 이동하는 것은 두 문자열의 위치 인덱스에 동일한 문자가 있다는 것을 의미한다. 예시로, A 문자열의 첫번째로 등장하는 C 와 B 문자열의 C 가 동일하므로 삽입 및 삭제가 일어나지 않기에 이 때는 대각선으로 이동하는 것이다. 그래프로 보자면 (2,0) 에서 (3,1) 로 이동할 때라고 볼 수 있다.

Myers diff 알고리즘의 아이디어는 매우 간단하다. 가능한한 적은 수의 이동으로 맨 하단(7,6) 으로 이동하는 경우의 수를 찾는 것이다.

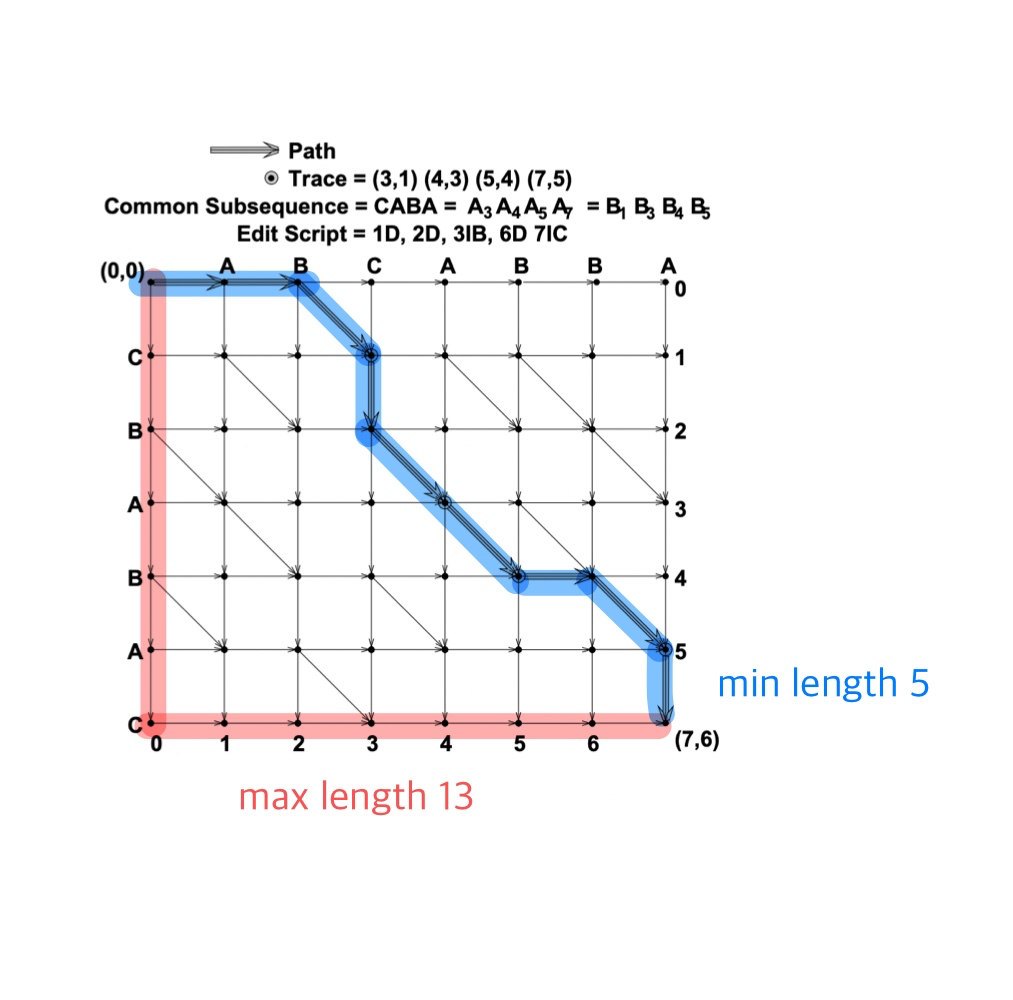
오른쪽 혹은 아래로 이동하는 것이 한 단계에 해당되며 우리가 맨 하단으로 이동하기 까지 취할 수 있는 가장 많은 수의 이동은 13이고, (A 의 길이 + B 의 길이) 가장 적은 수로의 이동은 5이다. (대각선은 변경에 해당하지 않으므로 비용이 들지 않는다, 즉 오른쪽 이동 횟수 + 아래 이동횟수 로 판단할 수 있다.)

이것이 바로 Android Diff Util 에 관한 설명을 찾아볼 때 종종 이야기하는 시간 복잡도, 공간 복잡도와 연결된다. (논문 초록에서도 등장한다.)

일반적으로 블로그에서 diff Util 을 설명할 때 아래와 같이 설명한다.

변경점을 찾는 비용
공간복잡도 : O(N)
시간복잡도 : O(N + D^2)

M의 추가항목과 N의 제거항목을 찾게 될 O(MN)의 추가 시간복잡도

이 때 말하는 N 은 비교하고자 하는 A, B 의 diff 중 그래프의 맨 하단으로 이동하고자 하는 "최대 이동 거리(위에서는 13을 뜻함)", D 는 "최소 이동거리(위에서는 5를 뜻함)" 를 나타낸다는 것을 볼 수 있다.
이 구성으로 BigO 가 결정되는 것이다.