Mask.
어떤 비트를 남겨두고, 지울지 결정을 지을 용도로 걸러내는 것. 이라고 보자
masking이라 함은 이러한 mask를 value에다가 적용하는 것을 뜻한다.
Bit-Masking
AND를 masking
1 1 1 0 1 1 0 1 [input] (&) 0 0 1 1 1 1 0 0 [mask] ------------------------------ 0 0 1 0 1 1 0 0 [output]
XOR를 masking
1 1 1 0 1 1 0 1 [input] (^) 0 0 1 1 1 1 0 0 [mask] ------------------------------ 1 1 0 1 0 0 0 1 [output]
장점
- 수행시간이 빠르다.
O(1)로 구현되는 것이 많다. - 코드가 간결하다.
- 메모리 사용량이 적다.
연산자
A / B 가 존재한다고 하자.
-
AND 연산
A = 1, B = 1일 때
C = A & B -> C = 1 -
OR 연산
A = 1, B = 0 혹은 A = 0, B = 1
둘 중 하나라도 1인 경우
C = A | B -> C = 1 -
XOR 연산
A = 1, B = 0 혹은 A = 0, B = 1
둘 중 하나만 1인 경우
C = A ^ B -> C = 1 -
NOT 연산
A = 1 일 때 C = ~A -> 0
A = 0 일 때 C = ~A -> 1 -
시프트(shift) 연산
정수 A의 비트들을 왼쪽 또는 오른쪽으로 원하는 만큼 움직인다.
움직이고 나서 빈자리는 0으로 채워지게 된다.
ex) 13 (1101)을 오른쪽으로 1bit 움직인다고 하면, 6 (0110)이 되는 것이다.
(ex. c = (a << 1) )
주의 할 점
첫 번째 C에서 비트 연산자들의 우선순위는 비교 연산자보다 낮다. 따라서 원하는 답이 나오지 않을 가능성이 있다.
예를 들어서 c = (6 & 4 == 4) 라고 한다면, 4 == 4가 먼저 계산되어 1(true)을 반환하고, 따라서 c에는 6 & 1의 값이 할당되게 된다.
따라서 비트 연산자를 이용할 때에는 항상 연산자마다 괄호를 씌워주는 것이 바람직하다.
두 번째로는, 오버플로우(Overflow) 문제이다.
2^50을 구하기 위해서 1<<50 으로 표현한다면, C에서는 1은 32bit 상수 취급하기 때문에 50번 왼쪽으로 shift하게 되면 overflow가 발생하게 된다. 따라서 1LL로 표현을 해주어야 한다.
subset의 합(BOJ 1208 부분수열의 합2)
사실 비트마스크를 한번 읽어보려 한 이유는 BOJ 1208 부분수열의 합2 문제 때문이다.
지금 해놓은 풀이는 dfs를 이용해서 모든 부분집합의 합을 구하는 방법인데, 비트마스크를 이용해서 모든 부분집합의 합을 구한 다음에 그 개수를 곱해주는 방식도 있다고 해서 찾아본 것이다.
일단 이 문제는 입력을 받는 경우의 수가 매우 커서 이 수열을 반틈 갈라서 왼쪽, 오른쪽으로 나뉜 두 집합에 대한 부분집합의 합을 구하려 하는 것이다.
그렇다면 이럴 땐 3가지 경우가 존재한다.
- 왼쪽의 부분집합으로 target을 성립 시킬수 있다.
- 오른쪽의 부분집합으로 target을 성립 시킬수 있다.
- 왼쪽, 오른쪽 부분집합이 합쳐져서 target을 성립 시킬수 있다.
그래서 공집합이 존재한다.
일단 왼쪽부분의 집합의 합만 구해 보았다.
import sys
n,s = map(int, sys.stdin.readline().split())
a = list(map(int, sys.stdin.readline().split()))중간을 나눠주면서 분할을 해준다.
우리는 이중 for문을 이용해서 부분집합의 합을 구할 것이다.
일단 n번 인덱스를 포함해서 부분집합을 구한다.
# 이분 분할
m = n//2
n = n - mn번 인덱스를 포함하는 부분집합의 모든 경우를 0으로 초기화 해 둔다.
현재의 경우 n = 3
가지고 있을 수 있는 인덱스의 경우는. [인덱스를 1, 2, 4] 로 보자.
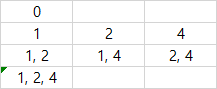
8가지 경우 위의 인덱스 값을 모두 더한 다면
0 ~ 7 까지 (1 << 3) 까지의 값이 된다.
# first : 왼쪽 Subset
first = [0] * (1<<n)이 때에 필요한 것이.
i -> 몇 번째 인덱스를 포함하고 있는 부분집합인지를 나타냄.
k -> 현재 대응해볼 인덱스를 나타냄.
num을 이용해서 현재 인덱스를 2진수? 로 만든다. 대응을 할 수 있도록.
# 비트마스킹을 이용하여 Subset의 합을 담는다
for i in range(1 << n):
for k in range(n):
num = 1 << k
pivot = i & num
if pivot > 0:
first[i] += a[k]
print(first)이렇게 부분집합을 만들어 놓은 후의 경우는 두 item 들을 더해서
target 보다 클 때, target보다 작을 때, 같을 때를 처리해준다.
같을 때의 경우에 현재 item이 계속 반복해서 나오는지에 대한 예외처리가 필요하다.
참고:
https://stackoverflow.com/questions/10493411/what-is-bit-masking
https://rebro.kr/63
https://peisea0830.tistory.com/40
