
이전 글과 이어집니다. 이진 트리의 연결 리스트를 통한 구현에 대한 내용입니다.
이전 글 보러가기
이진 트리 탐색
이진 트리를 탐색하기 위해 재귀적 방법을 사용하고자 합니다. 먼저 탐색 종류를 설명을 해보자면..
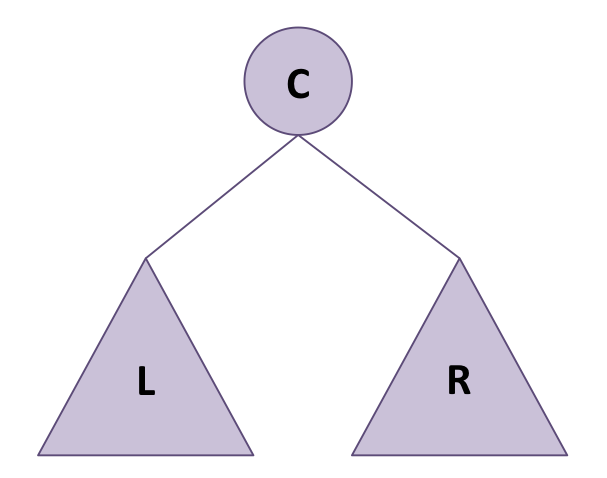 일단 이 그림을 머리에 넣고 다음 글을 보시길 바랍니다.
일단 이 그림을 머리에 넣고 다음 글을 보시길 바랍니다. C는 Root인데 Right와 혼동을 방지하기 위해 Center로 적었습니다.
재귀식 탐색을 하기 때문에 노드가 아닌 서브트리로 작성한 것입니다!
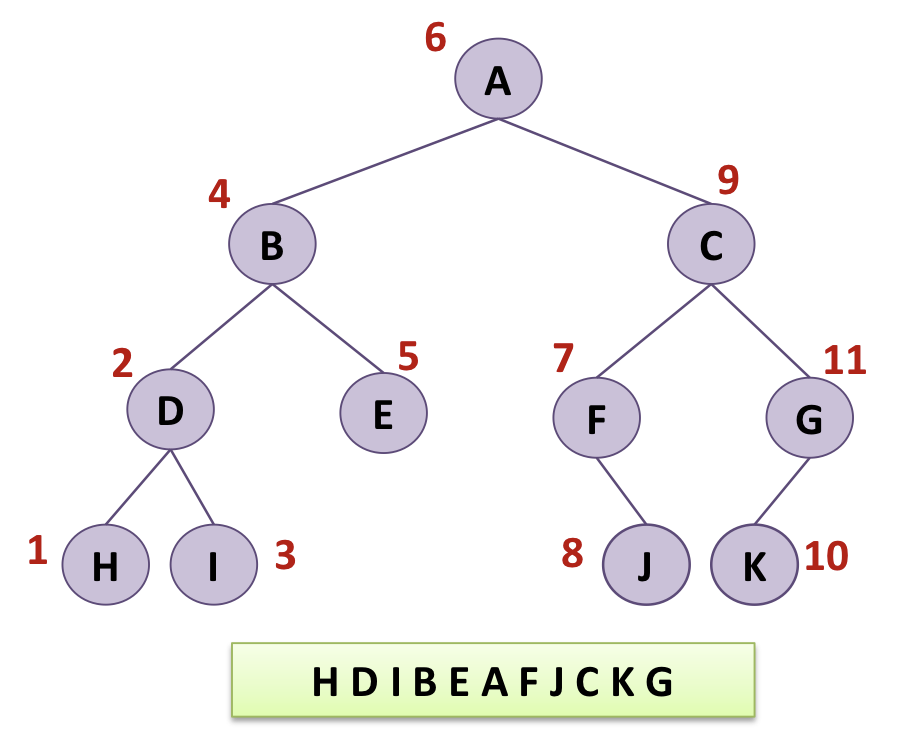
Inorder Traversal - LCR
- 왼쪽 서브트리 -> 루트 노드 -> 오른쪽 서브트리
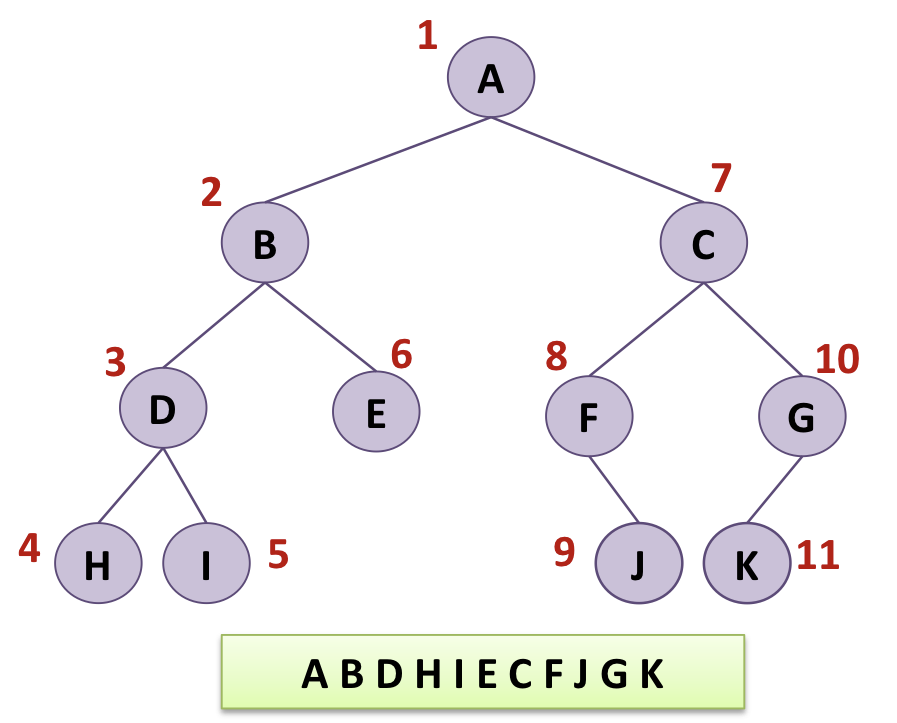
Preorder Traversal - CLR
- 루트 노드 -> 왼쪽 서브트리 -> 오른쪽 서브트리
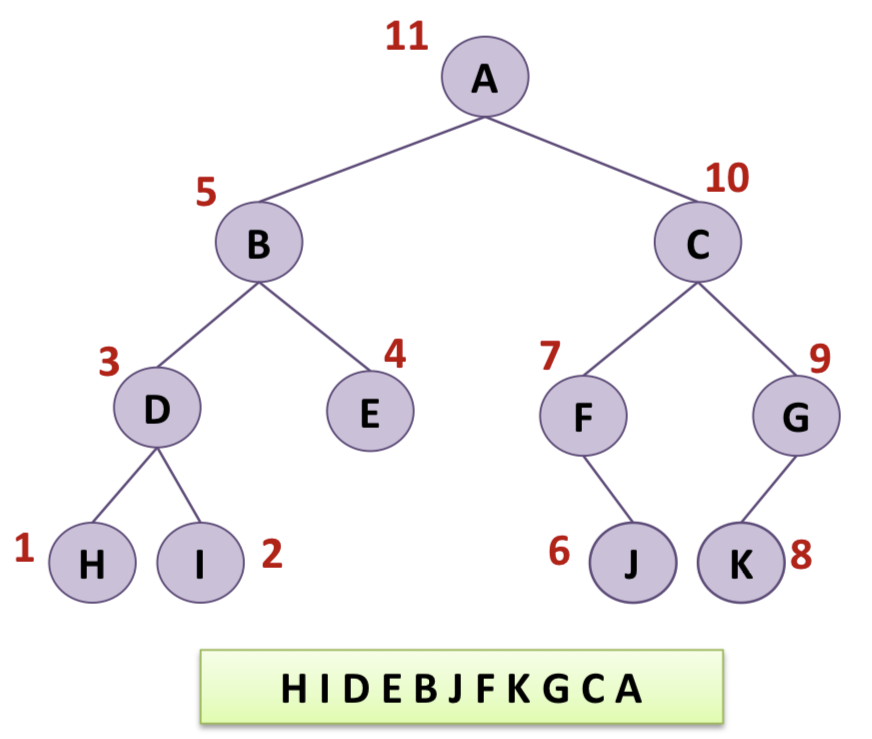
Postorder Traversal - LRC
- 왼쪽 서브트리 -> 오른쪽 서브트리 -> 루트 노드
Level Order Traversal
- 레벨 순서에 따라 노드 탐색
이 정도로만 적고 바로 구현으로 들어가 보겠습니다.
구현
Inorder Traversal - LCR
void Inorder(BTreeNode* root) {
if (root != NULL) {
Inorder(root->left_child); // L
cout << root->item; // C
Inorder(root->right_child); // R
}
}모든 과정이 재귀적 구조에 의해 진행됩니다.
Preorder Traversal - CLR
void Preorder(BTreeNode* root) {
if (root != NULL) {
cout << root->item << " "; // C
Preorder(root->left_child); // L
Preorder(root->right_child); // R
}
}Postorder Traversal - LRC
void Postorder(BTreeNode* root) {
if (root != NULL) {
Postorder(root->left_child); // L
Postorder(root->right_child); // R
cout << root->item << " "; // C
}
}Level Order Traversal
지금까지 탐색을 재귀적 방법으로 했다면, 레벨 순서에 따른 탐색은 큐(Queue)를 이용합니다.
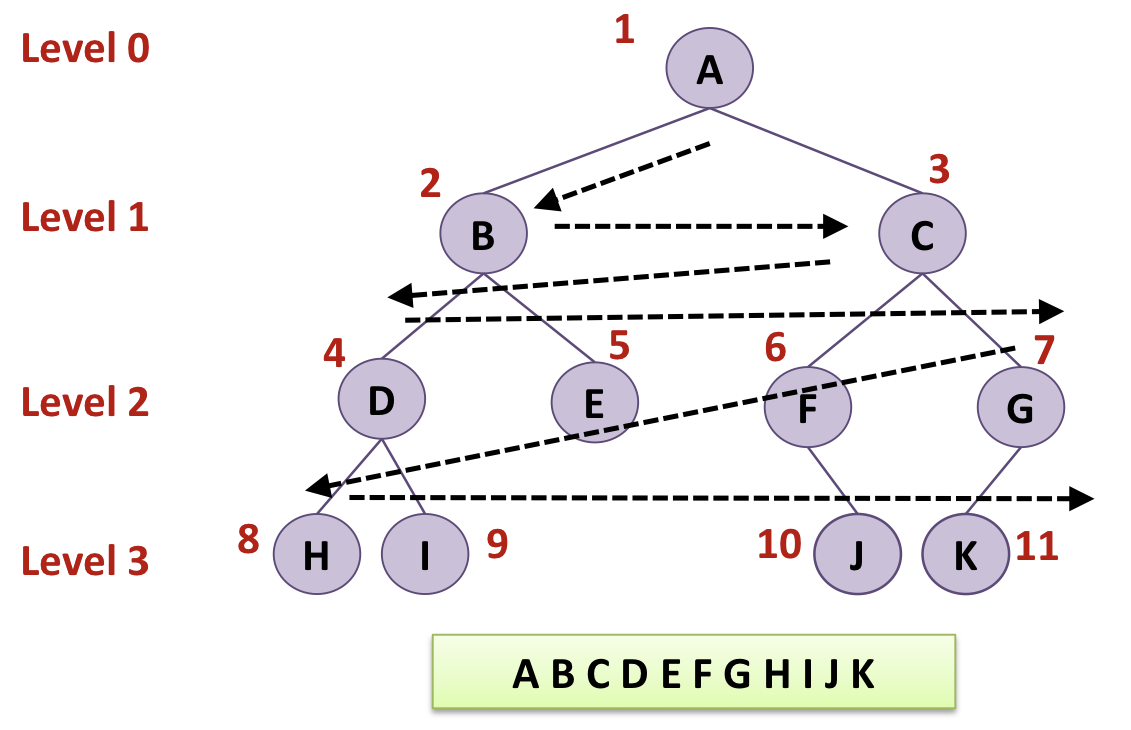 그림과 같이 이 순서대로 탐색하는 방식입니다.
그림과 같이 이 순서대로 탐색하는 방식입니다.
큐를 적용해보자면..
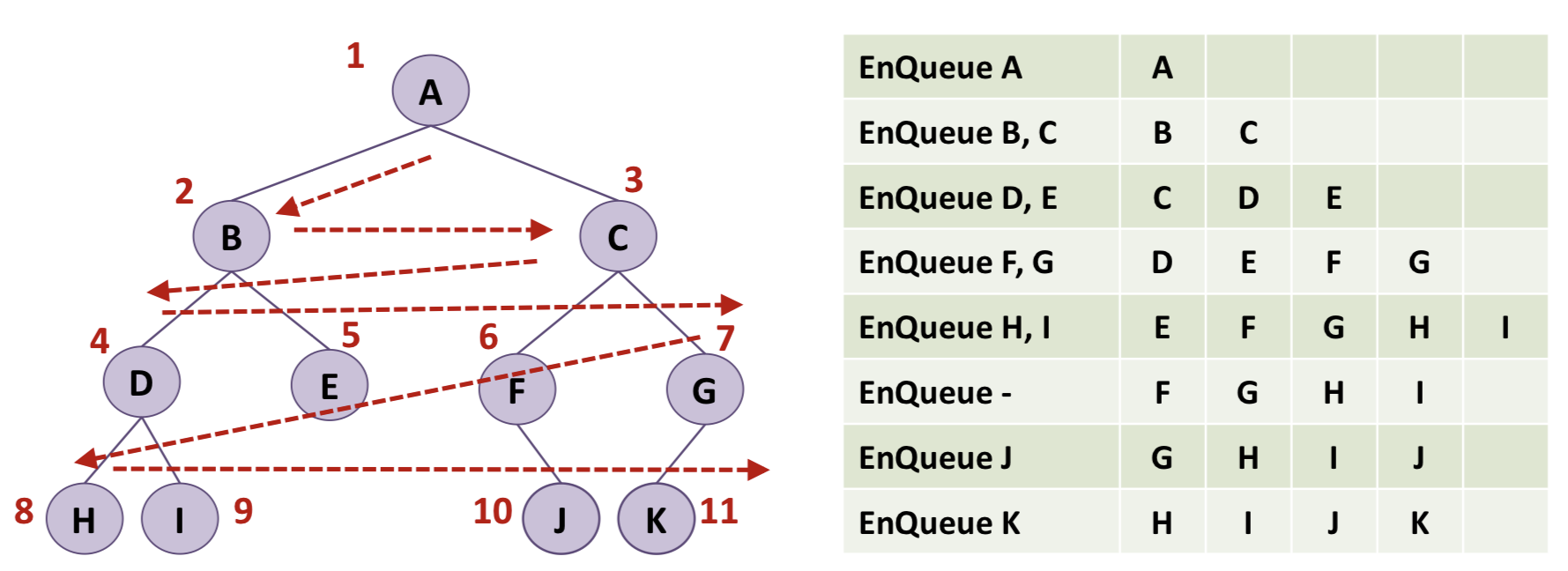
이렇게 할 수 있겠네요! 노드를 큐에서 제거할 때는 그 노드의 자식 노드를 왼쪽->오른쪽 순서로 큐에 등록합니다.
자세히 설명하자면, 차례대로 노드를 탐색 할 때 마다 탐색한 노드는 큐에서 제거합니다. 그리고 그의 자식들을 큐에 등록함으로써 순서대로 순회를 하게 되는 것입니다.
코드를 작성 해보자면 이렇게 되겠네요.
(큐를 정의하는 것은 생략합니다.)
void Levelorder(BTreeNode* root) {
Queue queue;
if (root == NULL) return;
InitQueue(&queue);
EnQueue(&queue, root);
while(!IsEmpty(&queue)) {
root = Peek(&queue);
DeQueue(&queue);
cout << root->item << " ";
if (root->left_child != NULL)
EnQueue(&queue, root->left_child);
if (root->right_child != NULL)
EnQueue(&queue, root->right_child);
}
}이진 트리 탐색 응용
이진 트리 탐색을 응용하는 방법에 대해 써보고자 합니다.
계산식을 표기하는 방법 중 중위 표기법(Infix Notation) 에 대해서 이를 적용할 수 있겠습니다.
중위 표기법이란
일반적인 수식의 표기법으로, 두 개의 피연산자 가운데에 연산자가 있는 구조입니다. X+Y 이런 식으로요!
예를 들어서 (7+4)*2-1 이라는 수식을 이진 트리로 만들어보면 다음과 같습니다.
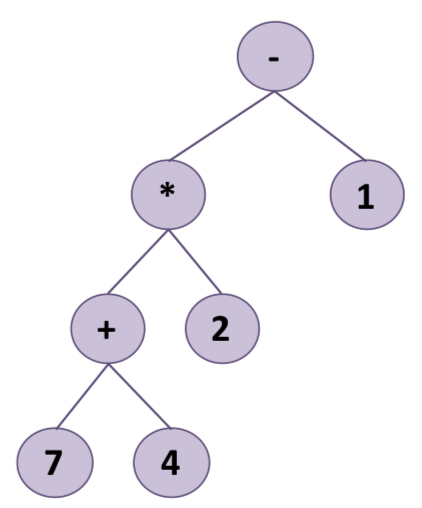
이렇게 직관적인 형태로 표현이 가능합니다.
이걸 계산하는 원리에 대해서 설명하자면 우리가 위 계산식을 계산하는 과정과 같습니다.
1. 7 + 4 를 계산합니다.
2. 위의 계산 결과를 * 노드의 왼쪽 자식 노드로 지정합니다.
3. 11 * 2 를 계산합니다.
4. 위의 계산 결과를 - 노드의 왼쪽 자식 노드로 지정합니다.
5. 22 - 1 를 계산합니다.
6. 끝!
이걸 또 코드로 표현해보자면..
코드
int CalculateExpTree(BTreeNode* root) {
int op1, op2;
if (root == NULL) return 0;
if (root->left_child != NULL && root->right_child != NULL)
return root->item; // 최종 계산 결과를 반환합니다.
op1 = CalculateExpTree(root->left_child);
op2 = CalculateExpTree(root->right_child);
switch (root->item) {
case '+': return op1 + op2;
case '-': return op1 - op2;
case '*': return op1 * op2;
case '/': return op1 / op2;
}
return 0;
}아까 작성한 트리를 탐색하는 기본 원리인 재귀적 방법을 활용하면 됩니다.
