[Jungle] Week2. 이진트리 | B-Tree

somi·2024년 3월 28일

[Krafton Jungle]

목록 보기

14/68

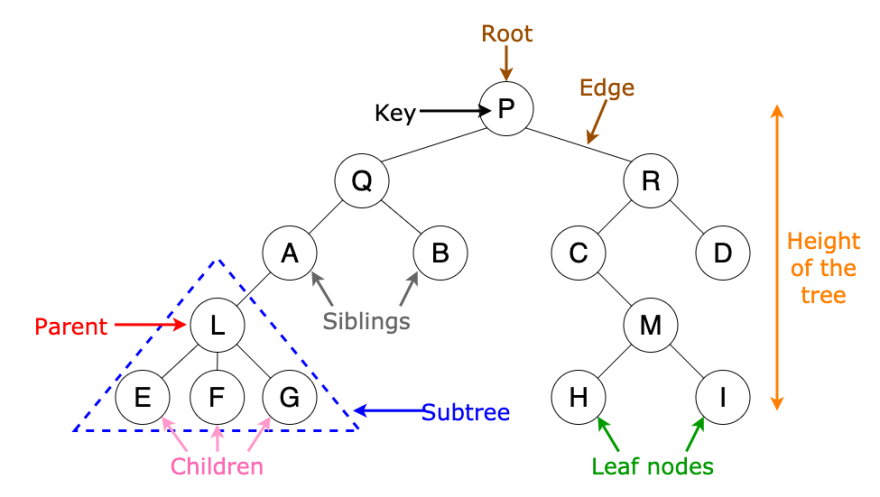
이진트리(binary tree)

모든 노드들이 2개 이하의 자식을 가진 트리

이진 탐색 트리(Binary Search Tree, BST)

각 노드는 최대 두 개의 자식 노드

왼쪽 서브 트리의 모든 노드는 부모 노드보다 작은 값

오른쪽 서브 트리의 모든 노드는 부모 노드보다 큰 값

중복 값 허용 x

장점)

구조가 단순

중위 순회의 DFS를 통하여 노드값을 오름차순으로 얻을 수 있다.

이진 검색과 비슷하게 아주 빠르게 검색할 수 있다.

노드를 삽입하기 쉽다

이진탐색 트리는 최악의 경우 균형이 한쪽으로 쏠리게 된다.

최악의 경우 계속 선형 탐색을 하게 되면 O(N) 시간이 들게 된다.

B-tree => balanced. 균형잡힌 다진 검색 트리
왼쪽 서브트리와 오른쪽 서브 트리의 균형을 유지하도록 하여 적정 깊이를 유지하도록 한다.
다진검색트리 = 왼/오 2가지로 뻗어가는 이진트리와 다르게 여러 갈래로 나뉘는 트리. Key를 기준으로 뻗어간다.

B-Tree => 이진 트리를 확장해 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 트리 구조. 다수의 키를 보유할 수 있는 트리

B-Tree

효율적인 탐색 및 삽입/ 삭제 성능. DB, 파일 시스템에서 널리 쓰이는 트리 자료구조. 말단 노드를 제외한 모든 노드는 2개 이상의 자식 구조를 가짐

이진 트리를 확장해서 더 많은 수의 자식을 가질 수 있게 일반화

각 노드는 키(key) 값과 연관된 값(value)을 가지고 있다.
왼쪽 서브트리에 속한 모든 노드의 키 값은 해당 노드의 키 값보다 작다. 오른쪽 서브트리에 속한 모든 노드의 키 값은 해당 노드의 키 값보다 크다.
시간 복잡도 O(log n) => 데이터 탐색뿐 아니라, 저장, 수정, 삭제에도 항상 O(logN)

B-Tree 탐색 연산

루트 노드로부터 위-> 아래로 탐색
해당 노드의 Key에 없으면 찾는 값이 속한 포인터의 자식 노드를 탐색

B-Tree 삽입 연산

삽입에 적절한 리프 노드를 찾아 삽입
필요한 경우 노드 분할
해당 리프 노드의 키 개수가 가득 찬 경우 - 중앙값기준으로 분할한 뒤 중앙값은 윗 레벨로 편입

-> 중앙값인 6을 부모 노드로 올리고, 5와 7분리

중앙값 6을 기준으로 3과 8분리

B-Tree 삭제 연산

삭제할 key 삭제
삭제 후 최소 Key의 수 ([m/2 (올림)]-1) 보다 작으면 같은 레벨로부터 키를 받아온다.
같은 레벨에서 지원받지 못하면, 부모 레벨에서 키를 채운다.

B-Tree
: 디스크 기반의 데이터 베이스 시스템에서 주로 사용
노드에 접근하는 시간은 보조 기억 장치인 하드디스크의 읽기 속도에 의해 결정
노드 하나에 더 많은 자식 노드를 갖도록 설계 -> 노드 하나를 읽을 때 디스크 i/o 횟수를 최소화.

비교

순차 탐색(Full scan) => 탐색 성능 O(N)
기본적으로 인덱스는 데이터의 읽기 속도를 높여야하므로 적합하지 않다.

해시 테이블: 해시 함수를 통해 나온 값을 이용하면 저장된 메모리에 바로 접근할 수 있기 때문에 O(1)의 시간 복잡도 - 특정 요소에 대한 탐색이 빠르다.
그러나 DB에서는 부등호(<, >)도 사용하기에 적합하지 않다. 시간 복잡도 O(1)의 장점을 사용하기 어렵기 때문

이진 탐색 트리(BST)

불균형적인 이진 탐색 트리의 시간복잡도는 최악의 경우 O(N), balanced BST의 경우 최악의 경우 O(logN)

Red black Tree: 하나의 노드가 가지는 데이터 개수가 딱 하나
트리에 원소가 n개 있을 때 삽입/삭제/검색 O(logn)

-> b-tree는 각 노드마다 배열을 가짐. 같은 노드 공간의 데이터들끼리는 굳이 자식 노드에 접근할 때처럼 참조 포인터 값으로 접근할 필요 없음. -> 대량의 데이터 처리할 때 하나의 노드에 많은 데이터를 가질 수 있다는 장점