트라이(Trie)
문자열에서의 검색을 빠르게 해주는 자료구조.
순차탐색이 아닌 트리로 접근하기 위해 만들어진 자료구조
주로 prefix tree, digital search tree, retrieval tree -> Trie
단순 비교
전체 문자열의 맨 처음부터 끝까지 개별 문자 비교
-> 최대 문자열 길이 m, 전체 문자 개수 n개 => 최악O(nm)이진 탐색 기법
전체 문자열을 사전 순으로 배열 저장 후 중간 값과 비교해서 좌/우 반으로 비교하는 방식 반복
-> 최대 문자열 길이 m, 전체 문자 개수 n개 => 정렬 O(nmlogn), 탐색 O(mlogn) => O(nmlogn)정렬)
n개의 문자열 정렬 -> O(nlogn)
각 문자열은 최대 m개의 문자 => O(nmlogn)
탐색)
배열의 중간값과 검색 대상 비교 -> 각 단계마다 복잡도 O(logn)
최대 m번의 문자열 비교 -> O(mlogn)

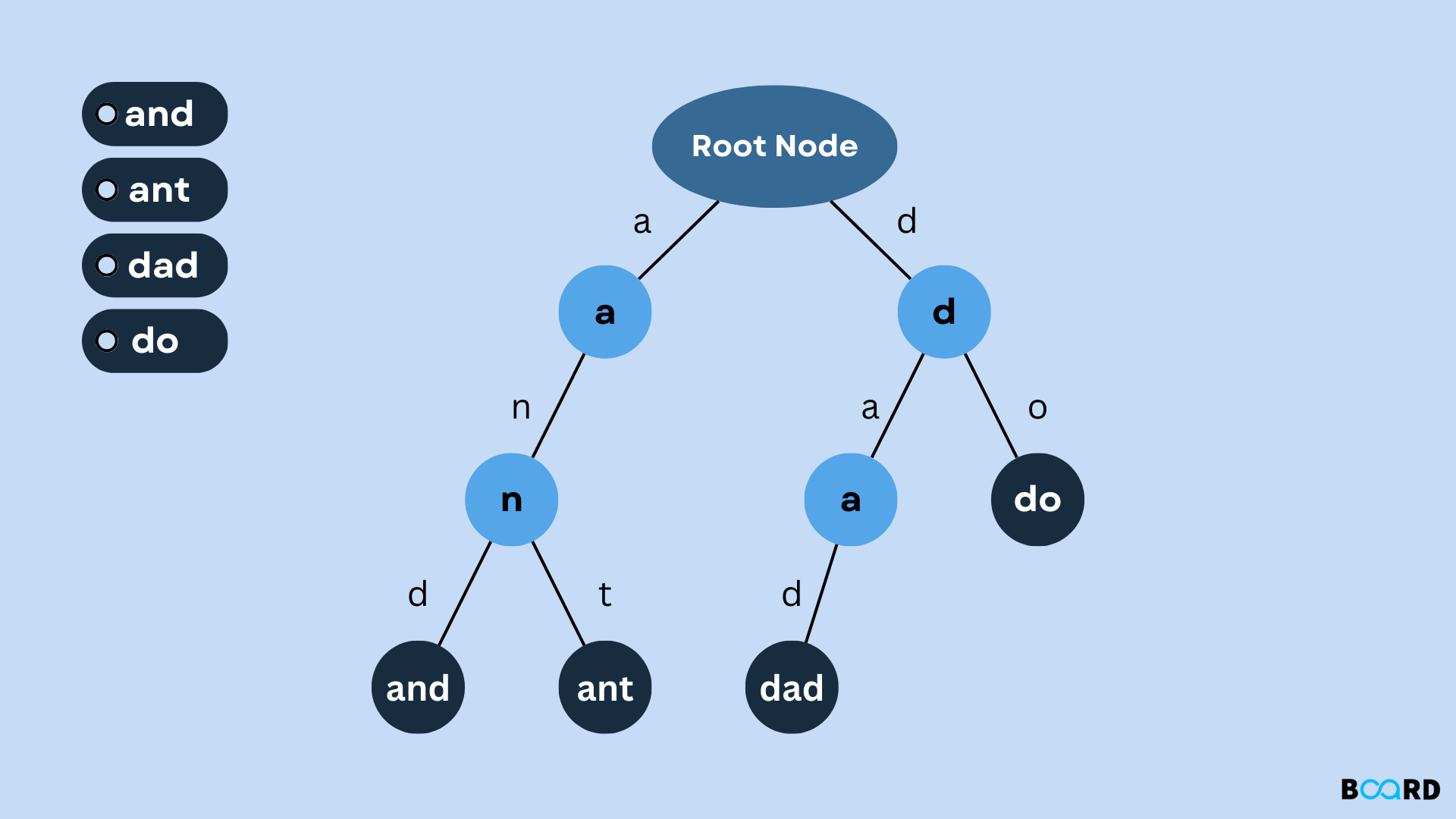
- 자동완성, 사전 검색을 할 때 특화된 자료구조
- 문자열 탐색시 하나씩 비교하지 않고 key로 노드 탐색 -> 효율적
- 그러나 각 노드에서 자식들에 대한 포인터를 배열로 모두 저장 -> 저장 공간 크기가 크다.
- 키의 길이가
m일때 탐색과 삽입 모두O(m)시간
탐색 - 키 문자열과 연관된 값 반환
삽입 - 문자열(키)와 그 값 삽입
class Trie:
def __init(self):
self.trie = {}
def insert(self, word):
t = self.trie
for c in word:
if c not in t:
t[c] = {}
t =t[c]
t['*'] = True
def search(self, word):
t = self.trie
for c in word:
if c not in t:
return False
t = t[c]
return '*' in t
def startsWith(self, prefix):
t = self.trie
for c in prefix:
if c not in t:
return False
t = t[c]
return True 트라이

장점)
특정 접두사를 가진 문자열 검색에 효율적
트라이 -> 키를 사전식으로 정렬된 순서로 저장. 문자별로 트리가 만들어지기 때문에 자동적으로 정렬
사전 순으로 순회하거나 특정 접두어를 가진 모든 키를 찾는 것 용이
완전히 일치하는 문자열이 아니라 일부를 생략하더라도 탐색이 가능함
단점)
대규모 데이터에 대해서는 메모리 소비가 크다.
트라이의 각 노드는 가능한 다음 문자에 대한 포인터를 가지기 때문에 문자열의 길이에 따라 메모리 사용량 증가
트라이는 삽입과 삭제 연산이 비교적 복잡
트라이와 다른 자료구조와의 비교

배열
- 삽입/삭제일 경우 원소를 한칸씩 전부 이동해야 하기에 매우 비효율적
- 배열 크기를 증가시키거나 축소시켜야하는 경우가 발생할 수 있다.
- 구현하기 쉽고 포인터의 저장공간이 필요없다는 장점
반면 트리 구조는 참조(포인터)만 변경해주면 된다!
-> 원소의 대량 이동이 필요 없다.
연결 리스트
- 트라이보다 검색, 삭제, 삽입 분야에서 취약
- 연결 리스트에 단어 하나를 담을 때 시간 복잡도 O(n) -> 여러개를 담으면 그 배수만큼 늘어날 것
해쉬 테이블
- 평균적으로 매우 빠른 검색 및 삽입 시간. 해시 함수를 사용하여 데이터의 위치를 계산하기 때문에
O(1)의 시간 복잡도
해쉬함수가 이상적이면 O(1), 최악의 경우 검색 시간 O(N)이 될 수 있음 - 그러나 해쉬 충돌이 발생할 수 있다.
- 데이터가 해쉬 함수의 결과에 의해 직접적으로 저장 - 정렬이나 순서 유지하기가 어려울 수도 있다.
트라이는 해시 테이블보다 공간 효율성이 낮을 수도 있다. 트라이는 문자열을 각각 문자 단위로 분리해서 저장 -> 문자열의 길이가 길면 트라이 깊이가 깊어진다.
참고)
https://butter-shower.tistory.com/217
https://hongjw1938.tistory.com/24
https://velog.io/@joon6093/%ED%94%84%EB%A1%9C%EC%A0%9D%ED%8A%B8%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%9D%BC%EC%9D%B4C%EC%96%B8%EC%96%B4-%EA%B5%AC%ED%98%84%EB%8B%A8%EA%B3%84
