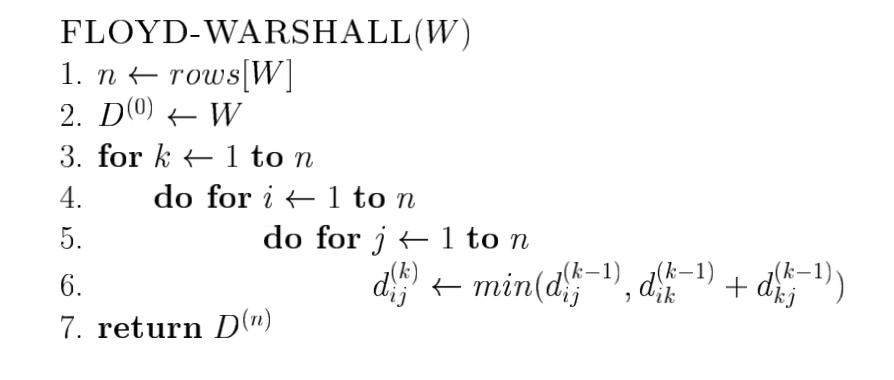[Jungle] Week2. (최단경로) 다익스트라 | 플로이드 와샬 알고리즘

다익스트라(Dijkstra) 알고리즘

하나의 출발점에서 다른 특정 지점까지의 최단 경로
시작 정점부터 시작하여 해당 정점까지의 최단 경로를 갱신하며 진행.
그래프 간선의 가중치가 음수가 아니여야 한다.
미방문 정점 중 현재까지의 최단 경로가 가장 짧은 정점을 선택해서 방문하고 이를 통해 각 경로를 계산
우선순위 큐/힙를 일반적으로 사용

import heapq

def dijkstra(graph, start):
    distances = {node: float('inf') for node in graph}
    distances[start] = 0
    queue =[]
    heapq.heappush(queue, [distances[start], start])

    while queue:
        current_distance, current_node = heapq.heappop(queue)

        if distances[current_node] < current_distance:
            continue

        for adjacent, weight in graph[current_node].items():
            #현재 정점  + 인접한 정점 계산 
            distance = current_distance + weight

            #현재까지의 최단 거리보다 더 짧은 경우 업데이트 
            if distance < distances[adjacent]:
                distances[adjacent] = distance
                heapq.heappush(queue, [distance, adjacent])

        return distances 

각 정점마다 최단 경로의 비용 저장

시간복잡도 : 인접행렬 - O(V^2)
인접리스트 = 우선순위 큐로 구현하면 O(ElogV)

플로이드 와샬(Floyd-Warshall) 알고리즘

모든 정점 쌍 사이의 최단 경로를 찾는 동적 프로그래밍 알고리즘
모든 정점 쌍 사이의 최단 경로를 갱신하는 과정을 반복하여 모든 정점 쌍 사이의 최단 경로를 계산
보통 2차원 배열을 사용하여 최단 경로 저장
다익스트라 알고리즘과 달리 음의 간선도 사용 가능 - 다익스트라 알고리즘에 비해 상대적으로 시간이 더 많이 소요된다.
두 정점 간의 최단 경로의 길이를 저장
시간복잡도 O(N^3)-> 3중 for 문

예시 코드

import sys
input = sys.stdin.readline

N = int(input())
M = int(input())

INF = int(1e9)
cost = [[INF]*(N+1) for _ in range(N+1)]

print(cost)
#자기 자신으로 가면 0 으로 초기화
for i in range(N+1):
    for j in range(N+1):
        if i ==j:
            cost[i][j] = 0
for _ in range(M):
    a, b, c = map(int, input().split())
    cost[a][b] = min(c, cost[a][b])


#플로이드 와샬
for k in range(N+1): #중간 노드
    for i in range(N+1): #처음 노드
        for j in range(N+1): #마지막 노드
            cost[i][j] = min(cost[i][j], cost[i][k] + cost[k][j])

for i in range(1, N+1):
    for j in range(1, N+1):
        if cost[i][j] == INF:
            print(0, end = " ")
        else:
            print(cost[i][j], end = " ")
    print()

풀어보기)

다익스트라 - 백준 1753 최단 경로
플로이드 와샬 - 백준 11403 경로 찾기