[Jungle] Week2. 최소 비용 신장 트리(프림, 크루스칼)

신장트리(spanning tree)

• 그래프 G의 모든 정점과 간선의 일부(또는 전부)를 포함하는 트리
  
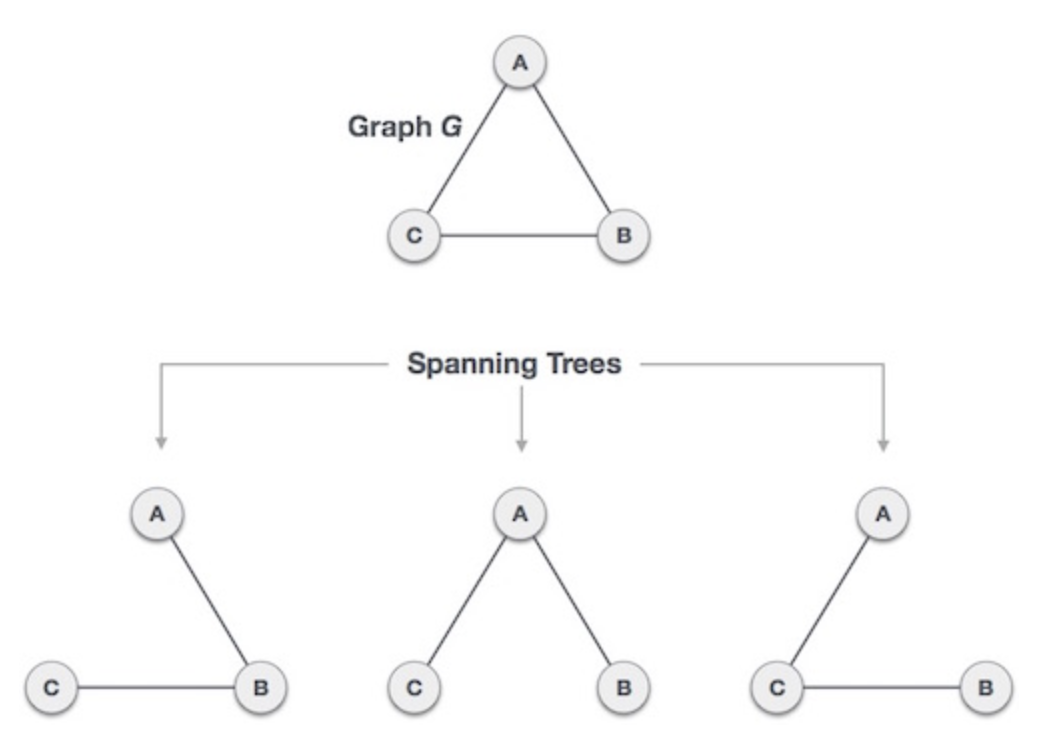
  하나의 그래프가 있을 때, 모든 노드를 포함하면서 즉 모든 노드들 간에 서로 연결은 되어있지만 사이클은 존재하지 않는 부분 그래프

최소 비용 신장 트리

: 가중치 그래프 G의 가중치가 작은 간선을 선택하여 구성된 신장 트리

프림 알고리즘(Prim's algorithm)

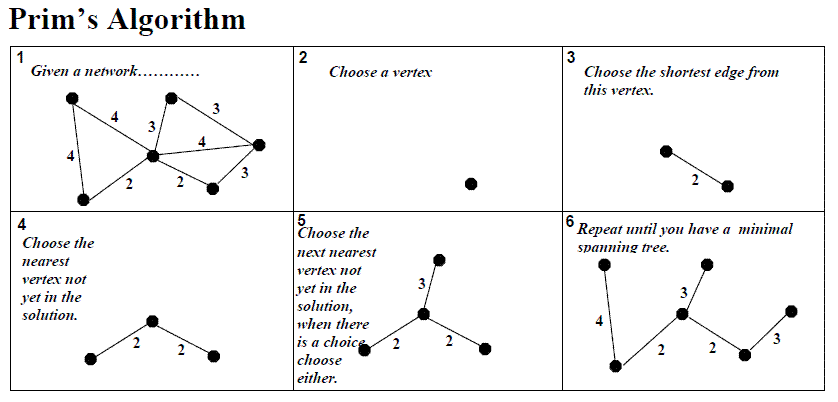
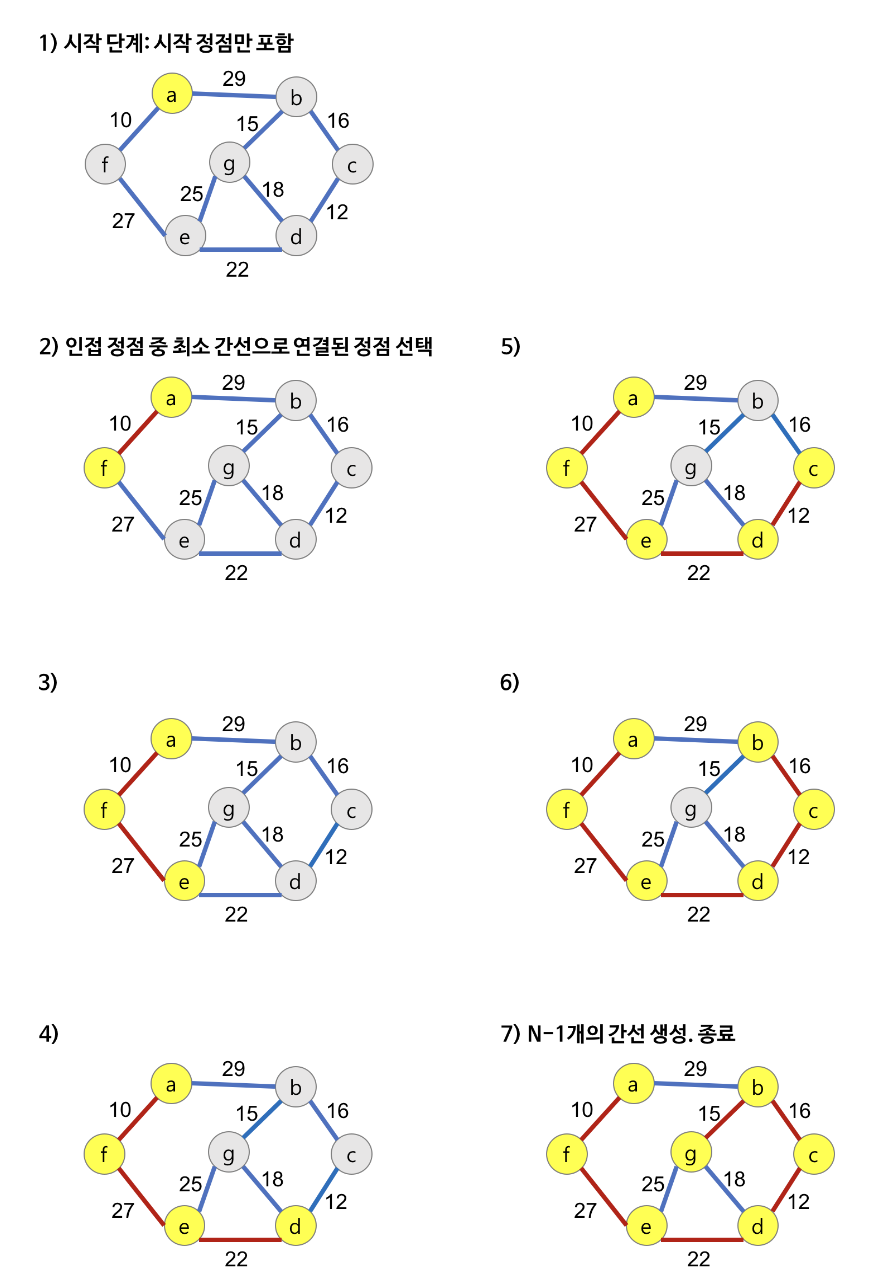
그래프 전체에서 최소 비용을 갖는 간선 {u, v}를 선택하여 이 간선을 최소 비용 신장 트리 T에 추가함
이 간선을 최소 비용 신장 트리 T에 추가하였을 때 사이클을 형성하지 않으면 T에 추가 아니면 무시하지 않으면 그 간선을 선택함

def prim(start, weight):
    visit = [0]*(V+1)
    q=  [[weight, start]]
    ans = 0
    cnt = 0
    while cnt < V:
        k, v = heappop(q)
        if visit[v]:
            continue
        visit[v] =1
        ans +=1
        cnt +=1
        for u, w in G[v]:
            heappush(q, [w,u])
    return ans

크루스컬 알고리즘(Kruskal's algorithm)

남은 간선 중에서 무조건 최소 비용인 간선을 선택한 후 사이클을 형성하지 않으면 그 간선을 선택함

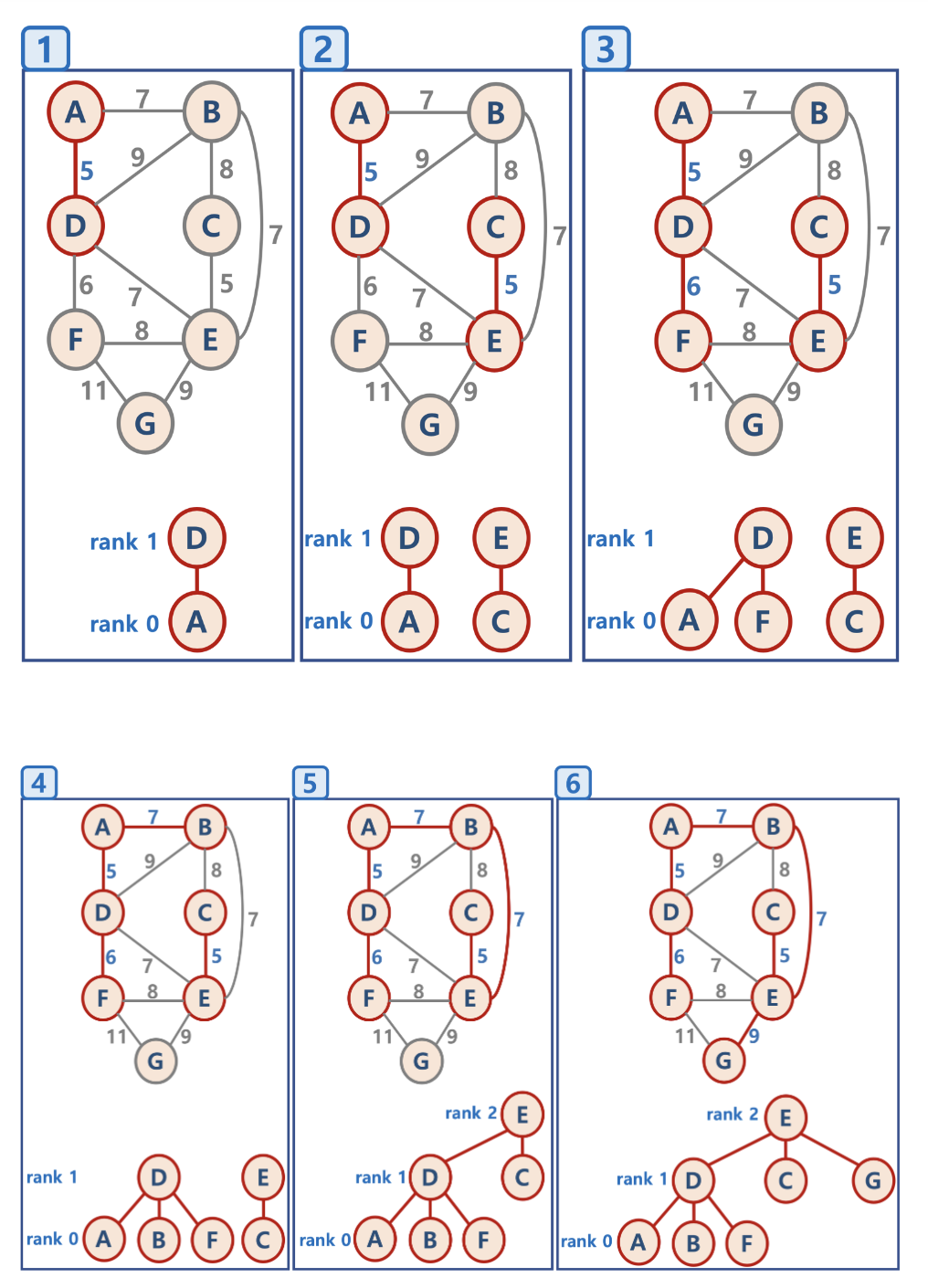
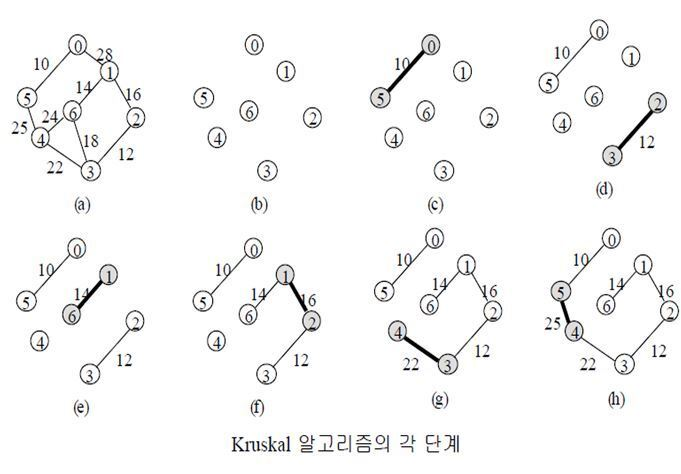
• 간선들의 가중치 오름차순으로 정렬
• 가중치가 작은 간선부터 사이클 형성하는지 검사
• 사이클 형성하지 않는 간선만 포함

참고)
https://gmlwjd9405.github.io/2018/08/30/algorithm-prim-mst.html
https://velog.io/@jxlhe46/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-MST
https://techblog-history-younghunjo1.tistory.com/262