[Jungle] Week5. Red-Black Tree 의 삭제 연산

RB Tree 삭제 연산

• 삭제 전 RB Tree 속성 만족한 상태
• 삭제 방식은 일반적인 BST와 동일
• 삭제 후 RB트리 속성 위반 여부 확인
• RB 트리 속성을 위반했다면 재조정(delete-fixup)
• RB 트리 다시 만족

---

RB Tree에서 속성 위반 여부 판단: 노드를 삭제할 때 어떤 색이 삭제되는지를 통해! ! !

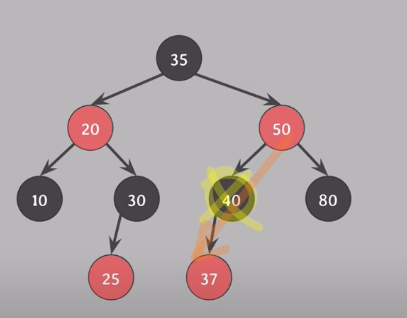
삭제하려는 노드의 자녀(유효값을 가지는)가 없거나 하나라면 삭제되는 색 => 삭제 되는 노드의 색

25 삭제 => red 삭제
80 삭제 => black 삭제
40 삭제 => black 삭제

---

삭제하려는 노드의 자녀가 둘이라면 삭제되는 색 = 삭제되는 노드의 Successor의 색!

successor: 오른쪽 서브트리의 가장 작은 값

20 삭제 => successor 25 삭제 -> red 삭제
35 삭제 => successor 37 삭제 -> red 삭제
50 삭제 => successor 80` 삭제 -> black 삭제

삭제되면서 기존의 색깔은 successor가 물려받게 되니까 successor의 색깔이 삭제되는 것이다.

---

삭제되는 색이 Red라면

어떠한 속성도 위반하지 않는다.

1. 모든 노드는 Red or black
2. 루트 노드는 black
3. 모든 nil 노드는 black
4. 노드가 red라면 자녀들은 black.
   : 레드는 연속으로 나오지 못한다.
5. 임의의 노드에서 그 노드의 자손 nil 노드들까지 가는 경로들의 black수는 같다.
   : 레드는 영향을 주지 못하니 #5번 속성에도 영향 x

삭제되는 색이 Black이라면?

#2, #4, #5번 속성을 위반할 수 있다.

2. 루트 노드는 black
3. 노드가 red라면 자녀들은 black.
4. 임의의 노드에서 그 노드의 자손 nil 노드들까지 가는 경로들의 black수는 같다.

• black이 지워졌을 때 블랙 높이는 -1이 됨 #5 속성 깨짐

---

delete-fixup 삭제시 속성 위반 재조정하기

삭제되는 색이 Black일 때 #2 위반 해결하기

(#2: 루트 노드는 black 속성) 위반 해결하기

=> 루트 노드를 black 으로 바꾸면 된다.

---

삭제되는 색이 Black일 때

특수한 상황을 제외하면 #5 속성을 항상 위반하게 된다.

(#5: 임의의 노드에서 그 노드의 자손 nil 노드들까지 가는 경로들의 black 수는 같다.)

#5 속성을 다시 만족시키기 위해 삭제된 색의 위치를 대신하는 extra black을 부여한다.

경로에서 black 수를 카운트할 때 extra black은 하나의 black으로 카운트된다.

어디에 extra black을 부여해야 하는가?

삭제된 색의 위치를 대체한 노드!

: 10의 위치를 대체한 nil 노드에 extra black 부여 => #5 속성 다시 만족 doubly black

---

red-and-black : extra black이 부여된 red 노드

---

doubly black

삭제되는 색이 black이고 #5 위반일 때

extra black을 부여받은 노드는

doubly black이 되거나 red-and-black이 된다.

---

extra black 부여 후에

red-and-black 해결하기

red-and-black을 black으로 바꾸면 해결된다.

---

doubly black 노드 해결 하기

어떤 extra black을 어떻게 없앨 것인지가 관건

총 4가지 Case -> doubly black의 형제의 색과 그 형제의 자녀들의 색으로 분류

case4

---

case 3

---

case2

---

case 1

---

정리_ 삭제되는 색이 black일 때 #5 위반 해결하기

삭제 되는 색이 black일 때, 삭제되는 색이 있던 위치를 대체한 노드에 extra black 부여
대체한 노드가 red-and-black이 됐다면 black으로 바꿔주면 끝
대체한 노드가 doubly black => case 1, 2, 3, 4 로 해결

---

Red black trees - Deletions

1. transplant
   : helps us move subtrees within the tree
2. delete
   : deletes the node
3. delete_fixup
   : fixes any red-black violations

RB- Trnasplant(T, u, v)

RB- Delete(T, z)

RB-Delete-Fixup(T,x)

Insert-Fixup(T, z): z - 새로 들어온 노드
Delete-Fixup(T, x) : x - 삭제된 z를 대체하는 노드

++

최종 정리

red-and-black은 그냥 black으로 바꿔주면 되기 때문에
삭제연산에서 중요한 것은 doubly-black을 어떻게 해결할 것인지가 중요하다.

case 4

doubly black 의 오른쪽 형제 노드 black, 형제의 오른쪽 자식이 red
doubly black 의 왼쪽 형제 노드 black, 형제의 왼쪽 자식이 red

w.color = x.p.color 
//형제노드의 색상을 부모 노드의 색상으로 변경 
x.p.color = BLACK // 부모 노드 색을 black으로
w.right.color= BLACK //형제노드의 오른쪽 자식을 검은색으로
LEFT-ROTATE(T, x, p) // 이진탐색트리 T에서, x의 부모 노드 p를 기준으로 왼쪽 회전 

---

case 3

doubly node 오른쪽 형제 노드가 black, 형제의 왼쪽 자식이 red
doubly node 왼쪽 형제 노드가 black, 형제의 오른쪽 자식이 red

w.left.color = BLACK //형제 노드의  왼쪽 자식 색 검은 색 변경 
w.color = RED
RIGHT-ROTATE(T,w)
w = x.p.right

이하 CASE 4

---

case 2

doubly node 오른쪽 형제 노드가 black, 형제의 왼/오 자식 모두 black
doubly node 왼쪽 형제 노드가 red, 형제의 왼/오 자식 모두 black

//형제노드 w의 양쪽 자식 노드 모두가 검은색
if w.left.color == BLACK && w.right.color = BLACK
	//형제 노드의 색을 RED로 바꾸고 
    //X가 이제 부모 노드를 가리키도록 업데이트 
    w.color = RED
    x= x.p
...
=> 트리의 균형을 맞추기 위해 다른 케이스로 이동이 가능해진다. 

---

case 1

doubly node 형제가 red인 경우

if w.color == RED
//x의 형제 노드 w를 검은색으로 변경
	w.color = BLACK
    //x의 부모 노드의 색 Red로 변경
    x.p.color = RED
    x.p를 기준으로 왼쪽 회전 
    LEFT-ROTATE(T, x, p)
    w= x.p.right 

---

삽입 연산도 쉽지는 않았지만 rb tree 삭제연산 너무 어렵다.
self balancing tree의 이점 (시간 복잡도 면에서도 좋은 건 알겠지만) 삭제의 경우 이걸 c 언어로 어떻게 구현할 수 있는지 감이 잡히지 않는다.
doubly black과 red-and-black을 실제 코드로 구현하고 case 1, case 2, case 3, case 4를 pusedo code 참고해서 구현하면 되는 것인가,,,,,