[Jungle] Week5. Red-Black Tree 와 AVL Tree

Red-Black Tree

• binary search tree: yes
• 삽입/삭제/검색 시간 복잡도: worst case에서도 O(log N)
• 삽입/삭제 성능: AVL 트리에 비해 빠르다.
• 검색성능: AVL 트리에 비해 느리다.
• 균형 잡는 방식: red-black 트리 속성을 만족시키도록
• 응용 사례: Linux kernel 내부에서 사용, java treemap 구현, c++ std::map 구현 등등

AVL Tree

=> 또한 스스로 균형을 잡는 트리

• balance factor를 통해 균형 유지
• 노드의 balance factor: 임의의 노드 x에 대해서 Balance Factor => BF
  BF(x) = h(lSubtree(x)) - h(rSubtree(x))
  

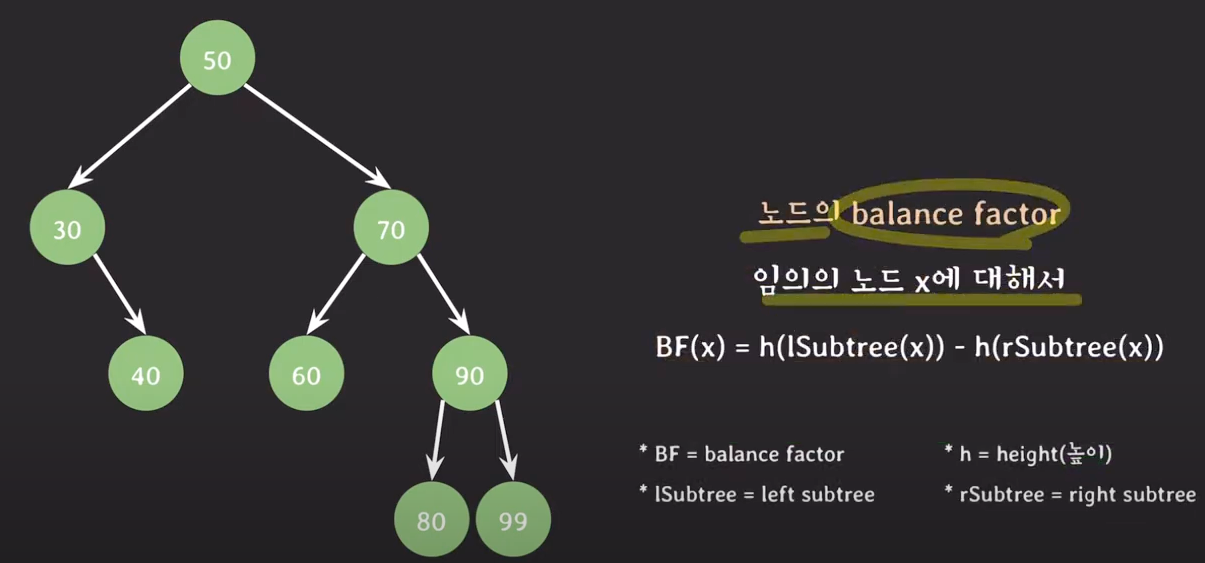
50에서의 bf => 1 - 2 = -1

AVL 트리의 삽입/삭제 후

: BF(x) 가 {-1, 0, 1} 이 아닌 노드가 생기면 균형을 맞추는 작업 수행

• binary search tree: yes
• 삽입/삭제/검색 시간 복잡도: worst case에서도 O(log N)
• 삽입/삭제 성능: Red-black 트리에 비해 느리다.
• 검색 성능: Red-black 트리에 비해 빠르다.
• 균형 잡는 방식: balance factor => {-1, 0, 1} 이 되도록
• dictionary, 한번 만들어 놓으면 삽입/삭제가 거의 없고 검색이 대부분인 상황에서 사용

AVL 트리는 각 노드 삽입/삭제 후 균형 맞추기 작업을 위해 rbtree 보다 더 잦은 회전 연산
RB 트리는 각 노드에 색상 정보만 추가하면 되지만 AVL 트리는 더 많은 추가 데이터 (높이 정보 등) 을 필요로 한다.

AVL 트리는 적은 수의 요소를 가진 데이터 요소에 적합,
RB 트리는 데이터를 동적을로 추가 제거하는 작업이 빈번하게 발생하는 상황 -> 데이터 베이스 인덱스에서 더 적합하다.

왜 RB TREE가 AVL 트리보다 많이 쓰일까??

두 트리 모두 시간 복잡도는 O(log N) 이지만
AVL 트리가 밸런스를 더 엄격하게 유지한다. -> 따라서 RB Tree는 AVL 트리에 비해 탐색엔 불리하지만 삽입과 삭제 연산에 대해서는 상대적으로 더 유리하다.

현실 프로그램에서는 데이터의 삽입과 삭제가 빈번하게 일어나므로 RB Tree가 더 많이 쓰이게 된다.