메모리의 구조
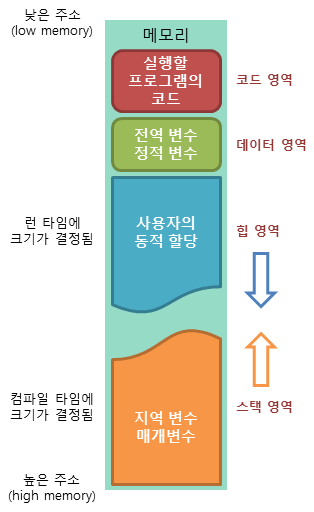
스택, Stack
스택: 프로시저 호출 시 지역변수와 매개변수를 저장하기 위한 메모리 공간. 선언되는 순서와 반대로 메모리가 해제되는LIFO(Last in First Out) 후입 선출구조함수의 로컬 변수 저장: 각 함수 호출 시 그 함수의 로컬 변수들이 스택에 저장함수의 제어 흐름 관리: 함수가 다른 함수를 호출할 때 반환 주소와 이전 함수의 스택 프레임이 스택에 저장- 동적으로 메모리를 할당하고 해제할 수 있다.
- 구현이 간단하며 메모리 관리 오버헤드가 낮다.
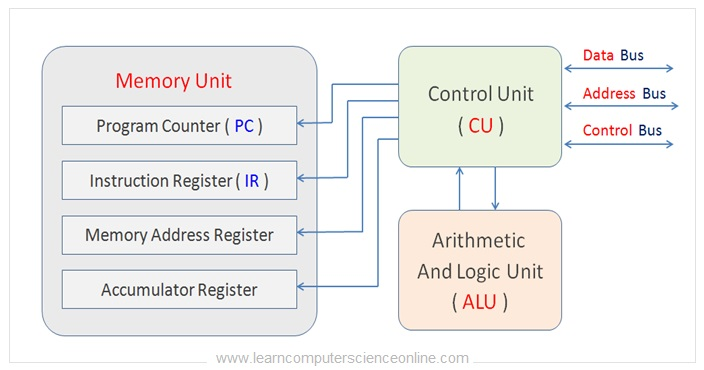
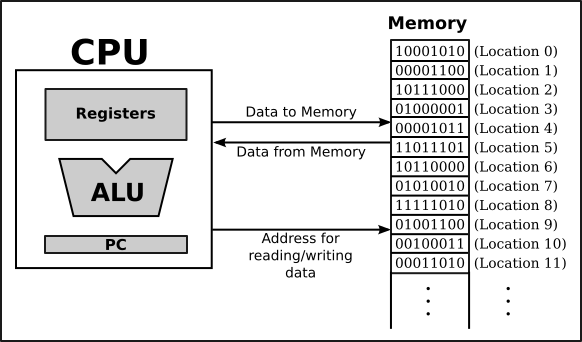
레지스터, register
- 프로세서 내부의 고속 작동 메모리, 프로시저 실행 중 자주 접근하는 변수나 중간 계산값을 저장하기 위해 사용된다
- 중간 연산 결과의 저장: 연산 중 생성되는 중간 값을 빠르게 저장하고 접근하기 위해 사용
- 빠른 데이터 접근: 특정 데이터나 주소를 빠르게 저장하고 로드하기 위해 사용
- 매우 높은 데이터 접근 속도를 제공
- 데이터를 메모리로부터 레지스터로 빠르게 이동시킬 수 있어서 연산 효율 증가
메모리 할당
정적할당(Static Allocation): 변수선언을 통해 필요한 메모리를 확보하는 방법.
프로그램이 실행되기 전인컴파일시간에 변수 또는 배열에 메모리 할당. 프로그램이 실행되기 전에 메모리의 크기와 위치가 결정됨.
빠른 속도로 간편하게 사용할 수 있지만, 프로그램 실행 중에 크기를 변경할 수는 없고, 필요지 않은 경우에도 계속 메모리를 차지한다.
동적할당(Dynamic Allocation): 프로그램 실행 도중 필요한 메모리를 확보하는 방법. 프로그램에 필요한 메모리의 크기와 위치를 동적으로 조정 가능.
높은 유연성, 효율적인 메모리 사용 가능 but, 메모리 할당/해제 과정에서 오버헤드가 발생할 수 있고, 메모리 누수나 해제된 메모리에 대한 포인터 역참조 등의 문제 발생 가능
재귀 함수의 단점
-> 함수 호출 시 메모리가 추가적으로 사용돼 메모리 소비가 많고 잚소 사용하면 스택 오버플로우 발생. 반복문에 비해 빈번한 스택 메모리 할당/해제로 실행 속도가 느릴 수 있다.
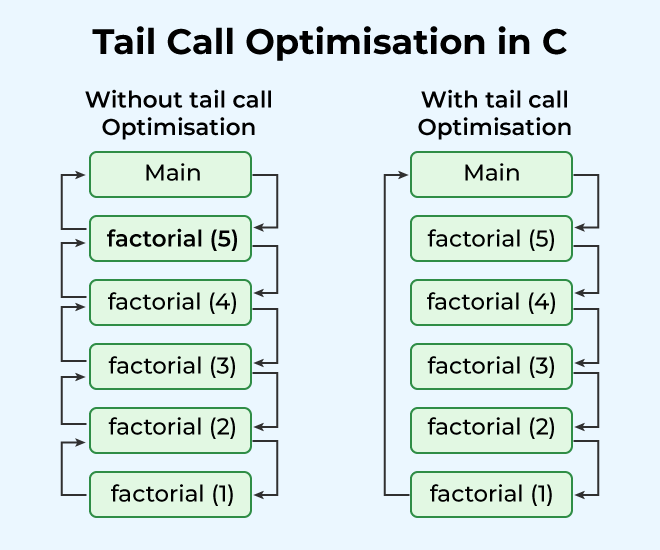
꼬리 재귀 최적화, Tail Recursion Optimization
꼬리 재귀 최적화는 재귀 함수 호출시 호출 스택의 사용을 최적화하는 기법
재귀 함수는 호출될 때마다 스택 프레임이 생성되며 이는 메모리 사용량 증가와 스택 오버플로우의 원인이다. 꼬리 재귀 최적화는 재귀 함수의 마지막 연산만 호출 스택에 남겨두고 나머지를 제거한다.
이를 통해 함수가 반환될 때 호출 스택을 재사용할 수 있다.
꼬리 재귀 함수는 반환값을 바로 return하기 보다는 파라미터로 전달. -> 호출 스택에 쌓이지 않고 후속 호출로 이동된다. 마지막 호출에서 스택 프레임을 재활용하므로 메모리 사용량이 일정하게 유지된다
일반 재귀 함수는 추가 연산이 존재하지만, 꼬리 재귀는 재귀 호출이 끝나고 현재 함수에서 추가 연산 필요하지 않도록 구현.
꼬리 재귀 -> 함수 호출이 반복될 때 스택이 깊어지는 문제를 컴파일러가 선형으로 처리하도록 알고리즘을 바꾸기 때문에 스택을 재사용할 수 있다.
하지만 컴파일러가 꼬리 재귀 최적화를 지원하지 않는다면 일반 재귀처럼 돌아간다.
일반 재귀int factorial(int n){ if (n==1) { return 1; } return n*factorial(n-1); }
꼬리 재귀 최적화를 구현한 경우int factorialTail(int n, int acc) { if (n==1) { return acc; } return factorialTail(n-1, n*acc); }
Greedy vs. Dynamic Programming
Greedy
매 순간마다 가장 좋아보이는 선택
지역 최적화를 통해 전역 최적화를 기대
각 단계에서 최적의 해답을 찾아 나가면서 전체 문제의 최적 해답을 찾아나가는 방식. 각 단계에서의 결정은 지금까지의 상황만 고려, 이후의 상황은 고려하지 않음Dynamic Programming
복잡한 문제를 여러 개의 하위 문제로 나누어 해결하고 그 결과를 저장하여 나중에 같은 하위 문제가 다시 발생하면 저장된 결과를 사용하는 알고리즘.
중복된 하위 문제를 여러번 해결하는 것 방지하여 효율성 높임
DP
타뷸레이션(Tabulation), 상향식, Bottom-up: 작은 문제부터 차례대로 해결해 나가면서 큰 문제의 해결책 구함메모이제이션(Memoizaation), 하향식, Top-down: 큰 문제를 작은 문제로 나누어 해결한다. 필요할 때 하위 문제를 해결한다.
참고)
https://tcpschool.com/c/c_memory_structure
https://velog.io/@hyeon_zip/%EB%8F%99%EC%A0%81%ED%95%A0%EB%8B%B9-vs-%EC%A0%95%EC%A0%81%ED%95%A0%EB%8B%B9



