//열거헝 enum 선언
//두가지 상수를 가진다. -> 각 노드의 색깔을 나타냄
typedef enum { RBTREE_RED, RBTREE_BLACK} color_t;
//레드 블래 트리의 각 노드는
//정수형 키 값을 가진다.
typedef int key_t;
//노드 구조체 선언
//각 노드는 color, key_t
// 부모 노드를 가리키는 포인터 *parent,
//좌측, 우측 자식을 가리키는 포인터 *left, *right
typedef struct node_t {
color_t color;
key_t key;
struct node_t *parent, *left, *right;
} node_t;
//RB tree 구조체
//*root: 루트 노드를 가리키는 포인터
//*nil 노드를 가리키는 포인터 -
//-> 실제 데이터가 아닌 트리의 경계를 나타내는 노드
typedef struct {
node_t *root;
node_t *nil;
} rbtree;
typedef => type defined의 약자
: 새로운 이름을 기존의 데이터 타입에 할당. 새로운 자료형을 선언할 수 있음 .
typedef 재정의할 자료형 재정의된 이름
enum color_t -> typedef enum을 사용하여 코드 가독성이 더 높아졌다. 상수에 직접 숫자를 대입하는 대신 열거형을 사용 -> RBTREE_RED는 0, RBTREE_BLACK은 1로 할당.
key_t 각 노드가 가지는 정수형 키 값
node_t : 색, 키값, 부모, 왼쪽 자식, 오른쪽 자식을 가리키는 포인터
rbtree
: root, nil을 가리키는 포인터를 가진다.

rbtree *new_rbtree(void)
rbtree *new_rbtree(void) {
rbtree *p = (rbtree *)calloc(1, sizeof(rbtree));
p -> nil = (node_t *)calloc(1, sizeof(node_t));
p->root = p->nil;
p->nil->color = RBTREE_BLACK;
return p;
}
(형식 *)malloc(크기)
: c = (char *)malloc(strlen("hello") +1)
(형식 *)calloc(개수, 크기)
malloc vs. calloc
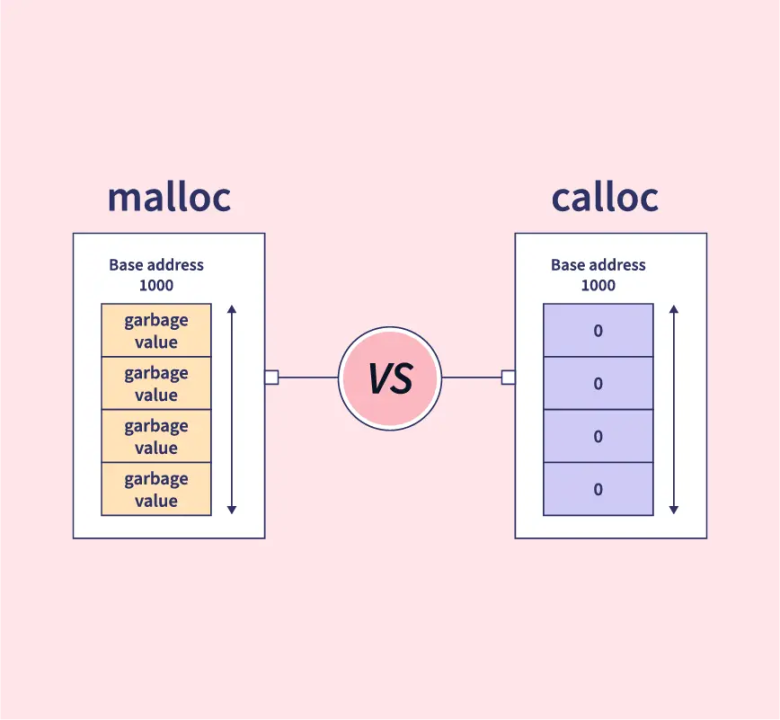
malloc
: 주어진 크기의 메모리 블록을 할당하고, 초기화하지 않은 상태로 반환
calloc
: calloc은 malloc과 달리 할당된 메모리를 0으로 초기화. 따라서 초기화된 상태의 메모리를 반환하므로 추가적인 초기화 과정이 필요 없다. 하지만 malloc의 시간이 상대적으로 더 빠를 것이다.
malloc은 쓰레기 값이 들어가지만, calloc은 0으로 초기화해준다.
RB Tree에서의 회전
회전 왜 하는가?
RB tree에서 노드를 삽입/삭제하면 RB tree의 균형을 이루기 위해 있는 5가지 속성이 위배되게 된다.
그래서 이 속성을 위배하지 않게 하기 위해 회전을 사용한다.
회전을 사용하면 이 속성을 유지하면서 트리의 구조를 변경할 수 있다.

left_rotate
node_t *y;
y = x->right; //y는 x의 오른쪽 서브트리
x->right = y->left; //y 왼쪽 서브트리를 x의 오른쪽 서브트리로 옮긴다.
//y의 왼쪽 자식이 있다면
if (y->left != t->nil) {
y->left->parent = x; //y의 왼쪽 자식의 부모 = x => 서로 연결해준다.
}
y->parent = x->parent; // x의 부모를 y로 연결한다. x-y의 연결을 끊는다.
if (x->parent == t->nil) {
t->root = y;
// x의 부모가 nil이면 (Root node이면)
// Rb tree의 루트 노드를 y로 설정
}
else if( x== x->parent->left) {
x->parent->left = y;
}
else {
x->parent->right = y;
}
// y의 왼쪽 자식 = x
// x의 부모 = y
// 서로 연결시킨다.
y->left = x;
x->parent = y;
right_rotate
오른쪽 회전은 left_rotate의 대칭으로 해준다.
node_t *y;
y = x->left; // y는 x의 왼쪽 서브트리
x->left = y->right; // y의 오른쪽 자식을 x의 왼쪽 자식으로
//y의 오른쪽 자식이 있다면
if (y->right != t->nil) {
y->right->parent = x; //y의 오른쪽 자식의 부모 = x
}
y->parent = x->parent ; // x의 부모를 y의 부모로 연결
if (x->parent== t->nil) {
t->root = y; // x가 루트 노드였다면, rb tree의 루트노드를 y로
}
else if (x==x->parent->right) {
x->parent->right = y;
}
else {
x->parent->left = y;
}
//y의 오른쪽 자식을 x로,
//x의 부모 노드를 y로, 서로 연결시켜준다.
y->right = x;
x->parent = y;

RB-isnert
//RB tree INSERT
node_t *rbtree_insert(rbtree *t, const key_t key) {
node_t *y;
node_t *x;
y = t->nil;
x = t->root;
// node_t *z;
// z: 새로 삽입하는 노드
node_t *z = (node_t*)calloc(1, sizeof(node_t));
//동적 메모리 할당-> 노드의 키 값들도 초기화 해준다.
z->key = key;
z->left = t->nil;
z->right = t->nil;
z->color = RBTREE_RED;
// 새로운 노드를 삽입할 위치 탐색
while (x != t-> nil) {
y = x;
//새로 삽입하려는 노드의 키 값이 현재 노드의 키 값보다 더 작다면 Left 이동
if ( key < x->key) {
x = x->left;
}
//새로 삽입하려는 노드의 키 값이 현재 노드의 키 값보다 더 크다면 Right 이동
else {
x = x->right;
}
}
// x 는 다음 레벨의 자식 노드를 가리키고, y는 x의 부모 노드를 가리키게 됨.
//y: 새로 삽입될 노드의 부모 노드가 됨
z->parent = y;
//부모 노드가 NIL(빈 트리)라면 루트 노드는 새로 삽입하는 노드가 된다.
if (y == t->nil) {
t->root = z;
}
// 새로 삽입하려는 노드의 키 값이 부모 노드의 키 값보다 작으면
// 새로 삽입하려는 노드는 왼쪽 자식이 된다.
else if (key < y->key) {
y->left = z;
}
// 크다면
//새로 삽입하려는 노드는 오른쪽 자식이 된다.
else {
y->right = z;
}
//새로 삽입되는 노드 z의 left, right 은 NIL노드, 색깔은 항상 RED
z->left = t-> nil;
z->right = t->nil;
z->color = RBTREE_RED; //삽입하는 노드의 색은 항상 RED로 고정한다.
//삽입할 때 레드 블랙 트리의 속성을 깨지지 않게 하기 위해 rbtree_isnert_fixup
rbtree_insert_fixup(t, z);
return t->root;
}잊지 말자..
동적 메모리 할당 후 노드의 키 값을 초기화해주어야 테스트 케이스가 통과가 된다!!


insert-fixup의 6가지 case
RB-insert-fixup
//INSERT-FIXUP
// z: 새로 삽입될 노드
void rbtree_insert_fixup(rbtree *t, node_t *z) {
node_t *y;
while (z->parent->color == RBTREE_RED) {
// 삽입하려는 노드의 부모 노드가 조부모의 왼쪽 자식일 때
if (z->parent == z->parent->parent->left){
y = z->parent->parent ->right;
// y=> 삼촌 노드! 부모의 형제 노드
// y가 red => case 1, y 가 Black => case2, 3 으로 풀이한다.
if (y->color == RBTREE_RED) {
//CASE 1:
//새로 삽입할 노드의 부모 색을 Black,
//삼촌 노드의 색을 Black,
//조부모의 색을 Red로 변경하고 조부모에서 다시 시작
z->parent->color = RBTREE_BLACK;
y->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
z = z->parent->parent;
}
else {
//CASE 2
// 새로 삽입할 노드가 오른쪽 자식이면
// 부모 노드를 기준으로 왼쪾 회전 하고 CASE 3 방식으로 해결
if (z == z->parent->right){
z = z->parent;
left_rotate(t, z);
}
//CASE 3
//새로 삽입할 노드가 왼쪽 자식이면
//부모 노드의 색을 black으로,
//조부모 노드의 색을 red로 변경하고
//오른쪽 회전하여 double red를 해결한다.
z->parent->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
right_rotate(t, z->parent->parent);
}
}
// (z-> parent == z->parent->parent->right)
// 삽입하려는 노드의 부모 노드가 조부모의 오른쪽 자식일 때
else {
//삼촌 노드 y
y = z->parent->parent->left;
//CASE 4. 삼촌 노드가 RED일 때
if (y->color == RBTREE_RED) {
z->parent->color = RBTREE_BLACK;
y->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
z = z->parent->parent;
}
else {
//CASE 5.
if (z== z->parent->left) {
z = z->parent;
right_rotate(t, z);
}
//CASE6.
z->parent->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
left_rotate(t, z->parent->parent);
}
}
}
//함수 종료 전에 루트 노드의 색깔을 Black으로 바꿔주기
t->root->color = RBTREE_BLACK;
}