rbtree_min
전체 트리에서 최솟값을 갖는 노드를 구하는 함수
node_t *rbtree_min(const rbtree *t) {
node_t *p;
p = t->root;
while(p->left != t->nil){
p = p->left;
}
return p;
}nil 노드가 나올때 까지 왼쪽 노드로 이동! 그 노드가 최솟값을 갖게 된다.
rbtree_max
node_t *rbtree_max(const rbtree *t) {
node_t *p;
p = t->root;
while(p->right != t->nil) {
p = p->right;
}
return p;
}nil노드가 나올 때까지 오른쪽 노드로 이동. 그 노드가 최댓값을 갖는 노드다.
tree_minimum, tree_maximum
-> successor, predecessor를 구하기 위한
서브 트리에서 가장 큰 값, 가장 작은 값 구하는 함수 구현
node _t *tree_maximum(rbtree *t, node_t *sub_root) {
node_t *r; // 서브트리의 루트
r = sub_root;
if (r== t->nil) {
return r;
}
while (r->right != t->nil) {
r = r->right;
}
retrun r;
} node _t *tree_minimum(rbtree *t, node_t *sub_root) {
node_t *r; // 서브트리의 루트
r = sub_root;
if (r== t->nil) {
return r;
}
while (r->left != t->nil) {
r = r->left;
}
retrun r;
} // 위의 코드와 크게 다르지 않다.
매개변수,
전체 트리의 Root에서 서브 트리의 Root로 바껴서 최솟값과 최댓값을 구하는 것만 다르다.
rb_transplant
rbtree에서 삭제할 노드 u, 대체할 노드 v
//RB Tree Transplant
// rb tree에 이식할 노드 u : 삭제할 노드 v: 대체할 노드
void rb_transplant(rbtree *t, node_t *u, node_t *v) {
//삭제할 노드 u가 루트 노드라면
//v가 루트노드를 대체해야 한다.
if (u->parent == t->nil) {
t->root = v;
}
//삭제할 노드 u가 부모 노드의 왼쪽 자식이라면
//v는 왼쪽을 대체해야 한다.
//v와 u->parent->left 연결
else if (u == u->parent->left) {
u->parent->left = v;
}
else {
//삭제할 노드가 오른쪽 자식이라면
//v는 오른쪽을 대체해야 한다. v와 u의 자리를 연결시킨다.
u->parent->right = v;
}
//대체할 노드의 Parent => 삭제한 노드의 parent 연결
v ->parent = u->parent ;
}
v의 부모 포인터를 u의 부모로 설정하여 노드 연결 관계를 업데이트
rbtree_erase
int rbtree_erase(rbtree *t, node_t *z) {
node_t *x;
node_t *y;
//z = 삭제하려는 노드가 1개 이하의 자식을 갖는 경우
y = z;
color_t y_original_color;
y_original_color = y->color;
//오른쪽 자식만 있을 때
if (z->left == t->nil){
x = z->right;
rb_transplant(t, z, z->right);
}
//왼쪽 자식만 있을 때
else if (z->right == t->nil){
x = z->left;
rb_transplant(t, z, z->left);
}
//z: 삭제하려는 노드가 2개 이상의 자식을 갖고 있을 때
// z의 Successor가 삭제된 자리를 대체한다.
else {
y = tree_minimum(t, z->right);
y_original_color = y->color;
x = y->right;
if (y->parent == z){
x->parent = y;
}
else {
rb_transplant(t, y, y->right);
y->right = z->right;
y->right->parent = y;
}
rb_transplant(t, z, y);
y->left = z->left;
y->left->parent = y;
y->color = z->color;
}
if (y_original_color == RBTREE_BLACK){
rbtree_delete_fixup(t,x);
}
return 0;
}z <- y <- x
z: rbtree에서 삭제하려는 노드
y: rbtree에서 색을 잃는 노드
-> 자식이 1개 이하면 그냥 z가 삭제,
-> 2개 이상의 자식을 가지면 z의 Successor가 원래의 색을 잃게 된다. successor가 원래 색을 잃고 z자리로 이동하게 됨
x: y의 원래 위치로 이동하는 노드
- z가 하나 이하의 child를 가질 때
: x = z의 유일한 child가 됨
- z(삭제하려는 노드)가 2개 이상의 child를 가질 때
x는 y의 자식으로 doubly black or red-and-black이 생길 수 있는 Extra-black이 붙게 되는 노드
x => y를 트리에서 제거하고 y의 위치에 올라갈 노드를 가리키는 변수
delete 함수 코드에서 잘 이해가 안간 부분
//y가 삭제될 노드 z의 자식이면 (간선 1개이면) //대체 노드 x의 부모 링크를 //y로 변경하여 트리의 구조 유지 //x가 Nil인 경우 parent를 선언해줘야 하니까 //x->parent = y를 해준다. if (y->parent == z) { x->parent =y; } else { //자식이 아니라면 //y의 위치에 y->right 이동 rb_transplant(t, y, y->right); y->right = z->right; y->right->parent = y; } //z의 위치에 y이동 rb_transplant(t, z, y); y->left = z->left; y->left->paretn = y; y->color = z->color;
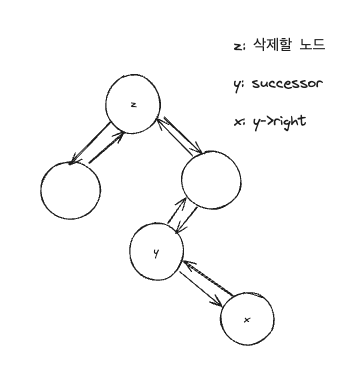




y는 루트 노드로 이동하게 되고 z는 기존의 자식들을 가리키고만 있는 상태
y와 또 원래 z의 왼쪽 서브트리를 연결하고 z의 색을 바꿔주면
결론) z 자리에 y가 오게 되고, 기존의 y의 자리에는 x로 대체됨
free(z)하면 z가 삭제돼서 사라지게 됨.
⇒ 삭제되는 색 y의 기존의 색에 따라 이후 fixup 진행하면 됨!!!
rbtree_delete_fixup
doubly black 이 생기는 4가지 case를 코드로 구현
case 1

case 2

case 3

case 4
void rbtree_delete_fixup(rbtree *t, node_t *x) {
while (x! = t->root && x->root == RBTREE_BLACK) {
//왼쪽에 doubly black이 생긴 상황
if (x == x->parent->left) {
node_t *uncle = x->parent->right;
//CASE 1 : doubly node 형제노드(삼촌)이 Red
if (uncle->color == RBTREE_RED) {
uncle->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
left_rotate(t, x->parent);
uncle = x->parent->right;
}
}
//CASE2
//삼촌의 자식 노드가 둘 다 검은색
if (uncle->left->color == RBTREE_BLACK && uncle->right->color == RBTREE_BLACK) {
uncle->color = RBTREE_RED;
x = x->parent;
}
else {
//CASE 3. 삼촌의 오른쪽 자식이 black, 삼촌의 왼쪽 자식이 Red
if (uncle->right->color == RBTREE_BLACK) {
uncle-> color = RBTREE_RED;
right_rotate(t, uncle);
uncle = x->parent->right;
}
//CASE 4. 삼촌의 오른쪽 자식의 색이 Red, 왼쪽 자식의 색이 Black
uncle->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
uncle->right->color = RBTREE_BLACK;
left_rotate(t, x->parent);
x = t->root;
}
}
//대칭된 경우
//Doubly black이 오른쪽에 있는 경우
else {
node_t *uncle = x->parent->left;
//CASE1
if (uncle->color == RBTREE_RED) {
uncle->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
right_rotate(t, x->parent);
uncle = x->parent->left;
}
//CASE 2
//삼촌의 두 자식이 모두 black
if (uncle->left->color == RBTREE_BLACK && uncle->right->color == RBTREE_BLACK) {
uncle->color = RBTREE_RED;
x = x->parent;
}
else {
//CASE 3
// 삼촌의 왼쪽 자식이 black이고 오른쪽 자식이 red
if (uncle->left->color == RBTREE_BLACK) {
uncle->right->color ==RBTREE_BLACK;
uncle->color = RBTREE_RED;
left_rotate(t, uncle);
uncle = x->parent->left;
}
//CASE 4
//삼촌의 왼쪽자식이 red
uncle->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
uncle->left->color = RBTREE_BLACK;
right_rotate(t, x->parent);
x = t->root;
}
}
}
x -> color = RBTREE_BLACK;
}rbtree_to_array
void inorder(const rbtree *t, node_t *node, key_t *arr, int *i, size_t n){
//현재 노드가 t->nil이면
if (node == t->nil) {
return ;
}
//왼쪽 서브트리 순회
inorder(t, node ->left, arr, i, n);
if (*i < n){
arr[(*i)++] = node ->key;
}
//오른쪽 서브트리 순회
inorder(t, node->right, arr, i, n );
//업데이트 된 인덱스 반환
}
//RBTREE to ARRAY
int rbtree_to_array(const rbtree *t, key_t *arr, const size_t n) {
// TODO: implement to_array
if (t->root == t->nil) {
return -1 ;
}
//배열의 인덱스 관리
int idx = 0;
//루트노드부터 중위 순회
inorder(t, t->root, arr, &idx, n );
return 0;
}

