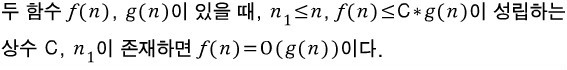정글 6일차

오늘 배운 것들

1. 시간 복잡도

1-1. 빅오 표기법

시간복잡도를 이야기하기 전 점근 표기법으로서의 빅오 표기법을 다루는 것이 좋을 것 같다.
점근 표기법은 함수의 증가율이 어떤 형태를 띄는지를 표기하는 방식이다.
컴퓨터과학에서 특히 자주 사용되는 빅오 표기법은

단순하게는

일정한 n(n1) 이상에서 g(n)보다 증가율이 높아지지 않는 함수는 O(g(n))에 속한다

고 말할 수 있을 것 같다.
즉 증가율의 상한을 나타낸다.

(n0가 매우 큰 함수의 경우에는 빅오 표기법에 의한 비교가 의미 없을 수도 있다.)

1-2. 시간 복잡도

시간 복잡도는 입력데이터의 크기(n)과 수행 시간이 어떤 형태로 비례하는지 나타내는 척도이다.
즉 n의 증가형태가 선형적인지, 로그함수적인지, 지수적인지를 알려면 시간 복잡도를 계산하면 된다.
이런 시간복잡도는 주로 빅오 표기법을 사용해 나타낸다.

예를 들면

# 양수 배열을 받아 최댓값을 반환하는 함수
def find_biggest(numbers):
	biggest = 0
	for num in numbers:
    	if num > biggest:
        	biggest = num
    return biggest

위와 같은 함수는 배열을 순회하며 비교문을 n(len(numbers))번 실행한다.
만약 오름차순으로 정렬되어 있다면 매번 조건문 안의 대입문도 실행할 것이다.
따라서 연산 횟수는 3n+1로 추산할 수 있다.(정확한 계산인지는 모르겠다.)

f(n) = 3n+1
g(n) = n 라고 하면
n1 = 1
C = 4 일 때
f(n) <= C*g(n) (n>=n1)

따라서 3n+1은 O(n)에 속한다.

2. 정렬알고리즘

정렬 알고리즘들을 공부하고 버블 정렬과 퀵 정렬을 구현해 보았다.

2-1. 수 정렬하기(백준 2750)

밀도가 낮은 물질이 떠오르는 모습이 연상되는 이름처럼 작은 수가 앞으로 점점 이동하는 정렬이다. 큰 수를 뒤로 이동하는 방식 역시 가능하다.

N = int(input())
numbers = [int(input()) for _ in range(N)]

def bubble_sort_plus(numbers :list[int], start :int) -> None:
    if start >= N-1:
        return
    
    indicator = 0
    for i in range(N-1, start, -1):
        indicator += 1
        if numbers[i-1] > numbers[i]:
            temp = numbers[i]
            numbers[i] = numbers[i-1]
            numbers[i-1] = temp
            indicator = 0
    
    if indicator == N-start-1:
        return
    bubble_sort_plus(numbers, start+1+indicator)

bubble_sort_plus(numbers, 0)
for i in numbers:
    print(i)

정렬이 완료된 부분은 다시 정렬하지 않도록 하였다.
재귀호출 직전 연속으로 교환을 수행하지 않은 횟수를 indicator에 저장하여 다음 시작 인덱스를 정할 때 사용하였다.

2-2. 수 정렬하기 2(백준 2751번)

퀵 정렬을 구현하였다.
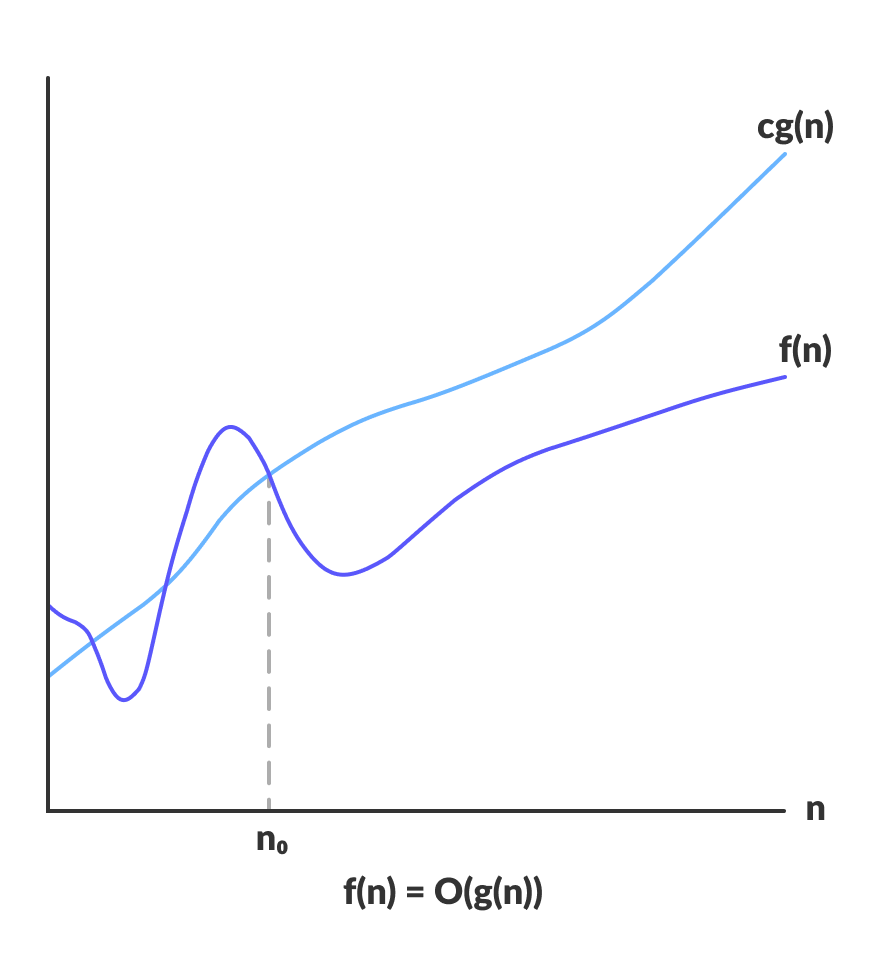
분할-정복 알고리즘의 일종으로 배열을 둘로 나눠 왼쪽은 피봇보다 작은 수, 오른쪽은 피봇보다 큰 수가 오도록 정렬하는 과정을 반복한다.

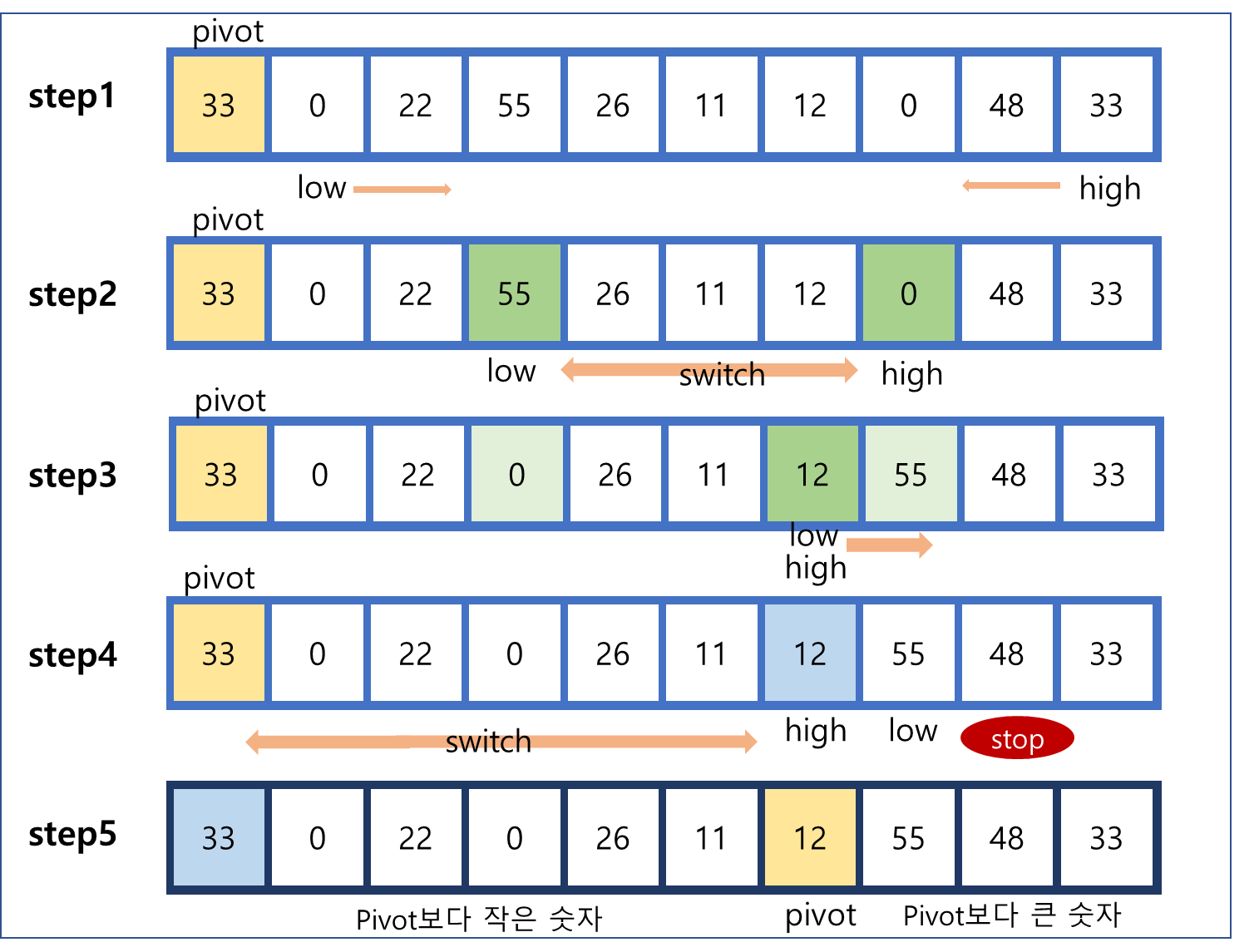
시간복잡도는 단계마다 모든 수들을 피봇과 비교하므로 비교계산 n
그리고 단계의 수는,
일단 배열을 계속 반으로 나누기 때문에 단계마다 배열 원소의 수가 반으로 줄어든다.
원소의 수가 1이 될 때까지 줄이므로 평균적으로 $n/2^k = 1$(k는 단계의 수), $log (n)=k log_2 (2)=k$ 따라서 단계의 수는 $log(n)$이다.
그러나 피봇을 계속 끝 값으로 선택하는 경우에는 비대칭으로 단계가 n만큼 늘어질 것이므로 최악의 경우에 $k=n$이다.
따라서 평균 시간복잡도는 $O(nlog(n))$ 최악의 경우는 $O(n^2)$이다.

피봇은 피봇 값만 정렬에 사용할 뿐 피봇 인덱스는 아무러 영향을 주지 않는다.
개념을 완벽하게 이해하지 못하고 구현을 시작하면 참사가 생긴다.
참사의 흔적이 코드에 남아있다.

import sys
sys.setrecursionlimit(100000)

N = int(input())
numbers = [int(sys.stdin.readline()) for _ in range(N)]

def arg_median(*args :int) -> int:
    temp = []
    for i in range(3):
        if args[(i+1)%3] > args[i]:
            if (i+1)%3 in temp:
                temp.remove((i+1)%3)
            else:
                temp.append((i+1)%3)
        else:
            if i in temp:
                temp.remove(i)
            else:
                temp.append(i)
    return temp[0]

def quick_sort(
    numbers: list[int], 
    start :int, 
    end :int) -> None:
    if start == end:
        return
    idx_l = start
    idx_r = end
    pivot = (start+end)//2
    # 피봇 선택
    pivot_cand = {0: idx_l, 1: pivot, 2: idx_r}
    med = arg_median(numbers[idx_l], numbers[pivot], numbers[idx_r])
    pivot = pivot_cand[med]
    
    n_pivot = numbers[pivot]
    while idx_l <= idx_r:
        while numbers[idx_l] < n_pivot:
            idx_l += 1
        while n_pivot < numbers[idx_r]:
            idx_r -= 1
        if idx_l > idx_r:
            break
        numbers[idx_l], numbers[idx_r] = numbers[idx_r], numbers[idx_l]
        idx_r -= 1
        idx_l += 1
        
    if idx_l < end:
        quick_sort(numbers, idx_l, end)
    if idx_r > start:
        quick_sort(numbers, start, idx_r)


quick_sort(numbers, 0, N-1)
for i in numbers:
    print(i)

처음, 끝, 중간 중 중앙값을 갖는 수를 피봇으로 선택하도록 하였다.