오늘 배운 것들
1. 완전탐색 알고리즘
완전탐색(Exhaustive Search)은 말 그대로 모든 경우의 수를 시도하는 알고리즘이다.
해당되는 방법으론:
- 모든 순열을 테스트 해보는 방법(순서를 알아야 하는 문제일 때)
- 비트마스크를 이용(flag를 써야할 때. 파이썬에선 쓰기 귀찮아 보인다.)
- DFS, BFS(그래프로 나타낼 수 있는 데이터일 때)
등 이 있다.
말만 들어도 비효율적이기 때문에
1. 완전탐색을 적용해야만 하거나
2. 완전탐색을 이용해도 될 만큼 데이터의 수가 적은 상황
에서만 이용해야 한다.
추가로 백트래킹, 다이나믹 프로그래밍, 기타 데이터의 예상 형식에 맞춘 조건 분기 등을 용해 속도를 개선한다.
1-1. 외판원 순회 2(백준 10971)
도시들의 개수와, 도시 간 이동 비용(최대 1,000,000)이 배열로 주어진다.
모든 도시를 가장 적은 비용으로 순회하는 방법을 찾아야 하는 문제이다.
import sys
N = int(sys.stdin.readline())
MIN = 1000000 * (N+1) + 1
cost_table = [[int(i) for i in sys.stdin.readline().split()] for _ in range(N)]
# O(n!)
def TSP(now :int, to_visit_list :list, cost_now :int) -> None:
global MIN
# 방문 후 기준으로 총 비용을 반환
def _visit(to :int) -> int:
cost_to = cost_table[now][to]
if cost_to:
return cost_now + cost_to
else:
return 0
# 정지조건, 더 이상 갈 곳이 남아있지 않을 때
if not to_visit_list:
# 출발지(0)로 돌아갈 수 있으면 최종 비용을 계산한다.
if cost_table[now][0]!= 0:
cost = _visit(0)
MIN = min(cost, MIN)
# 갈 곳이 남아있다면 방문한다.
for to_visit in to_visit_list:
cost = _visit(to_visit)
if cost and cost < MIN:
new_to_visit_list = to_visit_list[:]
new_to_visit_list.remove(to_visit)
TSP(to_visit, new_to_visit_list, cost)
TSP(0, list(range(1, N)), 0)
print(MIN)단순한 DFS 알고리즘이다.
출발지로 부터 계속 갈 수 있는 곳을 방문한다.
순회를 마치면 비용을 기록한다.
시간 복잡도는 O(n!)이지만 문제의 조건이 2<=n<=10이기 때문에 무리없이 풀 수 있다.
to_visit_list를 비트마스크처럼 bool자료형을 가진 리스트로 풀 수도 있지만(1000ms) 매 분기마다 모든 도시들을 순회하며 확인해야 하므로 시간이 엄청 오래걸린다.(n^n번)
그냥 방문할 목록(또는 방문한 목록)을 저장해 순회(n!번)하도록 하자(100ms).
2. 이진탐색
2-1. 나무 자르기(백준 1920)
import sys
N, M = [int(i) for i in sys.stdin.readline().split()]
TREE = [int(i) for i in sys.stdin.readline().split()]
TREE.sort()
TREE_REV = TREE[::-1]
def main():
def _cut_tree(height :int, from_top :bool) -> int:
result = 0
for i in TREE_REV if from_top else TREE:
if i > height:
result += i-height
elif i <= height:
if from_top:
break
else:
continue
return result
def _bin_search(target :int, start :int, end :int):
nonlocal max_height
if end < start:
return
else:
middle = (start + end)//2
result_mid = _cut_tree(middle, middle>N//2)
if result_mid == target:
max_height = max(max_height, middle)
elif target < result_mid:
max_height = max(max_height, middle)
_bin_search(target, middle+1, end)
else:
_bin_search(target, start, middle-1)
max_height = 0
_bin_search(M, 0, TREE[-1])
print(max_height)
main()그냥 평범한 이진탐색이다.
필요한 만큼 자를 수 있으면 더 올릴 수 있는지 이진탐색,
자를 수 없으면 어디까지 낮춰야 하는지 이진탐색.
완전탐색보다 시간복잡도 -> 로 감소했다.
2-2. 사냥꾼(백준 8983)
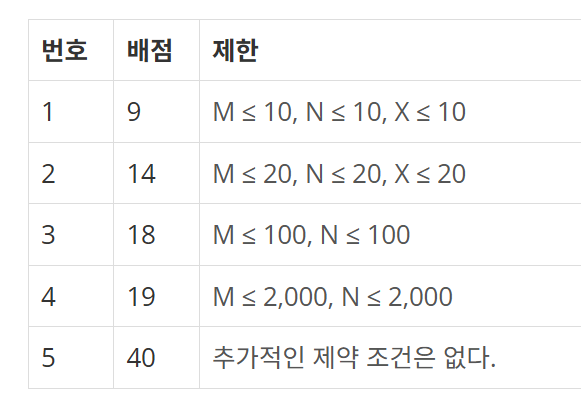100점을 맞기 위해서는 서브태스크 마지막 (0 <= N, M, L <= 1,000,000,000)을 만족해야 한다.
따라서 시간 복잡도가 높은 알고리즘으로는 100점을 맞을 수 없다.
처음에는 서브태스크를 신경쓰지 않았기 때문에 내 알고리즘이 최악의 경우 O(nm)임에도 그대로 풀었고, 역시나 마지막 서브태스크는 통과하지 못 했다.
그래도 아쉬우므로 소개하자면:
import sys
def main():
M, N, L = [int(i) for i in sys.stdin.readline().split()]
LANE = [int(i) for i in sys.stdin.readline().split()]
ANIMALS = [tuple(map(int, sys.stdin.readline().split())) for i in range(N)]
MIN_X, MAX_X = [max(0, min(LANE)-L), min(1_000_000_000, max(LANE)+L)]
MAX_Y = L
# (x, y)좌표로 표현된 동물들의 위치를, (x-y, x+y)형식으로 변환
ANIMALS = [(animal[0]-animal[1], animal[0]+animal[1]) for animal in ANIMALS if all((animal[1]<=MAX_Y, MIN_X<=animal[0]<=MAX_X))]
LANE.sort()
ANIMALS.sort()
answer = 0
# 사대 별로 돌아가며 동물들이 사정거리에 들어왔는지 체크
for h in LANE:
lb, rb = h-L, h+L
checked = []
for i, a in enumerate(ANIMALS):
if lb <= a[0]:
if a[1] <= rb:
answer += 1
checked.append(i)
elif rb < a[0]:
break
else:
checked.append(i)
for c in sorted(checked, reverse=True):
ANIMALS.pop(c)
print(answer)
main()아이디어를 잠깐 설명하자면
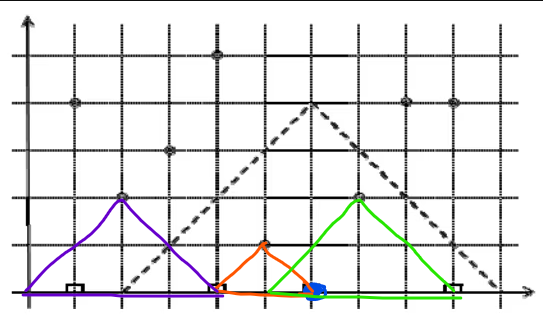
그림의 파란 사대(6)를 기준으로 판단을 하는 경우,
동물들의 위치에서 양 대각선 방향으로 선을 그어 x=0을 변으로 하는 삼각형을 그린다.
아래 변(편의상 '거리막대'라고 하겠다)이 사대를 기준으로 +-사정거리 내에 모두 들어오면 사격이 가능한 경우이다.
연산량은 그냥 맨해튼 거리를 계산하는 경우와 같지만 이렇게 하면 동물들을 정렬하여 사대별로 정지조건을 정하기 편해진다.
전제조건:
1. 사대(LANE)는 오름차순으로 정렬되어 있다.
2. 동물들은 x-y(a[0]), x+y(a[1]) (거리막대)를 키로 하여 오름차순 정렬되어 있다.
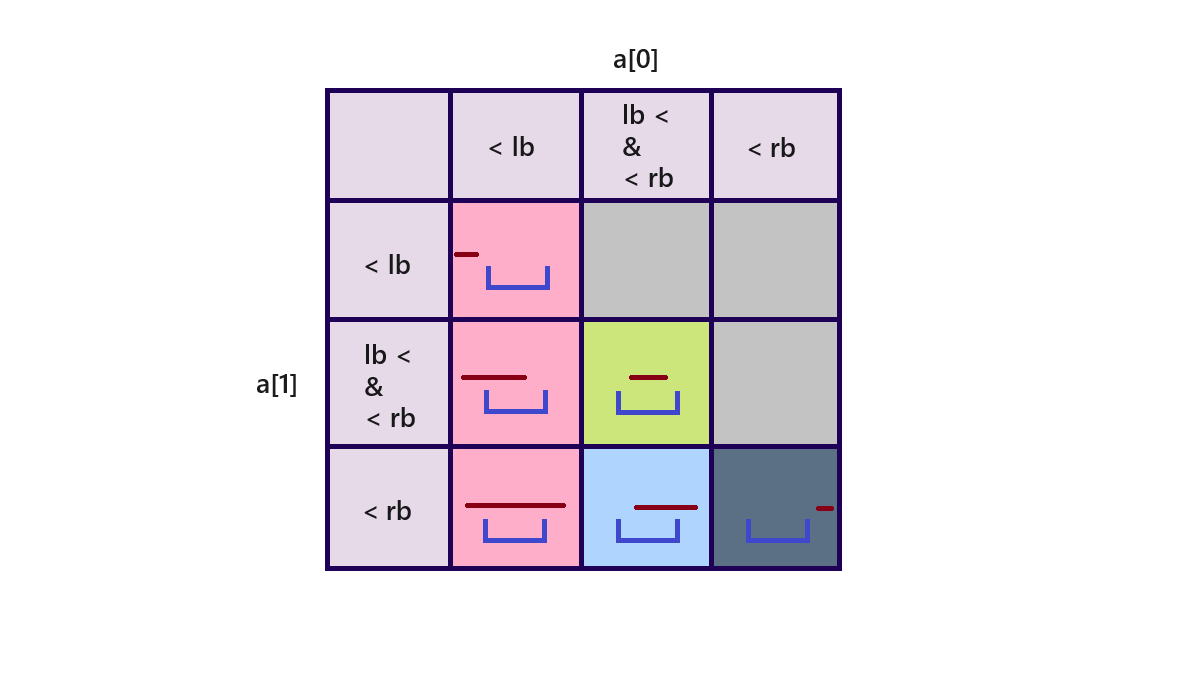특정 사대에서 동물들을 오름차순으로 순회하면서 사정거리 내에 들어오는지를 체크할 때의 경우의 수를 표현한 그림이다.
파란색 위가 잘린 네모는 사대의 왼쪽경계(lb), 오른쪽경계(rb)의 범위를 나타내고
- 붉은 선은 동물들의 거리막대(a[0], a[1])를 선분으로 표시했다.
- 분홍 칸은 더 탐색할 필요가 없는 경우를 나타낸다.
사대가 오름차순 정렬 되어있기 때문에 이후의 사대에서도 사정거리를 벗어날 것이기 때문이다. - 연두 칸은 사정거리 내에 들어온 경우이다. 정답 숫자에 1을 추가하면 된다.
- 파란 칸은 사정거리 내에 들어오지는 않았지만 이후에 다시 확인할 필요가 있는 경우이다.
특히 짙은 파란 칸은 이번 사대에서는 더 이상 탐색할 필요가 없는 경우이다.
위와 같은 기준으로 동물들을 판단해 나갔다.
하지만 시간복잡도가 이기 때문인지, N, M이 큰 경우에는 시간초과가 떴다.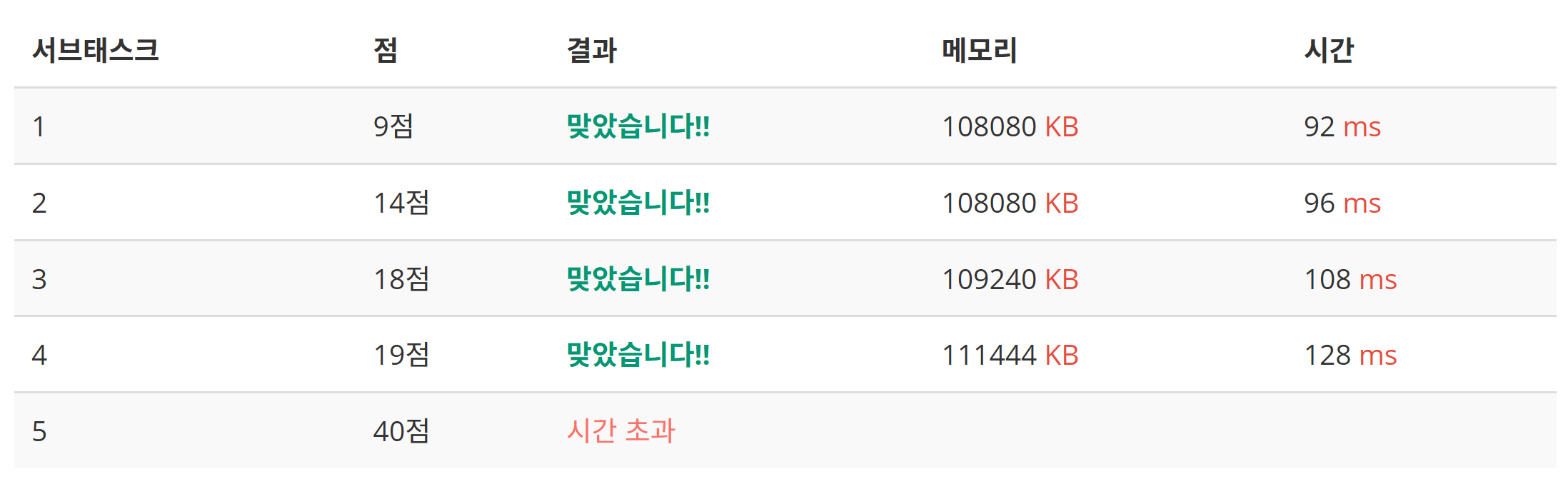
이진탐색을 써야한다는 힌트를 얻어 알고리즘을 수정했다.
힌트를 받고도 오랫동안 고민했으므로 아마 힌트가 없었으면 못 풀었지 싶다.
import sys
from collections import defaultdict
def main():
def bin_search(l, r, start, end):
if start >= end:
return False
mid = (end+start)//2
if LANE[mid] < l:
return bin_search(l, r, mid+1, end)
elif r < LANE[mid]:
return bin_search(l, r, start, mid)
else:
return True
M, N, L = [int(i) for i in sys.stdin.readline().split()]
LANE = [int(i) for i in sys.stdin.readline().split()]
ANIMALS = [tuple(map(int, sys.stdin.readline().split())) for i in range(N)]
MIN_X, MAX_X = [max(0, min(LANE)-L), min(1_000_000_000, max(LANE)+L)]
MAX_Y = L
animals = defaultdict(list)
for x, y in ANIMALS:
if all((y<=MAX_Y, MIN_X<=x<=MAX_X)):
animals[y].append(x)
LANE.sort()
answer = 0
for y, xs in animals.items():
for x in xs:
if bin_search(x-(L-y), x+(L-y), 0, M):
answer += 1
print(answer)
main()y값이 같은 동물들을 묶은 뒤 동물들을 순회하며 사정거리에 들어오는 사대가 있는지를 이진탐색하는 방식이다.
사대를 이진탐색하므로 시간복잡도는
풀고나니 아주 간단하지만 언제나 아이디어를 떠올리는 것이 가장 어려운 것 같다.
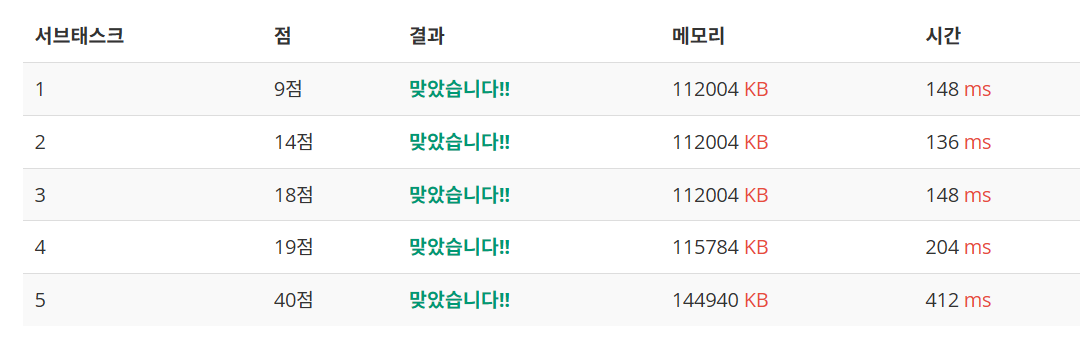그러나 처음 풀었던 것에 비해서 서브태스크 1~4에서는 더 느리다.
빅오표기법 상으로 더 나은 시간복잡도를 가지지만 느린 경우가 생기는 이유는 빅오표기법의 정의를 생각한다면 알 수 있다.
3. 소소한 것들
3-1. 파이썬 디버깅
vscode에서 디버깅을 눌러도 아무 동작을 안해서
그동안 눈으로 디버깅 해왔는데 드디어 방법을 알았다.
launch.json을 생성해야 작동하는 것이었다.
이모티콘가지고 난리 부렸을 때 알고 있었으면 시간이 절반으로 줄었을 지도(진심으로)
Step Over: 현재 라인을 실행 후 다음 라인으로 이동(함수를 호출해도 다 실행해버린다. 실행만 시키고 싶을 때)
Step Into: 현재 라인을 실행(함수를 호출하면 함수 안으로 이동하여 보여준다. 함수 내부의 동작도 보아야 할 때)
Step Out: 함수를 다 실행하고 밖으로 이동(함수에서 볼 일 다 봤을 때)
