오늘 배운 것들

1. 최단거리 알고리즘 보충

출처
가중치가 없거나 0, 1만으로 이루어진 경우에는 BFS를 사용하는 것이 효율적이다.
그렇지 않은 경우에 최단거리를 구하는 알고리즘들을 정리

1-1. 다익스트라

1. 시작 정점 결정 0으로 초기화 후 우선순위 큐에 담음
2. 나머지 정점 무한대로 초기화
3. 우선순위 큐에서 pop한 후 그 정점에서 갈 수 있는 정점를 확인
4. 더 빠르다면 갱신하고 우선순위 큐에 넣는다.
5. 방문했거나, 더 느리다면 continue
6. 우선순위 큐가 빌 때까지 3-5번을 반복한다.

• 시간 복잡도는 $O(E+VlogV)$
• 하나의 정점에서 모든 정점으로 가는 최단거리를 구함.
• 우선순위 큐 사용
• 가중치는 모두 양수

1-2. 플로이드 워셜

1. 가중치를 반영한 인접행렬을 만들고, 다른 정점을 거쳐가야 하는 정점은 무한대로 초기화
2. 반복문으로 경유지를 돌아가며 지정
3. 경유지를 기준으로, 해당 경유지를 거쳐가는게 빠르다면 갱신
   (i 가 경유지라면, A[j][k] = min(A[j][k],A[j][i]+A[i][k]) )
4. 모든 정점을 경유지로 선정해가며 3번 반복

• 시간 복잡도는 $O(V^3)$
• 경유지를 기준으로 돌아가며 모든 정점들을 탐색하므로 반복문의 최상단은 경유지 순회여야 한다.
• 모든 정점에서 모든 정점으로 가는 최단거리를 구함.
• 가중치가 음수인 경우도 적용 가능
• 일관된 시간복잡도를 갖는 것은 다익스트라 대비 장점
• 그러나 음수 가중치가 아니라면 시간복잡도상 다익스트라가 유리한 경우가 많다.

1-3. 벨만포드

1. 시작 정점 0으로 초기화
2. 나머지 정점 무한대로 초기화
3. 나머지 정점 방문하며 주변 정점에 방문하는 최단거리 갱신 ($V-1$ 번 반복)
4. 한 번 더 방문하면 업데이트 되는지 확인 (사이클 확인, 사이클이 있다면 false)

• 시간 복잡도는 $O(V*E) ~= O(V^3)$ (보통 $V^2>E$)
• 하나의 정점에서 모든 정점으로 가는 최단거리를 구함.
• 가중치가 음수인 경우도 적용 가능
• 가중치가 사이클을 이루는 경우 사용 불가능
• 가중치가 음수가 아니라면 다익스트라가 유리

2. 위상정렬

방향 그래프를 방향을 거스르지 않는 순서로 정렬하는(순회하는) 알고리즘이다.
보통 떠오르는 정렬 알고리즘과 다르게 한 가지 경우로 유일하게 결정되지 않는다.
순서를 가져야 하므로 사이클이 없어야 한다.

정렬 후에도 그래프가 유지되어있다.
위상정렬은 그래프를 변경하는 알고리즘은 아니다.

2-1. Kahn 알고리즘

1. 진입차수(자신을 향하는 간선의 수)가 0인 정점을 큐에 넣는다.
2. 큐에서 하나씩 정점을 뽑아 출력(작업 수행)한다.
3. 출력(작업)이 끝난 정점이 가리키는 간선들을 제거한다.(가리키던 정점의 진입차수가 하나 씩 준다.)
4. 큐가 빌 때까지 2로 돌아간다.
5. 비연결 그래프의 경우 다시 1로 돌아간다.

2-2. DFS를 이용

1. DFS로 정점을 탐색하다 진출차수가 0인 노드를 발견하면 스택에 넣고 제거한다.
2. 그래프가 빌 때까지 반복한다.
3. 스택을 모두 출력하면 위상정렬된 순서

2-3. 활용

• 작업 스케줄링, 종속성 처리
• 부분정렬: 데이터의 비교가 일부만 수행된 경우에 조건을 만족하는 순서 찾기(예: 주어진 물체의 대소비교 정보로는 크기 순으로 나열할 수 없을 때)
• 사이클 감지, 심볼 추적

2-4. 줄 세우기(백준 2252)

import sys
from collections import deque

input = sys.stdin.readline

def main() -> None:
    N, M = map(int, input().split())
    inbound = {i: 0 for i in range(1, N+1)}
    outbound = {i: [] for i in range(1, N+1)}
    q = deque()
    for _ in range(M):
        frm, to = map(int, input().split())
        # if to not in outbound[frm]:
        outbound[frm].append(to)
        inbound[to] += 1
    
    for i in inbound.items():
        q.append(i[0]) if i[1] == 0 else None
    result = []
    while q:
        i = q.popleft()
        result.append(i)
        for j in outbound[i]:
            inbound[j] -= 1
            if inbound[j] == 0:
                q.append(j)
    print(*result)
    
if __name__ == "__main__":
    main()

위상정렬의 기본

2-5. 장난감 조립(백준 2637)

import sys
from collections import deque

input = sys.stdin.readline

class Vertex:
    def __init__(self, key: int) -> None:
        self.key = key
        self.inbound: list[tuple[int, int]] = [] # (키, 가중치)
        self.outbound: int = 0
        self.quantity: int = 0

def main() -> None:
    N = int(input())
    M = int(input())
    vertexes: dict[int, Vertex] = {}
    q = deque()
    # 데이터 불러오기
    for _ in range(M):
        to, frm, quantity = map(int, input().split())
        if frm not in vertexes:
            vertexes[frm] = Vertex(frm)
        if to not in vertexes:
            vertexes[to] = Vertex(to)
        vertexes[frm].outbound += 1
        vertexes[to].inbound.append((frm, quantity))
    
    # 최초 큐 삽입
    vertexes[N].quantity = 1
    q.append(N)
    while q:
        curr = q.popleft()
        for key, weight in vertexes[curr].inbound:
            vertexes[key].quantity += vertexes[curr].quantity * weight
            vertexes[key].outbound -= 1
            if vertexes[key].inbound and vertexes[key].outbound <= 0:
                q.append(key)
        del vertexes[curr]
        
    for v in sorted(vertexes):
        print(vertexes[v].key, vertexes[v].quantity)
    
if __name__ == "__main__":
    main()

줄 세우기와 같으나 진출차수를 기준으로 위상정렬을 하는 것만 다르다.

2-6. 그래프 수정(백준 1432)

import sys

input = sys.stdin.readline

class Vertex:
    def __init__(self, key: int) -> None:
        self.key: int = key
        self.adj_vector: list = []

def main() -> None:
    def find_no_outbound(include: list) -> list:
        for i in include:
            if all(not vertexes[i].adj_vector[j-1] for j in include):
                include.remove(i)
                return i
        return None
    # 데이터 불러오기
    N = int(input())
    vertexes: dict[int, Vertex] = {i: Vertex(i) for i in range(N, 0, -1)}
    for i in range(1, N+1):
        vertexes[i].adj_vector = list(map(int, list(input().rstrip())))
    
    q = list(vertexes.keys())
    n = N
    while q:
        next = find_no_outbound(q)
        if next is None:
            print(-1)
            return
        vertexes[next].key = n
        n -= 1
    print(*[vertexes[i].key for i in range(1, N+1)])
    
if __name__ == "__main__":
    main()

조건이 헷갈렸던 문제

답이 여러 개일 경우에는 사전 순으로 제일 앞서는 것을 출력한다.

이 조건은 포함관계의 두 가지 요구를 함축하고 있다.

1. 같은 정점을 가리키는 정점은 원래 번호 순으로 번호를 부여할 것
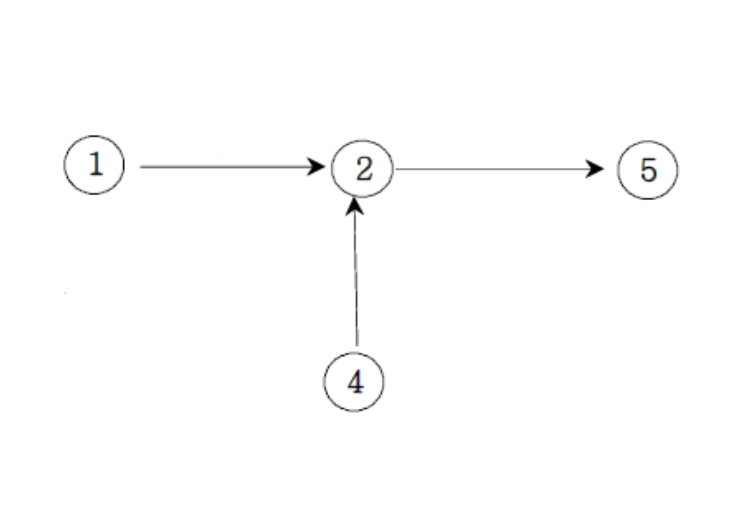   1, 4 중 1에 번호를 먼저 부여해야 한다.

   기존 번호	1	2	4	5
   새 번호	1	3	2	4

2. 같은 정점을 가리키는 경로는 가장 작은 번호의 정점을 포함한 경로를 우선해서 번호를 부여할 것
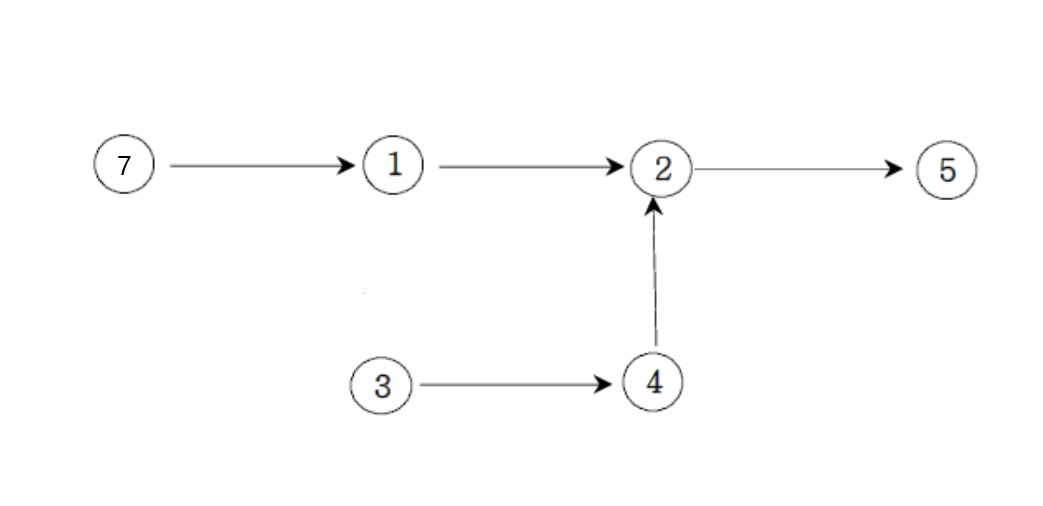   진입차수가 0인 노드 중 가장 작은 번호는 3이지만
   7-1-2경로와 3-4-2경로 중 가장 작은 번호는 1이므로 7-1-2경로에 먼저 부여해야 한다.

   기존 번호	1	2	3	4	5	7
   새 번호	2	5	3	4	6	1

1.만을 고려한다면 작은 정점 번호에 우선순위를 부여한 위상정렬로 충분하겠지만 2.까지는 만족할 수 없다.
진출차선이 0인 정점부터 탐색하는 위상정렬로 N부터 번호를 부여한다면 해결할 수 있다.

2-7. 임계경로(백준 1948)

import sys
from collections import deque

input = sys.stdin.readline

class Vertex:
    def __init__(self, key: int) -> None:
        self.key = key
        self.outbound: list[tuple[int, int]] = [] # (키, 가중치)
        self.inbound: int = 0
        self.max_sum_weight: int = 0
        self.route: set[tuple[int, int]] = set() # (출발, 도착)

def main() -> None:
    # 데이터 불러오기
    N = int(input())
    M = int(input())
    vertexes: dict[int, Vertex] = {}
    for _ in range(M):
        frm, to, weight = map(int, input().split())
        if frm not in vertexes:
            vertexes[frm] = Vertex(frm)
        if to not in vertexes:
            vertexes[to] = Vertex(to)
        vertexes[frm].outbound.append((to, weight))
        vertexes[to].inbound += 1
    START, END = map(int, input().split())
    
    # 최초 큐 삽입
    q: deque[int] = deque()
    q.append(START)
    while q:
        curr = q.popleft()
        for key, weight in vertexes[curr].outbound:
            new_weight = vertexes[curr].max_sum_weight + weight
            if vertexes[key].max_sum_weight == new_weight:
                vertexes[key].route.update(vertexes[curr].route | set([(curr, key)]))
            elif vertexes[key].max_sum_weight < new_weight:
                vertexes[key].max_sum_weight = new_weight
                vertexes[key].route = vertexes[curr].route | set([(curr, key)])
            vertexes[key].inbound -= 1
            if vertexes[key].inbound == 0:
                q.append(key)
        if curr != END:
           del vertexes[curr]
    print(vertexes[END].max_sum_weight, len(vertexes[END].route), sep="\n")
    
if __name__ == "__main__":
    main()

특이하게도 최단거리가 아닌 최장거리를 구하는 문제
다만 최장거리 경로가 복수인 경우를 포함해서, 최장거리로 이동하는데 사용한 간선의 개수 또한 출력해야한다.
나는 위상정렬로 순회하며 최장거리를 갱신할 때 이전 경로들도 같이 전달하는 방식으로 구현했다.
갱신할 때엔 경로들을 덮어쓰고, 새 가중치 합과 같을 때엔(최장거리 경로가 둘 이상) 원래의 경로에 추가해주었다.
경로를 저장하면서 메모리를 많이 사용하여 방문한 정점은 삭제하는 등 끼워맞추기로 풀어 정확한 풀이인지는 모르겠다.
개선의 여지는 많지만 내 체력은 없다.

3. B-트리

이진탐색트리가 노드별로 하나의 값을 가지며 크다/작다 두 가지로 탐색을 하였다면
M차 B-트리는 노드별로 M-1개의 값을 가지며 M 가지 자식을 탐색하는 트리이다.
2차 B-트리가 이진탐색트리와 형태가 같다.
삽입, 삭제 방식은 다른데 B-트리는 상향식으로 삽입이 일어난다.
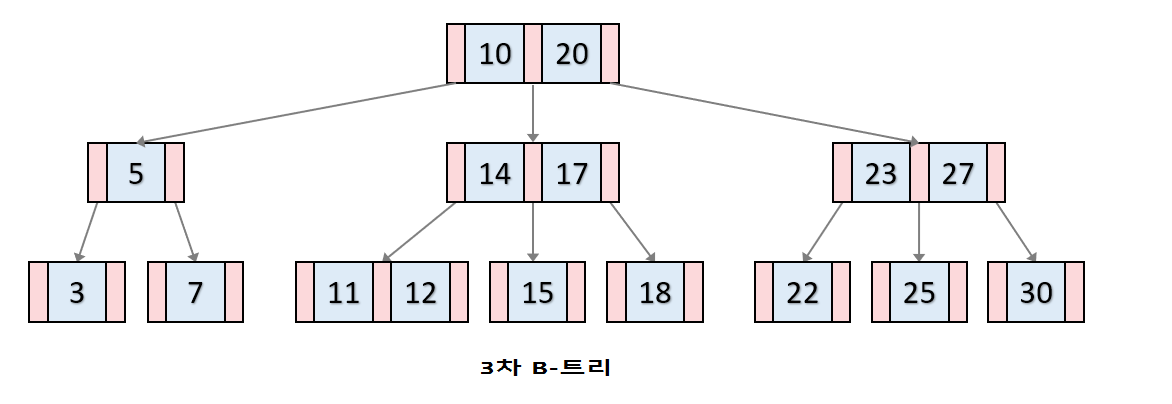참고

4. 트라이(Trie, retrieval tree)

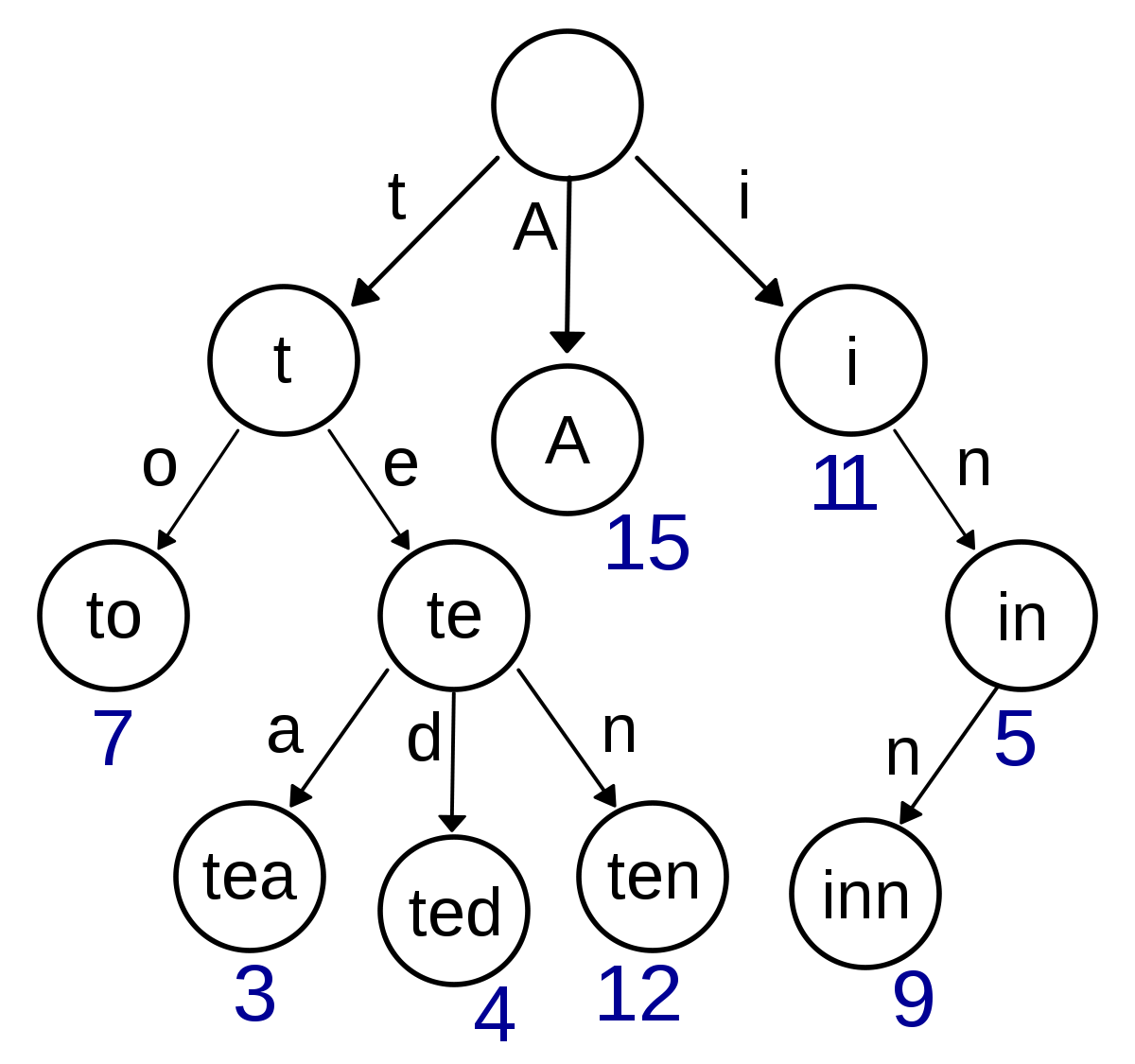문자열을 저장하고 탐색하기 위한 트리
자동완성, 검색 등에 자주 사용한다.
문자열을 탐색할 때 하나씩 비교하지 않고 트리를 내려가므로 빠르나 트리를 구성하기 위해 메모리를 많이 사용한다.

5. 기타문제

5-1. 동전 2(백준 2294)

import sys

input = sys.stdin.readline

def main() -> None:
    def check_cases(target: int, type_idx: int, n_coins: int) -> bool:
        if type_idx >= N:
            return False
        elif type_idx == N-1:
            return all((target//COIN_TYPE[type_idx] <= n_coins, target%COIN_TYPE[type_idx]==0))
        for i in range(min(target//COIN_TYPE[type_idx], n_coins), -1, -1):
            # 맞아 떨어지면
            residual = target - COIN_TYPE[type_idx] * i
            if residual == 0:
                return True
            elif COIN_TYPE[-1] <= residual <= COIN_TYPE[type_idx+1]*(n_coins-i):
                if check_cases(residual, type_idx+1, n_coins-i):
                    return True
        return False
    N, K = map(int, input().split())
    COIN_TYPE = []
    for _ in range(N):
        c = int(input())
        if c not in COIN_TYPE:
            COIN_TYPE.append(c)
    COIN_TYPE.sort(reverse=True)
    N = len(COIN_TYPE)
    for i in range(1, K//COIN_TYPE[-1]+1):
        if check_cases(K, 0, i):
            print(i)
            return
    print(-1)
    
if __name__ == "__main__":
    main()

남은 동전의 종류로는 목표 금액에 못 미칠 때,
한 종류의 동전만 남았지만 나누어 떨어지지 않을 때 불가능하다고 판단하고
큰 금액권부터 채우는 등 사람이 돈을 맞추는 모습을 모방하였다.

파이썬 기준 제일 빠르다.

5-2. 구슬 찾기(백준 2617번)

import sys
from collections import deque

input = sys.stdin.readline

class Vertex:
    def __init__(self, key: int) -> None:
        self.key = key
        self.outbound: list[int] = []
        self.inbound: list[int] = []
        self.nth_left: int = 0
        self.nth_right: int = 0

def main() -> None:
    N, M = map(int, input().split())
    vertexes: dict[int, Vertex] = {i: Vertex(i) for i in range(1, N+1)}
    for _ in range(M):
        frm, to = map(int, input().split())
        if frm == to:
            continue
        vertexes[frm].outbound.append(to)
        vertexes[to].inbound.append(frm)
    
    def dfs_right(i):
        visited[i] = 1
        # if vertexes[i].nth_right:
        #     return vertexes[i].nth_right
        level = 1
        for v in vertexes[i].outbound:
            if v not in visited:
                level += dfs_right(v)
        # vertexes[i].nth_right = level
        return level
    
    def dfs_left(i):
        visited[i] = 1
        # if vertexes[i].nth_left:
        #     return vertexes[i].nth_left
        level = 1
        for v in vertexes[i].inbound:
            if v not in visited:
                level += dfs_left(v)
        # vertexes[i].nth_left = level
        return level
    
    for i in range(1, N+1):
        visited = {}
        vertexes[i].nth_left = dfs_left(i)
        visited = {}
        vertexes[i].nth_right = dfs_right(i)
    
    mid = N // 2 +1
    result = sum((vertexes[i].nth_left > mid or vertexes[i].nth_right > mid) for i in vertexes)
    print(result)
    
if __name__ == "__main__":
    main()

순환이 없는 경우이므로 중복 방문을 체크하지 않아도 된다고 생각해서 오래 헤맸다.
순환이 없더라도 경로가 중복되는 경우는 얼마든지 있을 수 있다.
+ 주석처리된 부분을 넣으면 왜 오답이 되는지 아직도 모르겠다.