이진트리(Binary Tree)
Child노드를 최대 2개 가질 수 있는 노드로 구성된 트리 구조.
노드는 (key,value)와 (부모 노드 링크, 자식 노드 링크 2개(left,right))로 구성되어있다.
이진트리의 순회(traversal)
이진트리의 노드들을 빠짐없이 순회하여 탐색하는 방식으로, 전위/중위/후위순회가 있다.
노드 M의 왼쪽 subtree를 L, 오른쪽 subtree를 R이라고 할 때,
- 전위순회(pre-order) : M → L → R
- 중위순회(in-order) : L → M → R
- 후위순회(post-order) : L → R → M
Python 코드
class Node:
def __init__(self,key,parent=None,left=None,right=None):
self.key = key
self.parent = parent
self.left = left
self.right = right
def __str__(self):
return str(self.key)
def pre_order(self): # M -> L -> R 순서로 전위순회
if self != None:
print(self.key)
if self.left:
self.left.pre_order()
if self.right:
self.right.pre_order()
def in_order(self): # L -> M -> R 순서로 중위순회
if self != None:
if self.left:
self.left.in_order()
print(self.key)
if self.right:
self.right.in_order()
def post_order(self): # L -> R -> M 순서로 후위순회
if self != None:
if self.left:
self.left.post_order()
if self.right:
self.right.post_order()
print(self.key)
a,b,c,d,e,f,g,h,i = Node('A'),Node('B'),Node('C'),Node('D'),Node('E'),Node('F'),Node('G'),Node('H'),Node('I')
f.left, f.right = b,g
b.parent, b.left, b.right = f,a,d
a.parent = b
d.parent, d.left, d.right = b,c,e
c.parent = d
e.parent = e
g.parent, g.right = f,i
i.parent, i.left = g,h
h.parent = i
코드를 통해 위와 같은 트리 구조를 만들고,
f.pre_order()
print("")
f.in_order()
print("")
f.post_order()루트 노드가 되는 f 노드를 기준으로 순회를 시키면
pre-order : F B A D C E G I H
in-order : A B C D E F G H I
post-order : A C E D B H I G F
순서로 순회한다.
이진탐색트리(Binary Search Tree)
- 각 노드의 왼쪽 subtree의 키값 <= 노드의 키값
- 각 노드의 오른쪽 subtree의 키값 > 노드의 키값
두 성질을 만족하는 이진트리를 이진탐색트리, BST라고 한다.
연산 & 수행시간
탐색/삽입 연산 : findLoc 함수로 노드의 위치, 혹은 노드가 삽입되어야할 위치를 찾아낸다.
findLoc : 최악의 경우 root에서 가장 깊은 level까지 이동해야 하므로 O(h)
탐색과 삽입은 findLoc외에는 상수 시간 연산이 가능하므로
☆search : O(h)
insert : O(h)
삭제 연산 : 둘다 O(h)
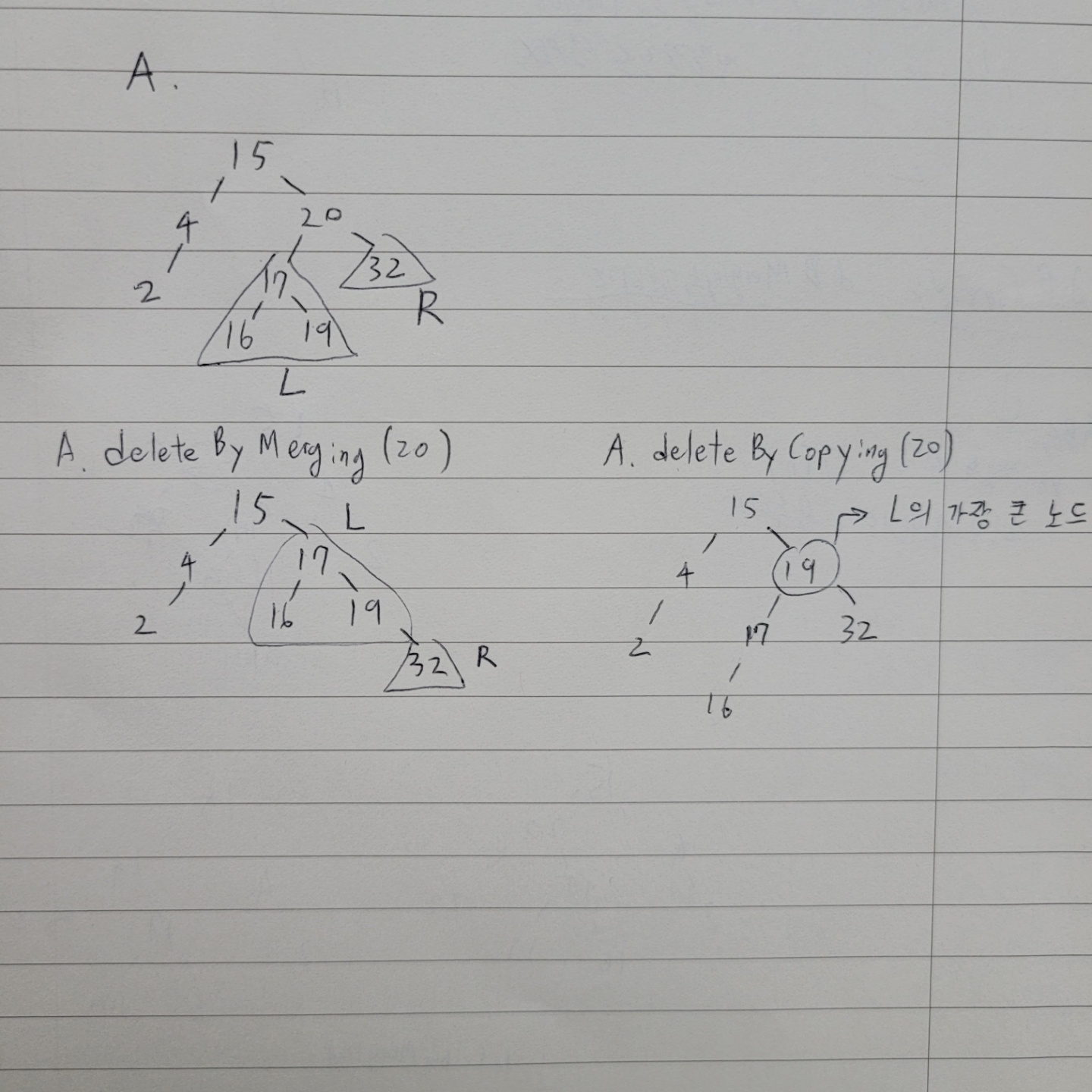
deleteByMerging : 삭제할 노드 x의 왼쪽 subtree(L)를 노드 x에 붙이고, x의 오른쪽 subtree(R)를 L의 최대한 오른쪽 child노드에 붙인다.
deleteByCopying : L에서 가장 큰 노드(m)의 키값을 x에 복사하고, m의 subtree가 m의 자리에 오도록 m의 parent의 child로 붙인다.
Python 코드
class BST: # 각 노드의 왼쪽 sub-tree의 키값 <= 노드의 키값 and 오른쪽 sub-tree의 키값 > 노드의 키값 만족하는 이진트리
def __init__(self):
self.root = None
self.size = 0
def __len__(self):
return self.size
def __iter__(self):
return self.root.__iter__()
def findLoc(self,key): # key값이 노드 v에 있으면 해당 노드 return, 없다면 노드가 삽입될 v의 parent노드 p return
if self.size == 0:
return None
p = None
v = self.root
while v != None:
if v.key == key:
return v
elif v.key < key: # v 노드의 키값이 찾으려는 키값보다 작다면 오른쪽 child노드로 이동
p = v
v = v.right
else: # v 노드의 키값이 찾으려는 키값보다 크다면 왼쪽 child노드로 이동
p = v
v = v.left
# 반복문이 끝나는 것은 leaf노드까지 내려와도 키값을 못 찾아 트리에 키값이 없는 것이므로 p 반환
return p
def search(self,key): # 탐색 연산
v = self.findLoc(key)
if v.key != key: # findLoc에서 나온 노드의 키값과 검색할 키값 비교
print(key,"is not in the tree!")
return None
else:
print(key,"is in the tree!")
return v
def insert(self,key): # 삽입 연산
p = self.findLoc(key)
v = Node(key)
if p == None or p.key != key:
if p == None: # 트리 사이즈가 0, 즉 빈 트리인 경우 삽입하는 노드는 root가 된다
self.root = v
else: # findLoc으로 찾은 위치 p에 키값이 이미 존재하는 경우가 아니라면
v.parent = p
if p.key >= key:
p.left = v
else:
p.right = v
self.size += 1
return v
else: # findLoc으로 찾은 위치 p에 키값이 이미 존재
print("Key is already in the tree!")
return p
# 노드 x의 왼쪽 subtree의 첫 노드 a의 링크를 노드 x의 위치로 가게끔 옮기고
# 노드 x의 오른쪽 subtree의 첫 노드 b를 왼쪽 subtree의 오른쪽 끝에 링크하여 붙여서 BST를 만족시키면서 노드 x를 삭제
# 고려할 case 1) a == None?(왼쪽 subtree의 존재 여부)
# 고려할 case 2) x == root?(삭제하려는 노드가 루트일 경우)
def deleteByMerging(self,x):
a, b, pt = self.findLoc(x).left, self.findLoc(x).right, self.findLoc(x).parent
# c = x 자리를 대체할 노드
# m = 왼쪽 subtree에서 가장 큰 노드
# case 1)
if a != None:
c = a
# 왼쪽 subtree의 오른쪽 끝(가장 큰) 노드를 찾아서, 노드 b의 parent로 링크
m = a
while m.right:
m = m.right
if b != None:
b.parent = m
m.right = b # b == None이더라도 m.right를 b로 지정하여 leaf노드로 만들어줌
else : # a== None, 즉 왼쪽 subtree가 없으면 b를 x 자리로 이동
c = b
# case 2)
if pt != None:
if c:
c.parent = pt
if pt.key < c.key:
pt.right = c
else:
pt.left = c
else: # 노드 x가 root인 경우 c를 root로 지정
self.root = c
if c: c.parent = None
self.size -= 1
# 노드 x의 왼쪽 subtree의 가장 큰 노드 m을 찾아 그 키 값을 노드 x에 copy
# m 은 오른쪽 child노드는 없고, 왼쪽 subtree는 존재할 수도 있으니, m 자리에 왼쪽 subtree 연결
def deleteByCopying(self,x):
x = self.findLoc(x)
a = x.left
m = a
while m.right:
m = m.right
x.key = m.key
# x의 왼쪽 child노드가 m일 경우
if m == a:
a = m.left
m.left.parent = x
else:
if m.left:
m.left.parent = m.parent
m.parent.right = m.left
self.size -= 1
A = BST()
A.insert(15)
A.insert(4)
A.insert(2)
A.insert(20)
A.insert(17)
A.insert(16)
A.insert(19)
A.insert(32)

print(A.root) # 15
print(A.root.key) # 15
A.root.pre_order() # 15 4 2 20 17 16 19 32
print(A.root.left) # 4
print(A.root.left.parent) # 15
print(A.size) # 8
A.search(9) # 9 is not in the tree!
A.search(32) # 32 is in the tree!
A.deleteByMerging(20)
A.root.pre_order() # 15 4 2 17 16 19 32만약 deleteByCopying으로 같은 노드를 삭제한다면,
A.deleteByCopying(20)
A.root.pre_order() # 15 4 2 19 17 16 32이를 트리 구조로 나타내면