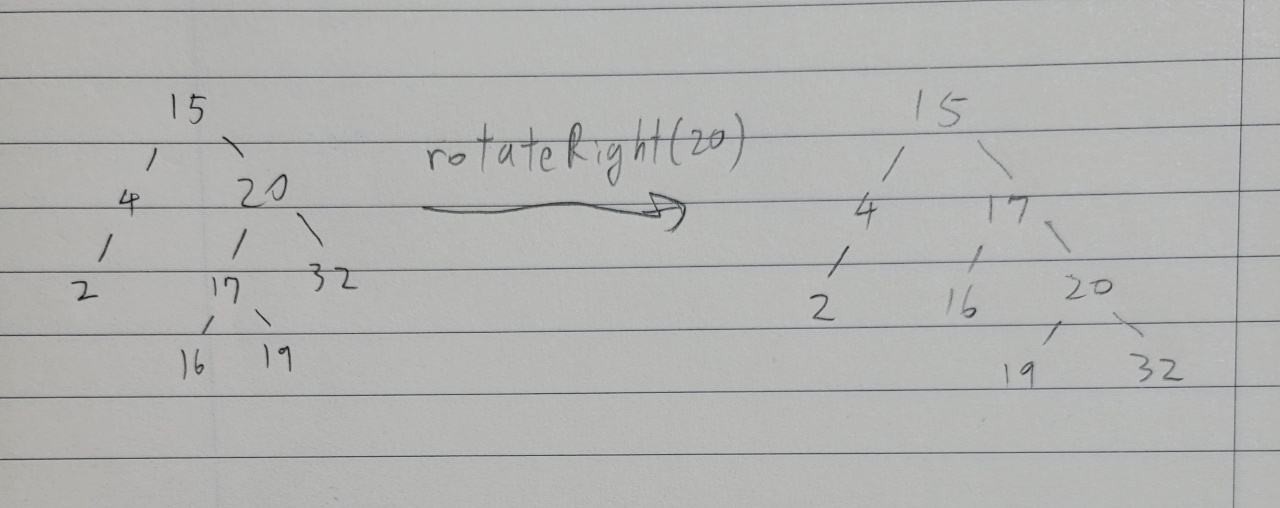균형이진탐색트리(Balanced BST)

이진탐색트리의 노드의 개수를 N, 트리의 높이를 h라고 할 때,

log(2)(N+1) - 1 <= h < N 이다.

Balanced BST는 이진탐색트리 연산의 수행시간인 O(h)를 O(logN)이 되도록 유지시키는, 즉 높이를 최소화하는 BST

균형이진트리의 예시

• AVL
• Red-Black
• (2,3,4)
• Splay....

Rotation

균형이진탐색트리는 노드의 Rotation을 통해 양쪽 subtree의 균형을 맞출 수 있다.

rotateRight(z)

1. 노드 z와 노드 z의 오른쪽 subtree를 오른쪽 방향으로 1레벨 낮춘다.
2. 노드 z의 왼쪽 child노드 x를 z의 자리로 1레벨 올린다.
3. 노드 x의 오른쪽 child노드 b를 내려간 z의 왼쪽 child로 지정한다.

위를 구현하려면 아래 그림과 같이 총 6개의 링크 수정이 필요하다.

각각의 링크 수정은 상수시간이므로, 시간 복잡도는 O(1)

rotateLeft(z)

rotateRight(z)에서 방향을 반대로 하여 구현이 가능하다.

시간 복잡도 역시 동일하게 O(1)

Python 코드

기존에 작성한 BST 클래스를 상속한 BalancedBST 클래스를 선언하였다.

class BalancedBST(BST):
    def rotateRight(self,z):
        z = self.search(z) # 트리 내에서 rotate할 z노드를 검색하여 리턴
        if not z: return # rotation 대상이 없음
        x = z.left
        if not x: return # rotation 필요 x
        b = x.right
        # 1. rotation의 대상인 z의 left child인 x를 z의 위치로 옮김(오른쪽 rotation)
        x.parent = z.parent
        if z.parent: # 올라간 x가 root가 아니었을 경우, z가 z.parent의 어느쪽 child인지 판별 후 그 위치에 링크 연결
            if z.parent.left == z:
                z.parent.left = x
            else:
                z.parent.right = x
        # 2. x의 right child로 z 지정
        x.right = z
        z.parent = x
        # 3. x의 원래 right child노드인 b를 z의 left child로 이동
        z.left = b
        if b: # b가 None이 아니라면
            b.parent = z
        # 이렇게 윗 레벨로 올라간 x 노드가 루트라면 새 루트 노드 지정
        if self.root == z:
            self.root = x

    def rotateLeft(self,z):
        z = self.search(z) # 트리 내에서 rotate할 z노드를 검색하여 리턴
        if not z: return # rotation 대상이 없음
        x = z.right
        if not x: return # rotation 필요 x
        b = x.left
        # 1. rotation의 대상인 z의 left child인 x를 z의 위치로 옮김(오른쪽 rotation)
        x.parent = z.parent
        if z.parent: # 올라간 x가 root가 아니었을 경우, z가 z.parent의 어느쪽 child인지 판별 후 그 위치에 링크 연결
            if z.parent.left == z:
                z.parent.left = x
            else:
                z.parent.right = x
        # 2. x의 left child로 z 지정
        x.left = z
        z.parent = x
        # 3. x의 원래 left child노드인 b를 z의 right child로 이동
        z.right = b
        if b: # b가 None이 아니라면
            b.parent = z
        # 이렇게 윗 레벨로 올라간 x 노드가 루트라면 새 루트 노드 지정
        if self.root == z:
            self.root = x

A = BalancedBST()
A.insert(15)
A.insert(4)
A.insert(2)
A.insert(20)
A.insert(17)
A.insert(16)
A.insert(19)
A.insert(32)
A.root.pre_order() # 15 4 2 20 17 16 19 32
A.rotateRight(20)
A.root.pre_order() # 15 4 2 17 16 20 19 32

A.rotateRight(20) 의 결과