AVL 트리
모든 노드에 대하여 왼쪽 subtree와 오른쪽 subtree의 높이 차가 1 이하인 BST
-> 이 조건을 만족할 경우 트리의 높이 h를 최소로 유지할 수 있다.
Rebalancing
노드가 삽입/삭제됐을 때, 트리가 AVL 성질을 만족하는 지 판별 후, rotation을 통해 균형을 다시 잡는 과정을 거친다.
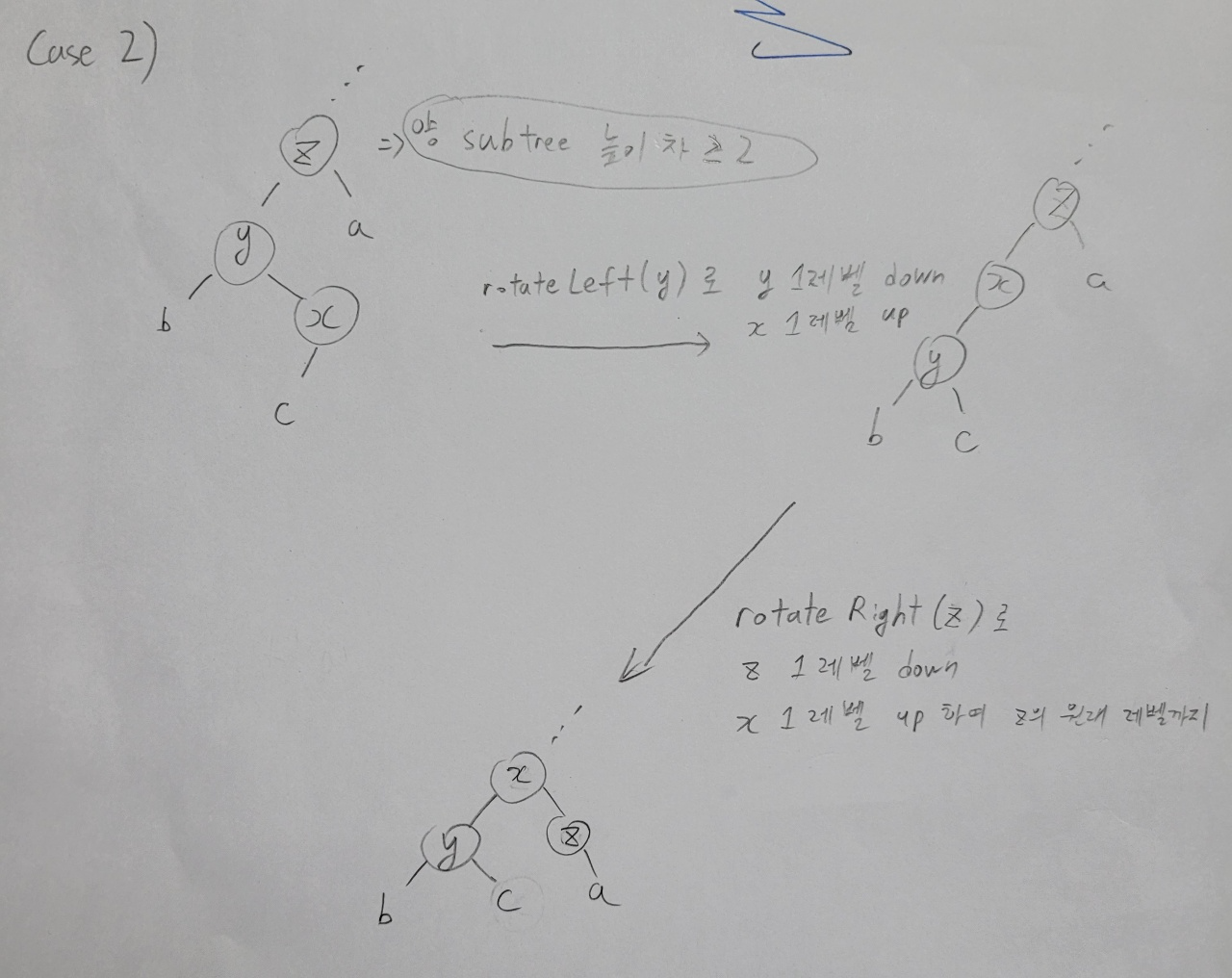
삽입/삭제된 노드로부터 parent노드로 올라가면서, AVL 성질이 최초로 깨지는 노드 z, z의 child노드 y, y의 child노드 x 에 대한 Rebalancing은 일반적으로 아래와 같다.
-
노드 z, y, x의 링크가 일직선일 경우 : Rotation 1회

-
노드 z, y, x의 링크가 굴절될 경우 : Rotation 2회
연산 & 수행시간
Insert(key) : BST의 insert 메서드를 상속하여 BST를 만족하는 위치에 노드 삽입 후, 그 노드의 parent노드들을 지정하여 AVL 균형을 맞춘다.
시간 복잡도는 BST의 insert 메서드 연산에 O(logN), 삽입된 노드부터 루트노드까지 균형을 확인하여 리밸런싱하는데 O(logN) 이므로, O(logN)
Delete(key) : BST의 deleteByMerging 혹은 deletebyCopying을 상속하여 삭제할 노드를 찾아 삭제하고, 그 부모 노드부터 루트까지 올라가면서 리밸런싱한다.
시간 복잡도는 BST의 삭제 연산에 O(logN), 리밸런싱에 O(logN)이므로, O(logN)
탐색연산의 경우, BST의 탐색연산을 그대로 상속하여 사용할 수 있으므로, O(logN)
Python 코드
노드 클래스에는 노드와 노드의 가장 깊은 leaf node 사이의 거리(깊이)를 구하는 depth 메서드와 이를 통해 양 subtree의 높이 차를 출력하는 balanceFactor 메서드를 추가했다.
class Node:
def __init__(self,key):
self.key = key
self.parent = None
self.left = None
self.right = None
#노드의 레벨 attribute 추가
self.height = 0
def __str__(self):
return str(self.key)
def pre_order(self): # M -> L -> R 순서로 전위순회
if self != None:
print(self.key)
if self.left:
self.left.pre_order()
if self.right:
self.right.pre_order()
def in_order(self): # L -> M -> R 순서로 중위순회
if self != None:
if self.left:
self.left.in_order()
print(self.key)
if self.right:
self.right.in_order()
def post_order(self): # L -> R -> M 순서로 후위순회
if self != None:
if self.left:
self.left.post_order()
if self.right:
self.right.post_order()
print(self.key)
# 노드에서 가장 깊은 child노드부터 parent노드까지의 거리(=subtree의 높이)
def depth(self):
if self.left:
l = self.left.depth()
else: l = 0
if self.right:
r = self.right.depth()
else: r = 0
return max(l,r) + 1
#서브트리 양쪽의 depth의 차이를 구함
def balanceFactor(self):
if self.left:
l = self.left.depth()
else: l = 0
if self.right:
r = self.right.depth()
else: r = 0
return abs(l - r)AVL 클래스는 BST 클래스를 상속한 BalancedBST 클래스를 상속하고, 리밸런싱과 삽입/삭제 연산을 추가하였다.
class AVL(BalancedBST):
def insert(self,key):
x = super(AVL,self).insert(key) # AVL의 상위 클래스인 BST의 insert 그대로 상속해서 호출
y = x.parent if x else None
z = y.parent if y else None
self.rebalance(x,y,z)
def rebalance(self,x,y,z):
while z:
if z.balanceFactor() >= 2:
if y == z.right:
if x == y.right:
self.rotateLeft(z)
if y.parent == None:
self.root = y
else: # x == y.left:
self.rotateRight(y)
self.rotateLeft(z)
if x.parent == None:
self.root = x
else: # y == z.left:
if x == y.left:
self.rotateRight(z)
if y.parent == None:
self.root = y
else: # x == y.right:
self.rotateLeft(y)
self.rotateRight(z)
if x.parent == None:
self.root = x
if self.root == y or self.root == x: break
x = x.parent
y = y.parent
z = z.parent
return self.root
def delete(self,key):
v = super(AVL,self).deleteByMerging(key)
z = v
y = None
x = None
#삭제한 노드의 parent부터 시작하여 균형이 깨지는 z를 우선 구하고,
#subtree의 높이 차를 case별로 나눠 z의 child인 y와 x를 지정하였다.
while z.balanceFactor() >= 2:
if z.right == None:
y = z.left
elif z.left == None:
y = z.right
elif z.left.depth() >= z.right.depth():
y = z.left
else: y = z.right
if y.right == None:
x = y.left
elif y.left == None:
x = y.right
elif y.left.depth() >= y.right.depth():
x = y.left
else: x = y.right
# 루트노드에 도달했을 때, 거슬러올라온 subtree의 반대쪽 subtree에서
# y, x가 잡혀 리밸런싱이 필요한 경우가 있기 때문에
# 루트노드를 z로 지정하여 리밸런싱을 한번 더 거친다.
z = self.rebalance(x,y,z)
B = AVL()
B.insert(10)
B.insert(5)
B.insert(15)
B.insert(2)
B.insert(7)
B.insert(11)
B.insert(30)
B.insert(4)
B.insert(25)
B.insert(40)
B.insert(27)
B.root.pre_order() # 10 5 2 4 7 25 15 11 30 27 28 40
B.delete(7)
B.root.pre_order() # 25 10 4 2 5 15 11 30 27 28 40
