분할 정복 (Divide and Conquer)
직접 해결할 수 있을 정도로 간단한 문제가 될 때까지 문제를 재귀적으로 쪼개나간 다음 그 하위 문제의 결과들을 조합하여 원래 문제의 결과를 얻어낸다.
대표적인 예로 병합 정렬 (Merge Sort) 가 있다.
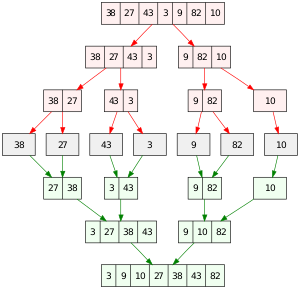
그림 출처 : https://en.wikipedia.org/wiki/Merge_sort
Merge Sort Pseudo code
MergeSort(A[], p, n){
if (p < q){
q = ⌊n / 2⌋
MergeSort(A, p, q)
MergeSort(A, q + 1, r)
Merge(A, p, q, n)
}
}
Merge(A[], p, q, n){
//A 정렬
T = [], t = 0, i = p, j = q + 1
while(i <= q and j <= n){
if A[i] < A[j]
T[t++] = A[i++]
else
T[t++] = A[j++]
}
while(i <= q)
T[t++] = A[j++]
while(j <= n)
T[t++] = A[j++]
A = T
return A
}분할 정복 수도코드
function F(x):
if F(x)가 간단 then:
return F(x)를 계산한 값 (정복)
else:
x를 x1, x2로 분할
F(x1)과 F(x2)를 호출
return F(x1)과 F(x2)로 F(x)를 구한 값 (분할 & 조합)Leetcode 169. Majority Element
길이 n인 숫자들의 리스트 nums에서 개수가 ⌊n / 2⌋개 이상인 숫자를 구하라.
nums에서 개수가 과반수가 넘는 숫자는 무조건 있다고 가정한다.
Example 1:
Input: nums = [3,2,3]
Output: 3
Example 2:
Input: nums = [2,2,1,1,1,2,2]
Output: 2
풀이 1. Counter 객체 이용
Counter 객체로 원소 수를 구한다. 가장 개수가 많은 원소를 return해도 상관없다.
코드
class Solution:
def majorityElement(self, nums: List[int]) -> int:
c = collections.Counter(nums)
return [i for i in c if c[i] > int(len(nums)/2)][0]
풀이 2. 분할 정복 이용
분할을 한다. 원소 개수가 0이면 None, 1개면 해당 원소를 return 한다.
이게 앞서 말한 정복이다.
2개부터는 리스트를 절반으로 자른 후 재귀적으로 return되는 값을 받는다. return할 때에는 개수가 과반이 되는 원소를 return 하도록 한다.
코드
class Solution:
def majorityElement(self, nums: List[int]) -> int:
if not nums: return None
if len(nums) == 1: return nums[0]
h = len(nums) // 2
a = self.majorityElement(nums[:h])
b = self.majorityElement(nums[h:])
return [b, a][nums.count(a) > h]
풀이 2. 파이썬다운 방식
정렬 후 가운데 원소 return
코드
class Solution:
def majorityElement(self, nums: List[int]) -> int:
return sorted(nums)[len(nums) // 2]
Leetcode 241.
어떤 수식이 string으로 주어진다. 이 수식에서 괄호를 묶는 경우에 따라 결과가 달라진다. 가능한 결과의 리스트를 return하라
Example 1:
Input: expression = "2-1-1"
Output: [0,2]
Explanation:
((2-1)-1) = 0
(2-(1-1)) = 2
Example 2:
Input: expression = "2*3-4*5"
Output: [-34,-14,-10,-10,10]
Explanation:
(2*(3-(4*5))) = -34
((2*3)-(4*5)) = -14
((2*(3-4))*5) = -10
(2*((3-4)*5)) = -10
(((2*3)-4)*5) = 10
풀이
- *+- 연산자를 기준으로 분할한다.
- 숫자만 있는 str으로 분할되면 숫자를 정수형으로 return 한다. (정복)
- 조합에서는 오른쪽 반환값과 왼쪽 반환값을 연산자를 이용해 연산한다.
- 재귀적으로 돌리면 최종 결과가 나오게 된다.
for문을 돌면서 어느 연산자를 먼저 기준으로 놓고 분할할 건지에 대해 모든 경우가 계산된다.
코드
class Solution:
def diffWaysToCompute(self, expression: str) -> List[int]:
def compute(left, right, op):
results = []
for l in left:
for r in right:
results.append(eval(str(l) + op + str(r)))
return results
if expression.isdigit():
return [int(expression)]
results = []
for index, value in enumerate(expression):
if value in "*+-":
left = self.diffWaysToCompute(expression[:index])
right = self.diffWaysToCompute(expression[index + 1:])
results.extend(compute(left, right, value))
return results