Dynamic Programming

작은 문제의 해결 결과를 저장해두었다가 나중에 큰 문제의 결과와 합하여 풀이하는 알고리즘
즉 최적 부분 구조를 갖는 문제에 적용할 수 있음
DP는 중복된 하위 구조의 해를 이용함

Leetcode 509. Fibonacci Number

정수 n이 주어질 때, n번째 피보나치 수를 구하는 문제

풀이 1. 재귀함수 이용

코드

class Solution:
  def fib(self, n: int) -> int:
    if n < 2: return n
    return self.fib(n-1)+self.fib(n-2)

단점

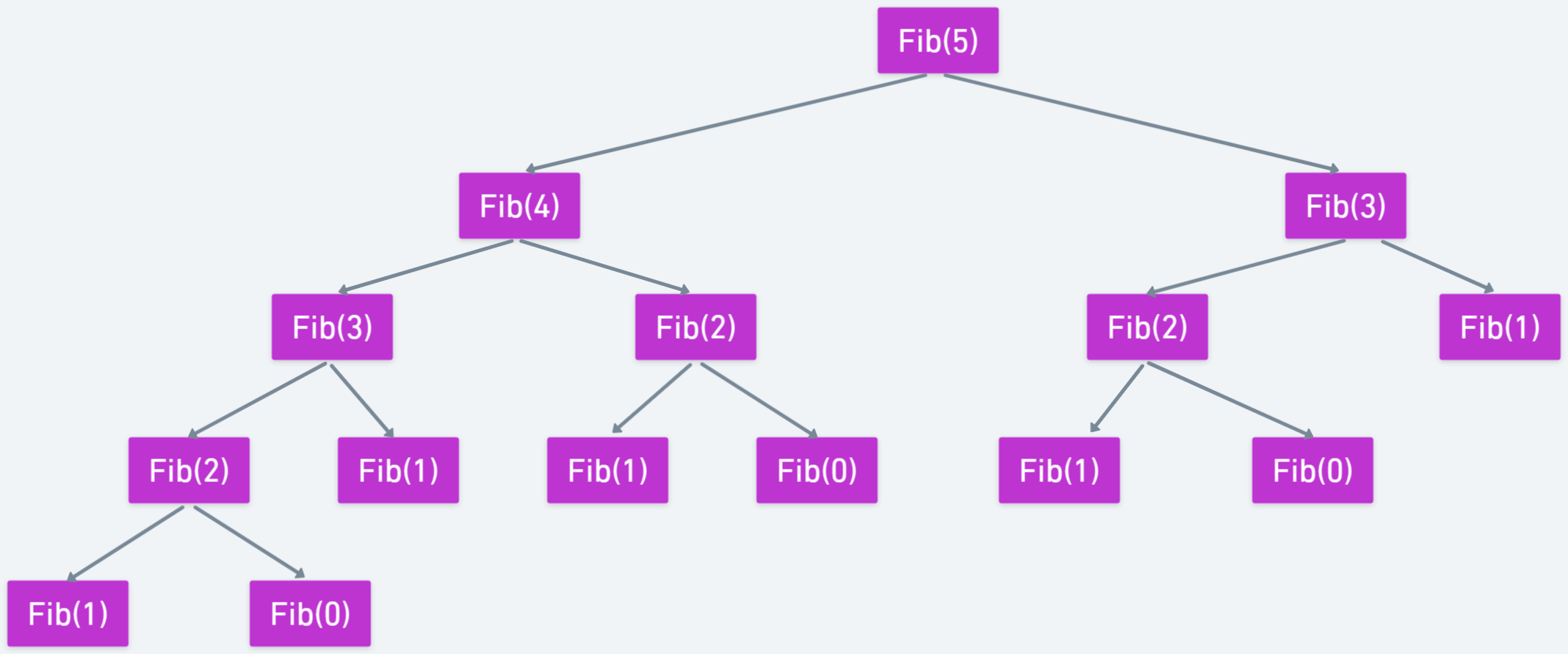
같은 피보나치 수의 호출이 너무 많다. 매우 오래걸린다.

풀이 2. DP bottom-up 방식 이용

코드

class Solution:
	def fib(self, n: int) -> int:
		dp = []
		for i in range(n + 1):
			if i < 2: dp.append(i)
			else: dp.append(dp[i - 1] + dp[i - 2])
		return dp[n]

풀이 3. DP bottom-up 방식 변수 두 개 이용

코드

class Solution:
	def fib(self, n: int) -> int:
    	if n < 2: return n
		a, b = 0, 1
		for i in range(2, n):
			a, b = b, a+b
		return a+b

풀이 4. DP memoization 방식 이용

이미 계산한 피보나치 수는 바로 꺼내 쓰고 호출하지 않도록 함

코드

class Solution:
    dp = collections.defaultdict(int)
    def fib(self, n: int) -> int:
        if n <= 1:
            return n
        if self.dp[n]:
            return self.dp[n]
        self.dp[n] = self.fib(n-1) + self.fib(n-2)
        return self.dp[n]

Leetcode 53. Maximum Subarray

정수의 리스트 nums가 주어질 때, sum이 가장 큰 sub array를 구하고 그 sum을 반환하라.

Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: [4,-1,2,1] 의 합 6이 가장 큼

Input: nums = [1]
Output: 1
Explanation: [1]이 가장 큼

Input: nums = [5,4,-1,7,8]
Output: 23
Explanation: [5,4,-1,7,8] 의 합 23이 가장 큼

풀이 1. Dynamic Programming

(이전까지 계산된 값) & (계산된 값과 현재시점의 배열의 합) 중 큰 값을 저장

코드

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        dp = [nums[0]]
        for i in range(1, len(nums)):
            dp.append(max(nums[i], nums[i]+dp[i-1]))
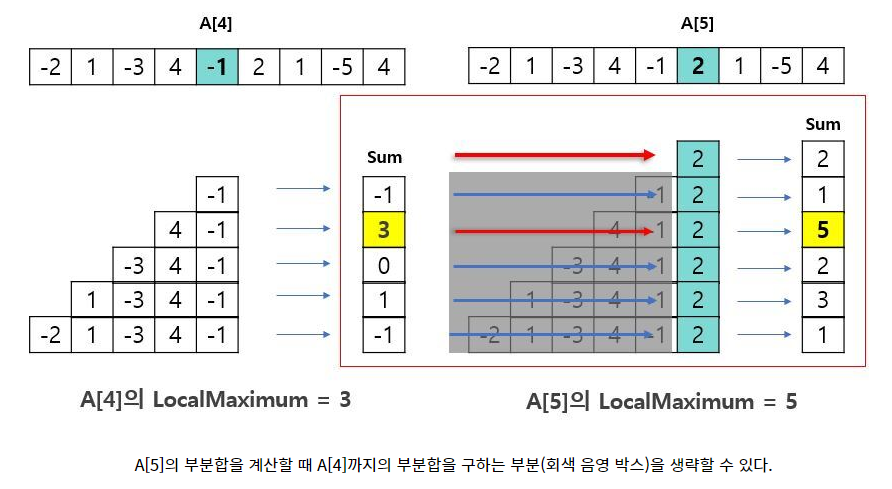
        return max(dp)

풀이 2. Kadane's algorithm

핵심 : 이전까지 계산된 값은 무조건 optimal한 결과값이다.

(그림 출처 : https://sustainable-dev.tistory.com/23)

코드

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        localmax, globalmax = nums[0], nums[0]
        for i in range(1, len(nums)):
            localmax = max(localmax + nums[i], nums[i])
            if localmax > globalmax: globalmax = localmax
        return globalmax

Leetcode 70. Climbing Stairs

계단을 오르는데, 하나 혹은 두 계단씩 오를 수 있다고 하자.
n 개의 계단을 오르기 위한 경우의 수를 구하시오

예) n = 3, answer = 3
(1, 1, 1) or (2, 1) or (1, 2)

풀이

n=1 : (1) 1가지 경우
n=2 : (1, 1) or (2) 2가지 경우
n=3 : (1, 1, 1) or (2, 1) or (1, 2) 3 가지 경우
n=4 : (1, 1, 1, 1) or (2, 1, 1) or (1, 2, 1) or (1, 1, 2) or (2, 2) 5 가지 경우

...

n=k : n=k-1일 때 경우의 수 + n=k-2일 때 경우의 수

코드

class Solution:
    def climbStairs(self, n: int) -> int:
        if n <= 2: return n
        a, b = 1, 2
        for i in range(3, n):
            a, b = b, a+b
        return a + b

비고

프로그래머스 비슷한 문제
https://school.programmers.co.kr/learn/courses/30/lessons/12900
https://school.programmers.co.kr/learn/courses/30/lessons/12902

Leetcode 198. House Robber

도둑이 길을 따라 나란히 지어진 집들을 털려고 한다. 근데 한 집을 털고 바로 그 옆집을 털게 되면 경보가 울린다. 어떻게 하면 돈을 가장 많이 털 수 있을까? - 최소 한 집씩 건너서 털어야 한다.

Example 1)
Input: nums = [1,2,3,1]
Output: 4
Explanation: 1번째 집과 3번째 집을 턴다. (1 + 3 = 4)

풀이 1. Dynamic Programming

dp[0] = nums[0],
dp[1] = max( nums[0], nums[1] )
...
dp[k] = max( dp[k-1], dp[k-2]+nums[k] )

코드

class Solution:
    def rob(self, nums: List[int]) -> int:
        if len(nums) <= 2: return max(nums)
        dp = [nums[0], max(nums[:2])]
        for i in range(2, len(nums)):
            dp.append(max(dp[i - 1], dp[i - 2]+nums[i]))
        return dp[-1]