CTFS(연속시간 푸리에급수)

Kkoaa·2022년 2월 15일
신호및시스템

신호 및 시스템

목록 보기
3/4

앞서 CTFT에 대한 식을 유도해보았다.

X(f)=∫−∞∞x(t)e−j2πftdtX(f) = \int_{-\infty}^\infty x(t) \mathrm{e}^{-j2{\pi}ft}\mathrm{d}t

이 때, x(t)x(t)가 T의 주기를 가진다고 하자. 그러면 위 적분구간 중에서 T만큼만 적분하고 무한대로 더하면 푸리에 변환이 가능해질 것이다.

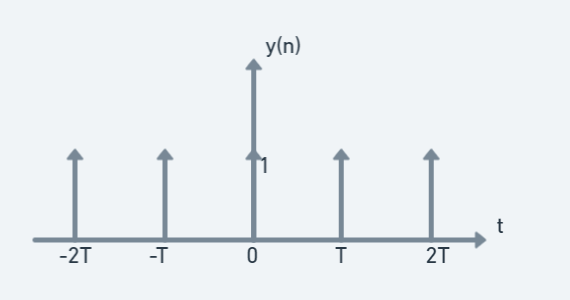
T가 주기인 위에 있는 함수는 델타 함수의 합으로 표현할 수 있다.

∑k=−∞∞δ(t−kT)\displaystyle\sum_{k={-\infty}}^{\infty} \delta(t-kT)

이 함수를 살짝 변형해보면

1T∑k=−∞∞δ(f−kT)\frac{1}{T}\displaystyle\sum_{k={-\infty}}^{\infty} \delta(f-\frac{k}{T})

이는 한 주기 T 안에서 무수히 많은 델타 함수를 촘촘히 곱하는 것이다.

X(f)=∫−T2T2x(t)e−j2πftdt×1T∑k=−∞∞δ(f−kT)X(f) = \int_{-\frac{T}{2}}^{\frac{T}{2}} x(t) \mathrm{e}^{-j2{\pi}ft}\mathrm{d}t \times \frac{1}{T}\displaystyle\sum_{k={-\infty}}^{\infty} \delta(f-\frac{k}{T})
=1T∫−T2T2x(t)e−j2πftdt×∑k=−∞∞δ(f−kT)= \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} x(t) \mathrm{e}^{-j2{\pi}ft}\mathrm{d}t \times \displaystyle\sum_{k={-\infty}}^{\infty} \delta(f-\frac{k}{T})

이때 1T∫−T2T2x(t)e−j2πftdt\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} x(t) \mathrm{e}^{-j2{\pi}ft}\mathrm{d}t 전체를 aka_k라 하고 이를 Fourier Coefficient(푸리에 계수)라고 한다.

이를 Inverse Fourier Transform식에 넣어보자.

x(t)=∫−∞∞X(f)ej2πftdf=∫−∞∞∑k=−∞∞akδ(f−kT)ej2πftdfx(t) = \int_{-\infty}^\infty X(f) \mathrm{e}^{j2{\pi}ft}\mathrm{d}f = \int_{-\infty}^\infty \displaystyle\sum_{k={-\infty}}^{\infty} a_k\delta(f-\frac{k}{T}) \mathrm{e}^{j2{\pi}ft}\mathrm{d}f
=∑k=−∞∞ak∫−∞∞δ(f−kT)ej2πftdf=∑k=−∞∞akej2πft= \displaystyle\sum_{k={-\infty}}^{\infty} a_k \int_{-\infty}^\infty \delta(f-\frac{k}{T}) \mathrm{e}^{j2{\pi}ft}\mathrm{d}f = \displaystyle\sum_{k={-\infty}}^{\infty} a_k \mathrm{e}^{j2{\pi}ft}

이것이 Fourier Series이다. 정리하면

Fourier Series :
x(t)=∑k=−∞∞akej2πftx(t)=\displaystyle\sum_{k={-\infty}}^{\infty} a_k \mathrm{e}^{j2{\pi}ft}\\
where ak=1T∫−T2T2x(t)e−j2πftdta_k = \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} x(t) \mathrm{e}^{-j2{\pi}ft}\mathrm{d}t

profile
Kkoaa
냠냠
이전 포스트

CTFT(연속시간 푸리에변환)

다음 포스트

DTFT(이산시간 푸리에변환)

0개의 댓글