신호 및 시스템
1.Convolution
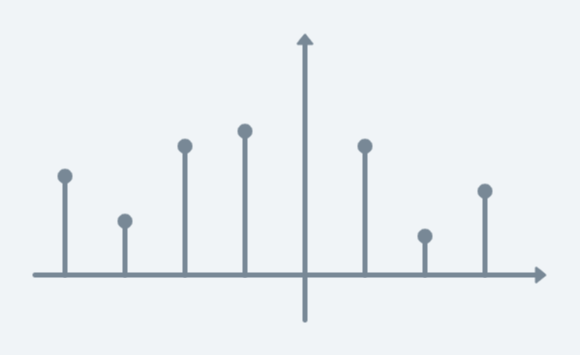
위와 같은 이산 신호 $x(n)$이 있다 하자. 위 그림에서 각 index k에 있는 값들은 dirac delta함수를 사용하여 $x(k)\\times\\delta(n - k)$으로 나타낼 수 있다. 즉$$ x(n) = \\displaystyle\\sum\_{k=-\\
2022년 2월 15일
2.CTFT(연속시간 푸리에변환)

일반적으로 CTFS를 먼저 배우고 CTFT를 배우는데, 교수님께서 반대로 하는 것이 이해하는데 좀 더 쉬울 것이라고 하셔서 CTFT를 먼저 포스팅한다. 음 결론부터 말하면 나는 CTFS를 먼저 이해하였다...ㅎㅎ
2022년 2월 15일
3.CTFS(연속시간 푸리에급수)
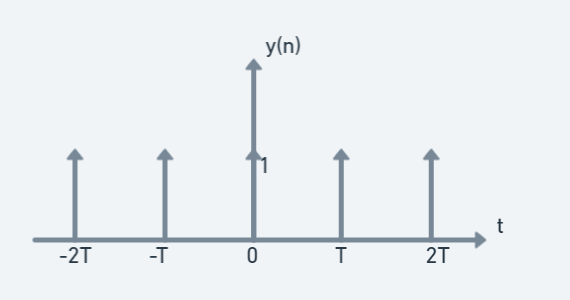
앞서 CTFT에 대한 식을 유도해보았다.$$X(f) = \\int\_{-\\infty}^\\infty x(t) \\mathrm{e}^{-j2{\\pi}ft}\\mathrm{d}t$$이 때, $x(t)$가 T의 주기를 가진다고 하자. 그러면 위 적분구간 중에서 T만큼만
2022년 2월 15일
4.DTFT(이산시간 푸리에변환)
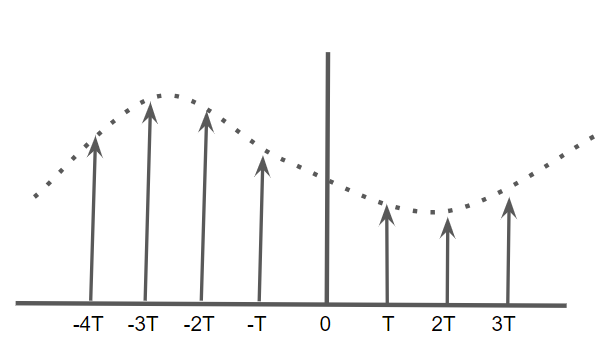
앞서 CTFT를 먼저 보고 CTFT식으로부터 CTFS를 유도하였다. 마찬가지로 DTFT의 식을 구한 후 DTFS를 유도해보는 과정을 진행하기로 한다. 사실 DTFT는 CTFT에서 각 지점을 샘플링한 것과 동일하다.마치 샘플링하는 것과 같다. 어떤 연속신호 $x(T)$
2022년 2월 16일