원래 이산신호 그래프는 점으로 표기해야 하지만, 점으로 표시하기 좀 깔끔해보이지 않아서 다음과 같이 표현하였다.
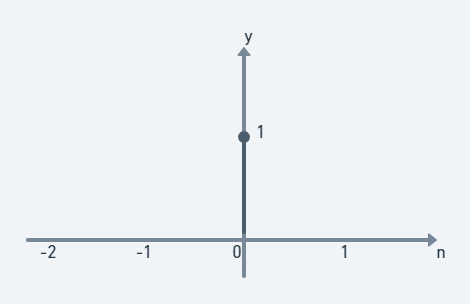 Discrete time에서 dirac delta 함수의 모습, n=0일때 1이고 0이 아닌 구간의 값은 모두 0이다.
Discrete time에서 dirac delta 함수의 모습, n=0일때 1이고 0이 아닌 구간의 값은 모두 0이다.
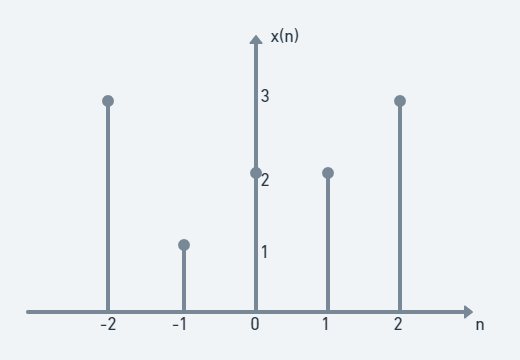
위와 같은 이산 신호 x(n) = [ 3, 1, 2, 2, 3 ]이 있다 하자. 위 그림에서 각 index k에 있는 값들은 dirac delta함수를 사용하여 x(k)×δ(n−k)으로 나타낼 수 있다. 예를 들어 x(1)=x(1)×δ(n−1)로 나타낼 수 있다. 즉
x(n)=k=−∞∑∞x(k)δ(n−k)
이 때, 위 x(n) 신호를 LTI시스템 H에 넣는다고 하자. 그 때 H의 출력 y(n)을 구해보자.
y(n)=H{x(n)}=H{k=−∞∑∞x(k)δ(n−k)}
시스템 H 가 LTI 시스템이므로 "superposition"에 의해 k=−∞∑∞x(k)가 밖으로 빠져나올 수 있다.
H{k=−∞∑∞x(k)δ(n−k)}=k=−∞∑∞x(k)H{δ(n−k)}
Impulse Resopnse Function
dirac delta함수를 LTI시스템의 입력으로 넣으면
H{δ(n)}=h(n)
이 때, δ(n)은 impulse function이 되고
시스템의 출력 h(n)을 impulse resopnse function이라고 한다.
따라서 y(n)은 최종적으로
y(n)=k=−∞∑∞x(k)H{δ(n−k)}=k=−∞∑∞x(k)h(n−k)
가 된다. 이는 convolution으로 나타낼 수 있고 기호로 x(n)∗h(n) 과 같이 나타낸다.
DT에서의 convolution과 CT에서 convolution은 모두 똑같다. 단지 차이는 ∑과 ∫의 차이일 뿐이다. CT에서 convolution을 나타내보면
y(t)=∫−∞∞x(τ)h(t−τ)dτ
Convolution 계산
어떤 신호 x(n)과 y(n)의 convolution을 보다 쉽게 계산하는 방식이 있다.
아래와 같은 이산 신호 x(n) = [3, 1, 2, 2, 3]과 y(n) = [2, 1, 1]이 있다 가정하자. 값이 없는 구간은 모두 0이라 하자.
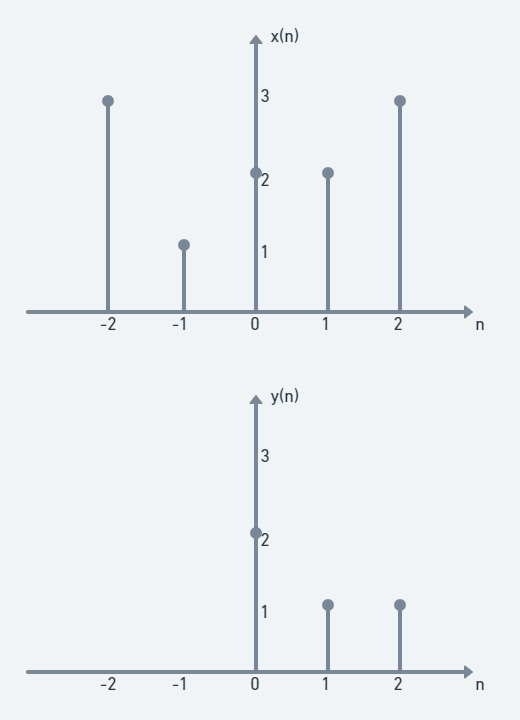
이때, convolution x(n)∗y(n) 을 구하는 과정은다음과 같다.
- y(n)을 y축에 대칭이 되도록 뒤집는다 -> y(-n)을 구한다.
- x(n)의 제일 왼쪽과 y(n)의 제일 오른쪽을 맞닿아 맞춰준다. index는 x의 index를 따라간다.
- 오른쪽으로 한 칸씩 옮겨가며 겹치는 부분의 sum을 구한다.
차례로 구해보자. y(−n)을 구하면
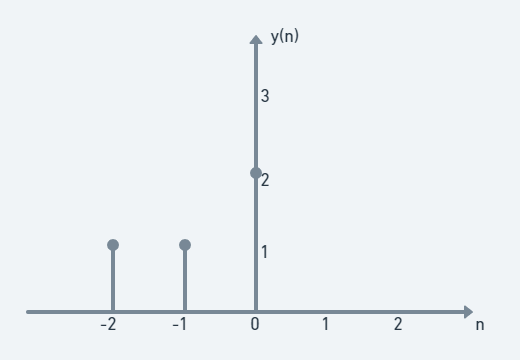
y(−n) = [1, 1, 2]가 된다. 이제 이를 x(n)과 차례로 겹쳐가며 sum을 구해보자.
(step 1)
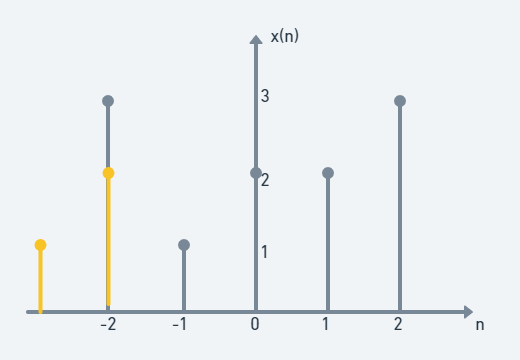
노란색이 y(−n)이다. 겹치는 부분은 index -2에서 밖에 없으므로 2×3=6이다.
(step 2)

-2와 -1에서 겹친다. 3×1+2×1=6
(step 3)
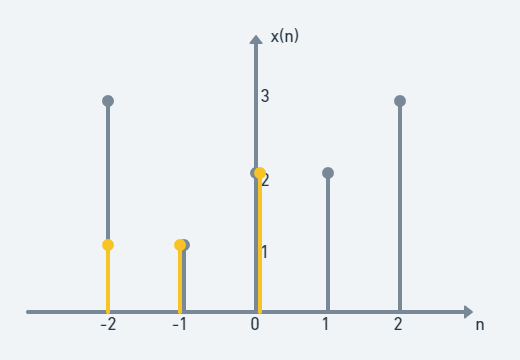
-2와 -1, 0에서 겹친다. 3×1+1×1+2×2=8
(step 4)
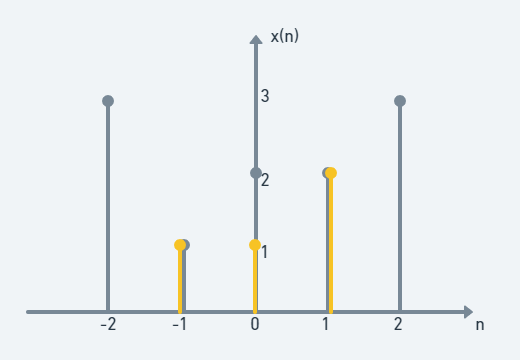
1×1+2×1+2×2=7
(step 5)
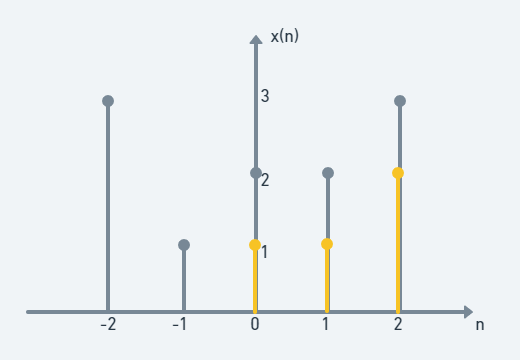
2×1+2×1+3×2=10
(step 6)
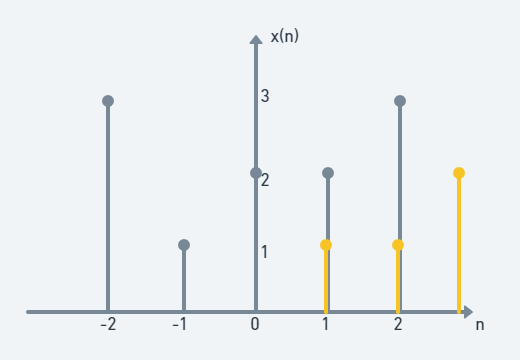
2×1+3×1=6
(step 7)
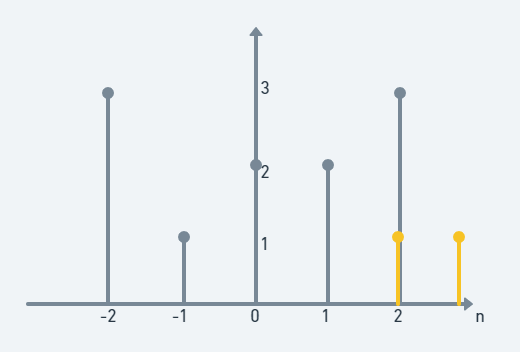
3×1=3
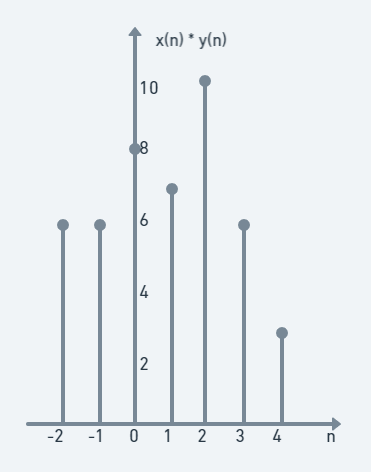
이를 종합해보면 x(n)∗y(n) = [6, 6, 8, 7, 10, 6, 3]인 것을 확인할 수 있다.
 Discrete time에서 dirac delta 함수의 모습, n=0일때 1이고 0이 아닌 구간의 값은 모두 0이다.
Discrete time에서 dirac delta 함수의 모습, n=0일때 1이고 0이 아닌 구간의 값은 모두 0이다.