D-Seperation

어떤 그래프에서 한 번에 독립(Independence)를 알 수 있을까?
만약 어떤 그래프에서 노드 X가 노드 Y에게 영향을 준다면(influences) 그건 독립이 아닐 것이다.

Common Cause(Common Parent)

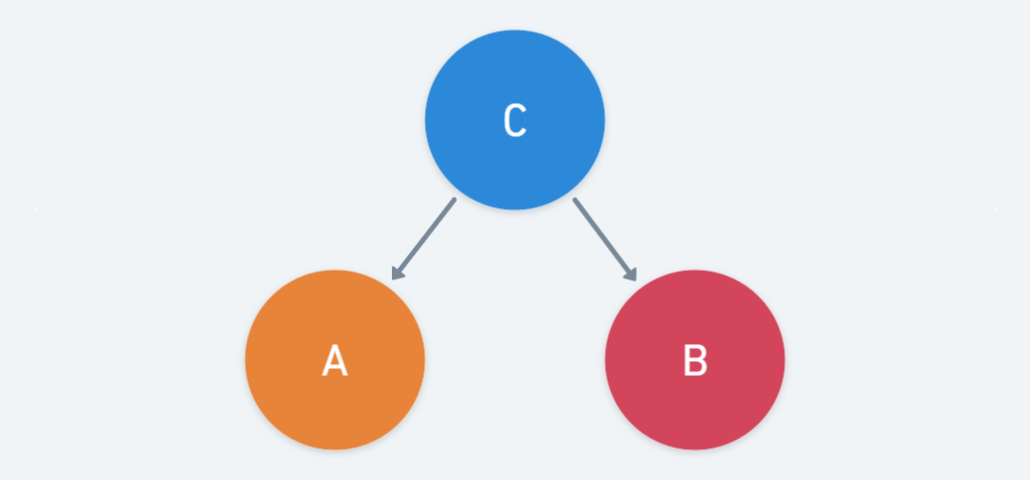
Bayesian Network에서 보았듯이 C가 주어질 때 A와 B는 조건부 독립이다.($A\perp B | C$)

Causal/Evidential Trail

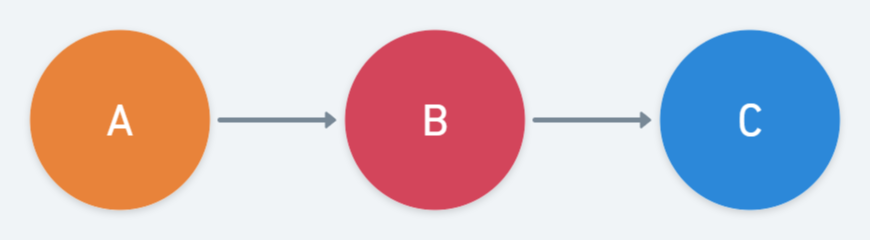
일렬로 이루어진 그래프이다. A에서 C까지 path로 이어져있다.

B가 주어지지 않으면 (B is not observed) A에서 B를 통해 C에게 영향을 주기 때문에 A와 C는 독립이 아니다.

그런데 B가 주어지면 (B observed) B가 바로 C와 연결되므로 A는 더 이상 C에게 의미가 없어진다. 즉 B가 주어질 때 A와 C는 조건부 독립이다. ($A\perp C | B$)

Evidential Trail은 Causal의 반대 케이스이다. C의 입장에서는 B가 주어지면 굳이 A를 알 필요가 없으므로 마찬가지 결과가 나온다.

Common Effect

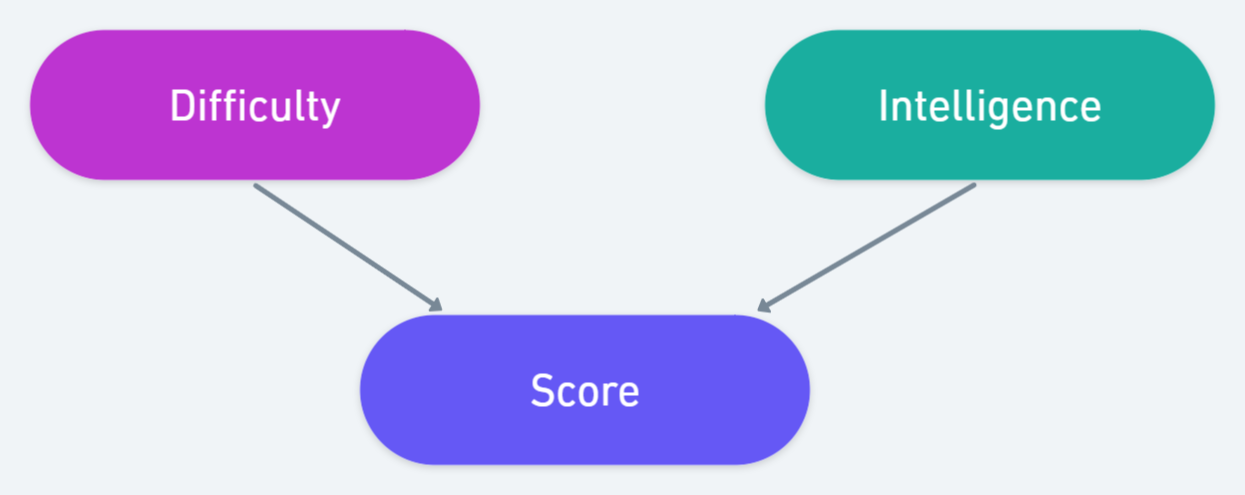
부모 노드가 2개인 경우를 v-structure라 한다. 위에서 한 학생의 지능 I와 시험의 난이도 D에 의해 점수 S가 매겨진다 하자.

1. S가 주어지 않으면 (not observed) : 시험의 난이도를 알아도 학생의 지능을 알 수 없다. 반대로 학생의 지능을 알아도 시험의 난이도는 알 수 없다. 따라서 D와 I는 독립

2. S가 주어지면 (observed) : 학생의 점수가 100점 만점에 20점이라 하자. 분명 낮은 점수이다. 이 때, 시험의 난이도가 low라면 시험이 쉬운데도 D-를 맞은 것이니 그 학생의 지능는 낮다고 볼 수 있다. 이 경우, 더 이상 시험의 난이도와 학생의 지능은 연관이 없다고 볼 수 없다. 즉 S가 주어지면서 D와 I 사이에 관계가 생겨나게 된 것이다. ($D\perp I | S$)

위 그림과 같은 경우를 생각해보자. 어떤 학생의 Grade가 D-라 하면, 낮은 학점을 받은 것이다. 즉 Score 역시 low일 것이다. 즉 Grade가 주어지면 Score도 추론이 가능하므로 자연스럽게 D와 I는 조건부 독립이 된다.($D\perp I | G$)

Active & Blocked

어떤 그래프에서 노드 Z를 통해 노드 X가 노드 Y에 영향을 줄 때, trail X <=> Z <=> Y는 Active이다. 반대로 영향을 주지 않으면 그 trail은 Blocked이다.
(조건부 독립이 성립 : Blocked, 성립되지 않음 : Active)

trail(path) : 이웃한 노드들끼리 연결되어 있는 sequence

D-Seperation

notation : $d-sep_G(X;Y|Z)$

정의 : 그래프 G에 X,Y,Z의 세 가지 노드들의 집합이 있다 하자. 만약 Z가 주어질 때, Z를 통해 이어지는 X와 Y사이의 active한 trail이 있으면 D-Seperation이다.

D-Seperation이 발견되면 X와 Y는 Z에 의해 조건부 독립이 성립된다.

How to check D-Seperation?

1. edge의 방향과 상관없이 X와 Y사이에 모든 path를 찾는다.
2. 해당 path가 Z와 descendant 노드들에 의해 blocked되었는지 확인한다.
3. 모든 path가 blocked 되었으면, D-Seperation이다.

Example

다음 그래프에서 D-Seperation을 찾고 해당 문제가 조건부 독립이 성립될지 알아보자.

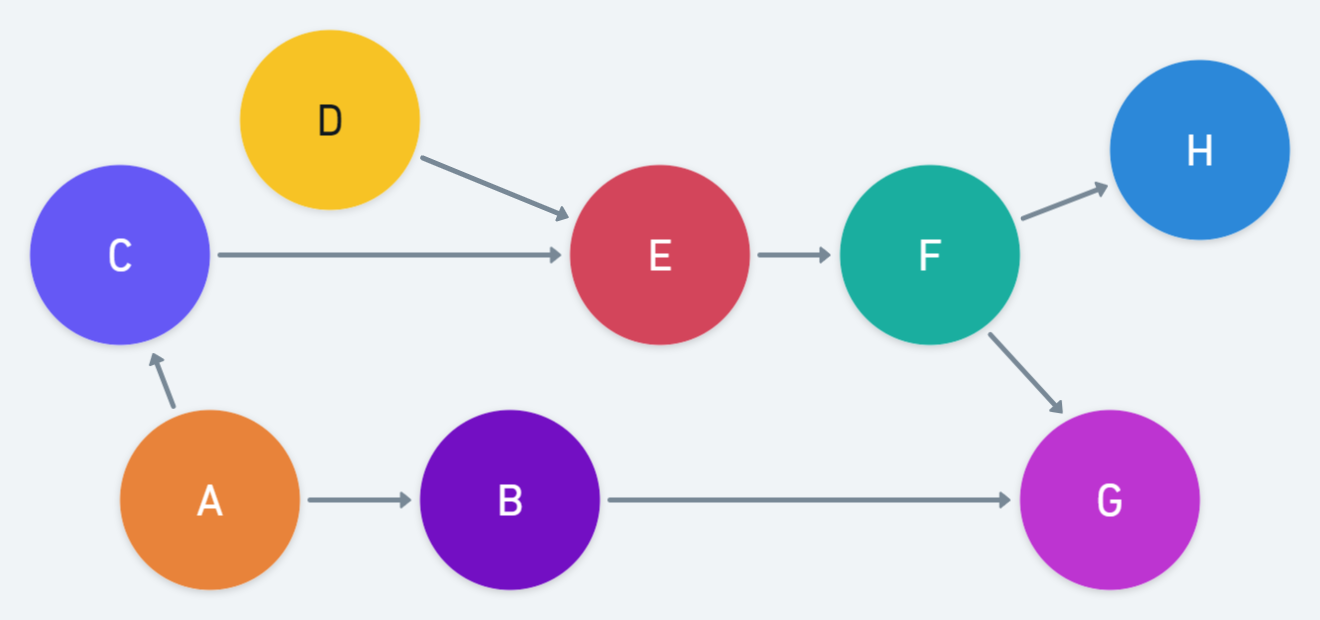
1. ($B \perp C | A$)?

우선 B에서 C까지 path를 모두 찾는다.

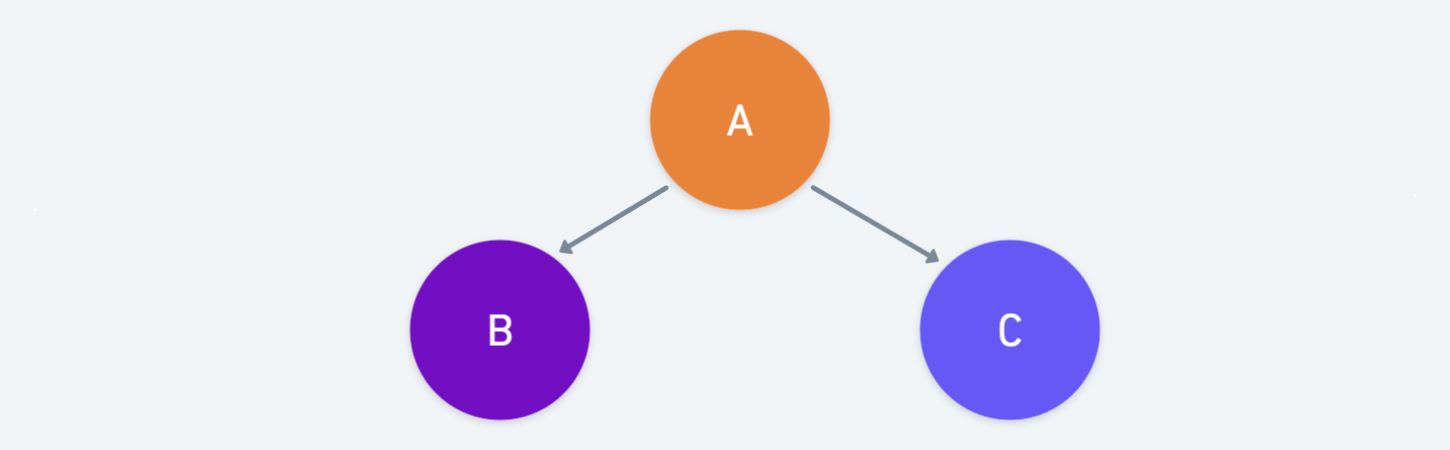
첫 번째 path를 위와 같이 찾았다. A가 주어질 때 B와 C는 독립이므로 blocked 된다.

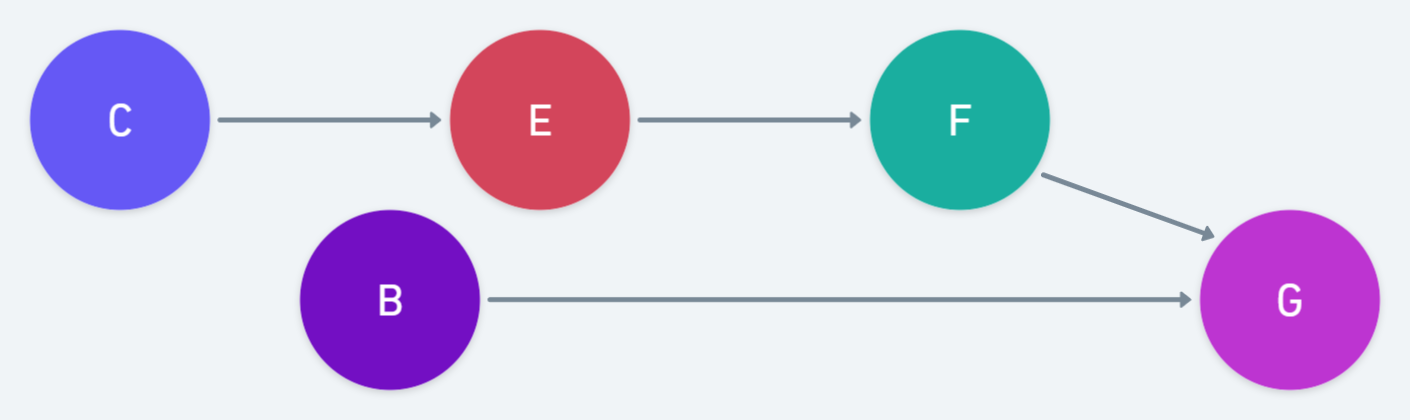
B - G - F에서 Common Effect이다. 하지만 G는 주어지지 않았으니 B - G - F는 blocked 이다. C - E - F가 common cause이므로 해당 path 역시 Blocked 되었다.

A가 주어졌을 때 모든 경로가 blocked 이므로 D-Seperation이 발생하였다. 즉 ($B \perp C | A$)이다.

2. ($A \perp F | E$)?

A - F 사이의 모든 path를 찾는다.

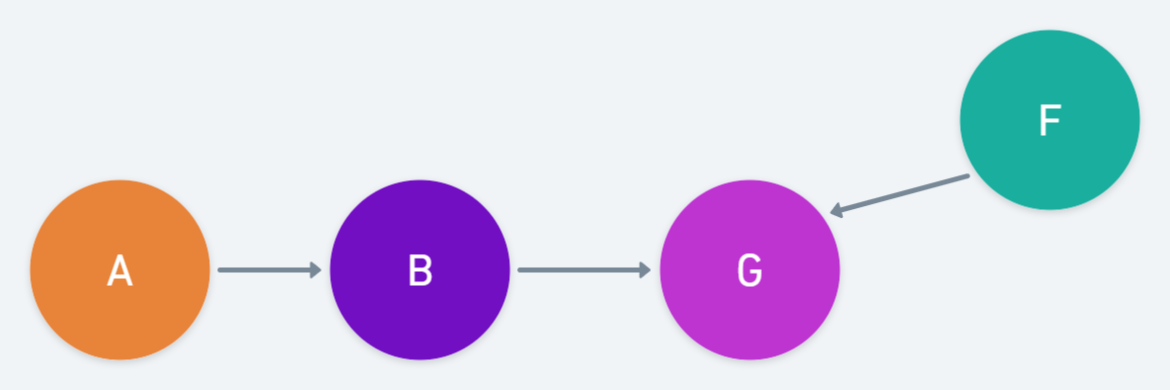
B - G - F에서 G가 주어지지 않았으므로 B-G-F는 blocked되었고 A -> B이므로 A-B-G-F는 blocked 된다.

C - E - F가 Causal trail이다. 이 때, E가 주어졌으므로 C와 F가 독립이 된다. 따라서 A와 F도 독립이 된다. 즉 A - C - E - F는 blocked된다.

E가 주어졌을 때 모든 경로가 blocked 이므로 D-Seperation이 발생하였다. 즉 ($A \perp F | E$)이다.

3. ($C \perp D | F$)?

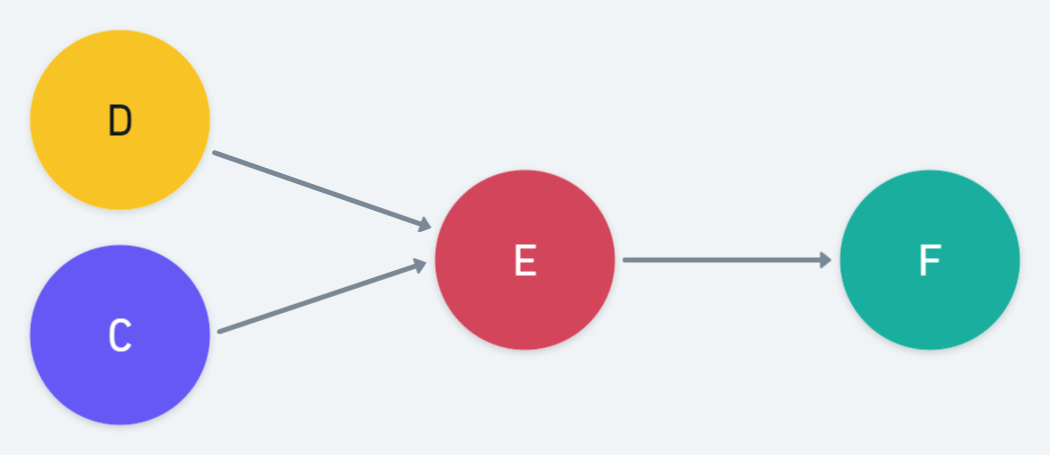
Common Effect이다. F가 주어지게 되면 C와 D는 서로 관련이 된다. 독립이 성립되지 않으므로 다음의 경로는 active가 된다. 즉 D-Seperation이 생겨나지 않는다!