Markov Random Field

Bayesian Network와 Undirectrd Graph의 특성을 비교해보면서 이해하는 것이 좋다

Directed Graph vs Undirected Graph

Directed Graph

• edge를 통해서 노드들(Random Variables) 사이에 인과성이 주어짐.
• Bayesian Network에서 봤듯이 결합 확률 분포 P를 조건부 확률로 나타낼 수 있음.

Undirected Graph

• 노드들 사이에 대등한 상관관계가 주어짐.
• 조건부 확률을 쓸 수 없으므로 potential function(factor)를 통해 분포를 나타냄.

Cliques

• 어떤 그래프 G에서 fully connected된 subgraph.

• Maximal clique : clique 중 가장 노드가 많은 clique.

  Example

  

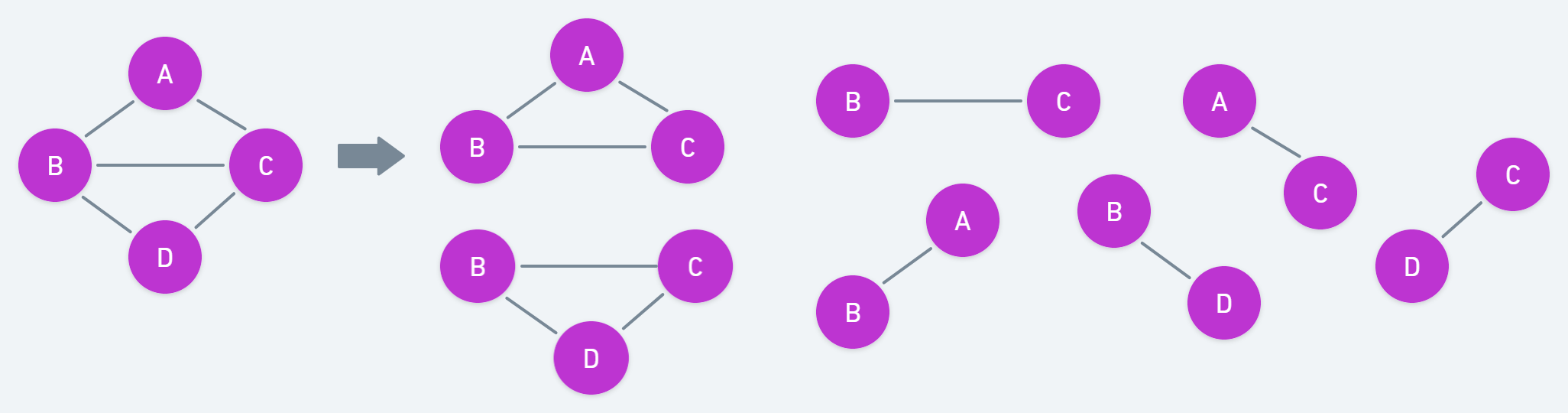
다음과 같이 여러 개의 clique들이 존재한다. 노드가 한 개인 경우도 clique에 해당하지만, PGM에서는 노드들 사이에 관계를 중요시하기도 하고 학습하는 과정에서 크게 의미가 없어 보통 고려를 하지 않는다.

Gibbs(Boltzmann) Distribution

UGM(Undirected Graph Model)에서 distribution을 표현하는 방법이다. 어떤 UGM H의 distribution $P(X_1, ... , X_n)$ 는 다음과 같이 나타낼 수 있다.

$P(X_1, ... , X_n) = \frac{1}{Z}\Pi_{c\in C}{\phi_c(X_c)}$
$Z=\Sigma_{X_i, ..., X_n}\Pi_{c\in C}{\phi_c(X_c)}$
$c$=clique of graph, $\phi_c$=potential function associated with cliques

이 때, P를 Gibbs(Boltzmann) Distribution 이라고 한다. 즉 Markov Random Field에서 Distribution P는 그래프 g의 clique 들의 곱으로 나타내어진다는 것이다.

Potential function $\phi_c$

앞서 말했듯이, UGM에서는 CPT를 못 쓰기 때문에 potential, 또는 factor라 불리는 값을 사용한다. 이 값은 확률이 아니다. 따라서 합이 1, 값은 0과 1 사이와 같은 확률의 특성을 따르지 않아도 된다. 음수여도 되고, 큰수여도 되고, 단지 의미하는 것은 Random Variables 사이의 상대 척도(compatibililty)가 된다.

partition function

partition function Z는 확률분포 P의 합이 1이 되어야하므로 나눠주는 값이다. normalize한다고 생각하면 된다. 이 때, Z를 구하기 위해서는 $2^n$의 연산이 필요하다($X_1$ 부터 $X_n$까지 모든 경우를 더해주어야 하기 때문)

Markov Independence

Global M.I : $sep_H(A; C | B)$

자주색 노드의 집합을 B, B를 기준으로 왼쪽 회색 노드 집합을 A, 오른쪽을 C라 하자. B가 양 옆의 A와 C를 seperate함. 즉 $(A \perp C | B)$

Local M.I : { $X_i \perp V - X_i- MB_{X_i} | MB_{X_i}$ }

자주색 노드 X_i 의 neighbor인 보라색 노드들이 X_i와 나머지 회색 노드들을 분리. 이 때, 보라색 노드가 Markov Blanket이다.

이렇게 보면 확실히 BN보다 UGM에서 Independence를 이해하는게 더 쉽다.

Hammersley-Clifford Theorem

P가 강한 양의 분포값을 가질 때(strictly positive), Random Variable V = {$X_1 ... X_n$}로 구성된 UGM H가 있으면, 다음 세 가지 조건은 동치이다.

• P(x)는 Max-Clique에 의해 인수분해되는 Gibbs Distribution이다.
• local Markov Property
• Global Markov Property

이것이 의미하는 것은 Gibbs Distribution은 결국 Markov Random Field의 특성을 만족한다는 것이다. 즉 조건부 확률의 정보가 자동으로 주어진다는 것이다.