I-map in Bayesian Network

Recap

I-map : 확률분포 P와 그래프 G가 있을 때, $I(G) \subseteq I(P)$를 만족하는 것. 이 때, $I()$는 확률분포(혹은 그래프)에 존재하는 모든 독립의 집합을 의미한다.

Minimal I-map

가장 단순한 I-map으로 다음 두 조건을 만족할 때가 minimal I-map이다.

• G는 P의 I-map $(I(G) \subseteq I(P))$
• 만약 G'이 G에 속하는 진부분집합일때 $(G' \subset G)$ G'은 더이상 P의 I-map이 아니어야 한다. $(I(G') \not\subseteq I(P))$

이를 확인하는 방법이 있다. $I(G) \subseteq I(P)$를 만족하는 그래프 G에서 edge 하나를 지웠을 때 P에 없는 독립관계가 생겨나면(새로운 독립 관계가 생겨나므로 더이상 $I(G) \subseteq I(P)$를 만족하지 않는다) G는 P의 minimal I-map이다.

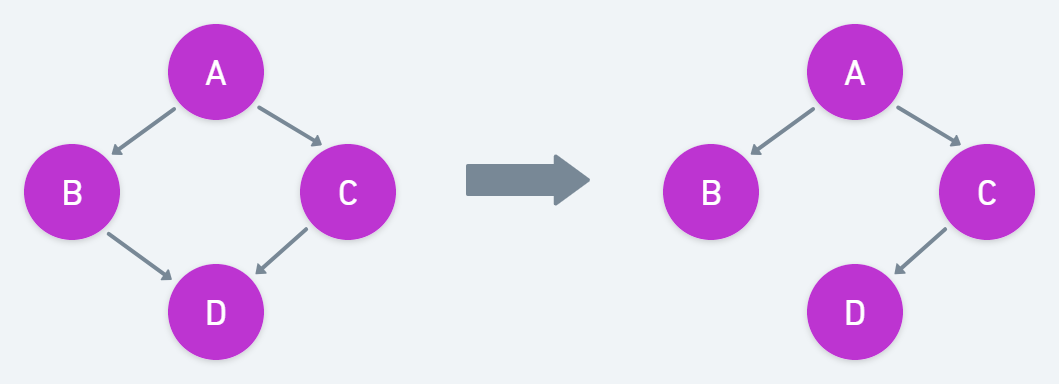
feature of minimal I-map

1. 모든 확률분포 P는 minimal I-map을 가지고 있다.
2. 모든 확률분포 P에서 유일한 minimal I-map은 없다(node ordering에 따라 여러 minimal I-map 존재 가능).

I-Equivalence

어떤 BN 그래프 G와 G'에 대해서 $I(G) = I(G')$, 즉 모든 독립조건이 같을 때 I-equivalence를 만족한다.

skeletons of BN

edge의 구조를 의미한다. 다음 세 그래프는 skeleton이 같다고 볼 수 있다.

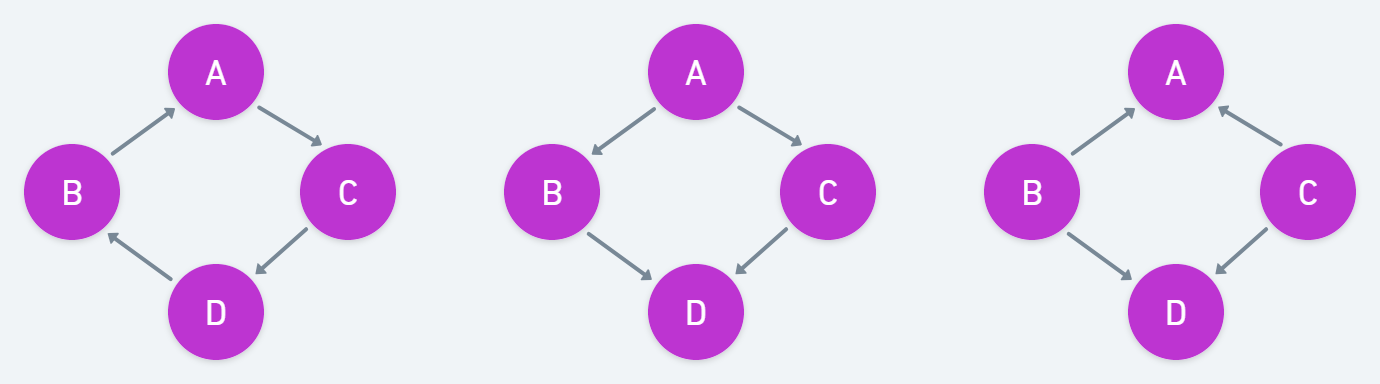
I-Equivalence는 두 그래프의 skeleton이 같아야 한다.
하지만 skeleton이 같다 해서 두 그래프가 I-equivalence를 만족하지는 않다.
다음 두 그래프는 skeleton이 같지만, 독립 관계가 다른 그래프이다.

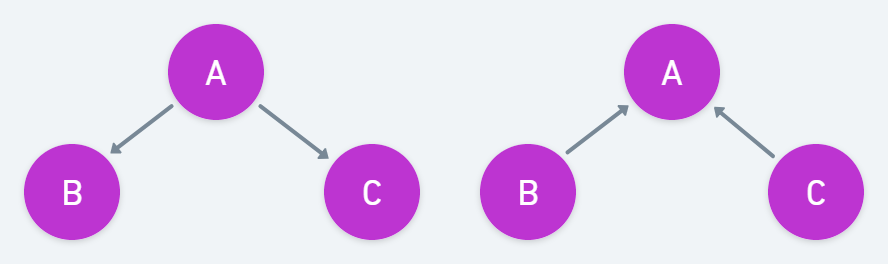
P-map(Perfect I-map)

어떤 DAG G에 대해 다음 두 조건을 만족할 때가 P-map이다.

• $I(G) = I(P)$(독립 집합이 완전 같아야 함)
• $X \perp Y | Z$ 와 $d-sep_G(X;Y|Z)$가 동치

feature of P-map

• 모든 확률분포가 다 P-map인 그래프를 가지지는 못한다.
• 어떤 그래프에서는 유일한 P-map인 그래프가 존재한다(단, 그래프가 I-equivalence를 만족해야 한다).

Morality and Immorality

moral : V-structure에서 부모 노드끼리 연결이 된 경우
immoral : V-structure에서 부모 노드끼리 연결이 안 된 경우

Theorems

• 그래프 G와 G'이 같은 skeleton이고 같은 V-structure를 가진다면, $I(G) = I(G')$이다(반대는 성립 불가능)
• $I(G) = I(G')$이면 G와 G'이 같은 skeleton이고 같은 V-structure를 가진다.(반대도 성립)