CNN & Feature Map & Kernel

Feature Map

: 입력으로부터 커널을 사용하여 합성곱 연산을 통해 나온 결과
-> 목적: 각각의 특성들을 패턴으로 읽어 내는 것

Feature Map (==Basis function)
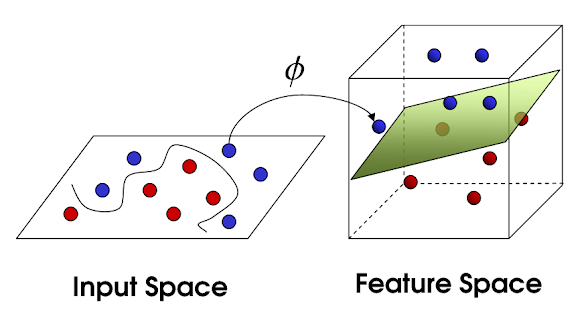
위 그림처럼 linear model f(x)로 sample을 분류할 수 없을 때, input space x를 linear model이 해결할 수 있는 형태인 feature space $\phi$(X)로 만들면 문제를 해결할수 있다.

이 때, 사용한 함수 $\phi$(피)를 기저함수(basis function) 혹은 feature map이라고 한다.

정리하자면, $\phi$는 비선형 특징을 갖는 input space를 선형 특징을 갖는 feature space로 변환해주는 함수이다.

feature map과 kernel trick은 같은게 아니다. (뒤에 나옴)

자세한건 <참고: https://sonsnotation.blogspot.com/2020/11/11-1-kernel.html > 여길 보자..

Kernel

$\phi$를 정의하기도 어렵고, 문제를 풀기위한 연산량도 너무 많다.
이 문제를 해결하기 위해 고안된 것이 kernel이다.

kernel의 목적

• 고차원 변환
• 내적 연산량 문제 해결

그리고 이미 증명된 다양한 kernel들이 공개 돼 있다. 즉 우리는 $\phi$가 어떤 함수인지 몰라도 되고, $\phi$를 내적할 수있는 kernel을 갖다 쓰면 된다.

결국 Kernel은 두 벡터의 내적이며, 기하학적으로 cosine 유사도를 의미하기 때문에 similarity function이라고도 불린다.

그리고 이 함수들을 이용한 Linear technique을 Kernel Trick이라고 한다.

CNN의 전반적인 과정

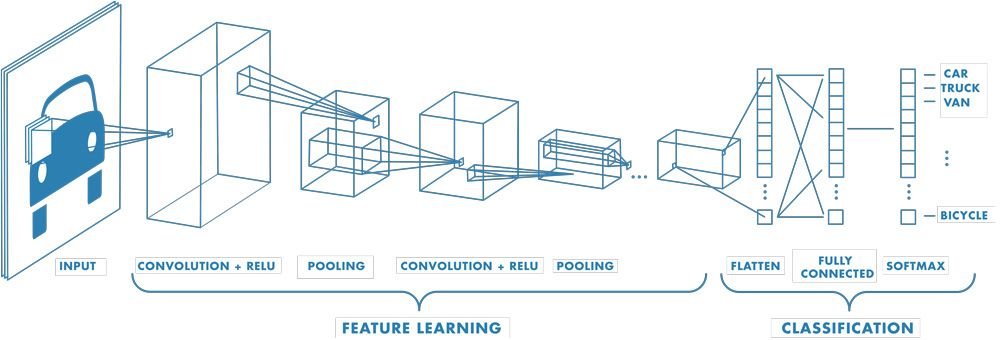
여러 컨벌루션 계층이 있는 신경망의 예. 각 훈련 영상에 서로 다른 해상도의 필터가 적용되고, 컨벌루션된 각 영상은 다음 계층의 입력으로 사용됩니다.

Convolution이란?

Convolution: 하나의 함수와 또 다른 함수를 반전 이동한 값을 곱한 다음, 구간에 대해 적분하여 새로운 함수를 구하는 수학 연산자

1D Convolution: $y[n] = \sum_{k=-\infty}^\infty h[n-k] x[k]$

<출처: https://pasus.tistory.com/21 >


2D Convolution: 커널을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조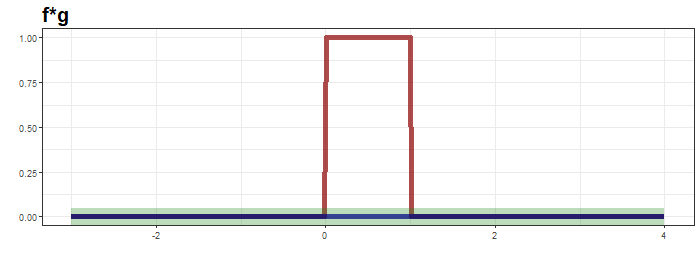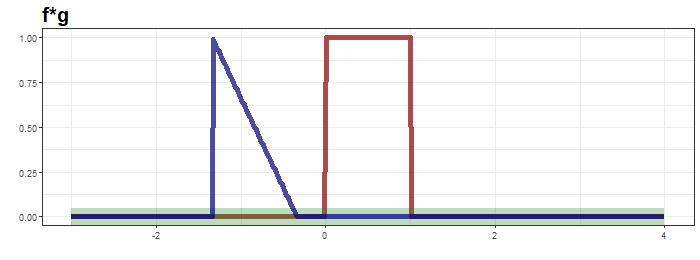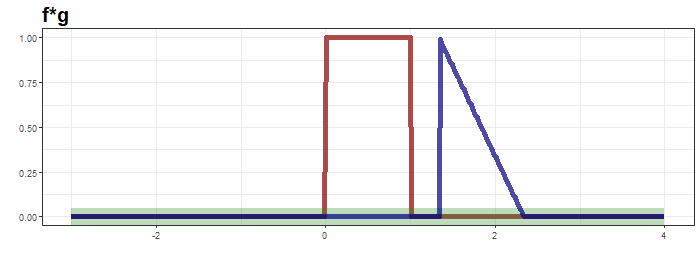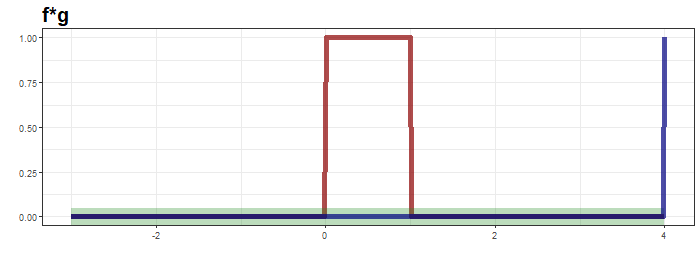주의할점: 행렬곱이 아닌 각 자리에 위치한 값들을 각각 곱하는 element-wise 연산

<출처:
https://sonsnotation.blogspot.com/2020/11/11-1-kernel.html
https://yjjo.tistory.com/8 >