고유값, 고유벡터, 선형변환

고유 벡터 (EigenVector)

• 선형 변환이 일어난 후에도 방향이 변하지 않는 0이 아닌 벡터

계산

고유값 (EigenValue)

• 고유 벡터의 길이가 변하는 배수를 선형 변환의 그 고유 벡터에 대응하는 고유 값

고유벡터와 고윳값이 물어보는 것:

“벡터 x에 어떠한 선형변환 A를 했을 때, 그 크기만 변하고 원래 벡터와 평행한 벡터 x는 무엇인가요?”
“그렇다면, 그 크기는 얼마만큼 변했나요?”

선형 변환과 고유값, 고유벡터

행렬은 선형 변환 연산이다.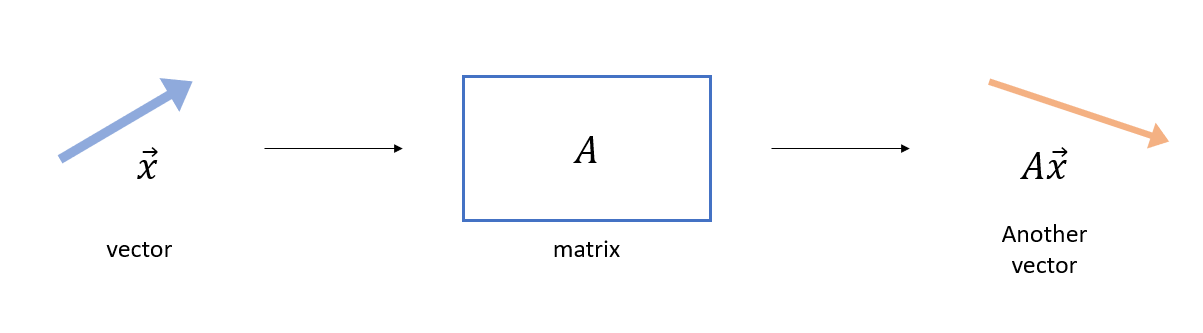

그래서 어떤 벡터에 행렬을 곱했을 때 방향, 크기 모두 변할 수 있다.

이 때, 특정 벡터와 행렬은 선형변환을 취해주었을 때, 크기만 변하고 방향은 바뀌지 않는다.

ex) [1,1]$^T$ -> [[1,2],[2,1]] -> [3,3] $^T$

즉, A$\vec{x}$ = $\lambda\vec{x}$ (선형 변환한 벡터 = 기존 벡터의 스칼라 배 라는 뜻)

그래서 n x n 행렬 A에 대해 0이 아닌 $\vec{x}$존재한다면, $\lambda$는 행렬 A의 고유값이다.
이 때, $\vec{x}$는 고유값 $\lambda$에 대응하는 고유 벡터이다

이를 만족하기 위한 해는 $(A-\lambda I) = 0$ (1), $\vec{x} = 0$ (2), 두 가지 인데

(2)만 만족하는 경우 $\lambda$가 아무거나 들어와도 된다.
그리고 (1)이 $\vec{x}$의 역행렬이 되면 안되는데 ($A*A^{-1}=E\neq0$)

을 만족하면 된다.

그래서 고유값과 고유벡터가 왜 중요한데?

결국에 고유값은 행렬의 고유 특성을 나타내는데, 이를 통해서 행렬이 어떤 변환을 수행하는지 이해할 수 있다.
또한, 고유값은 행렬의 대각화(diagonalization)에 필요한 정보를 제공한다.

고유벡터는 행렬의 주요한 변환 방향을 나타내며, 데이터의 주성분 분석과 같은 다양한 응용에서 중요한 역할을 한다.
또한 고유 벡터들은 서로 선형 독립적이고 기저(basis)를 형성하므로, 행렬을 대각화하고 행렬의 거듭제곱 등을 계산하는데 유용하게 사용된다.

고유값과 대각화

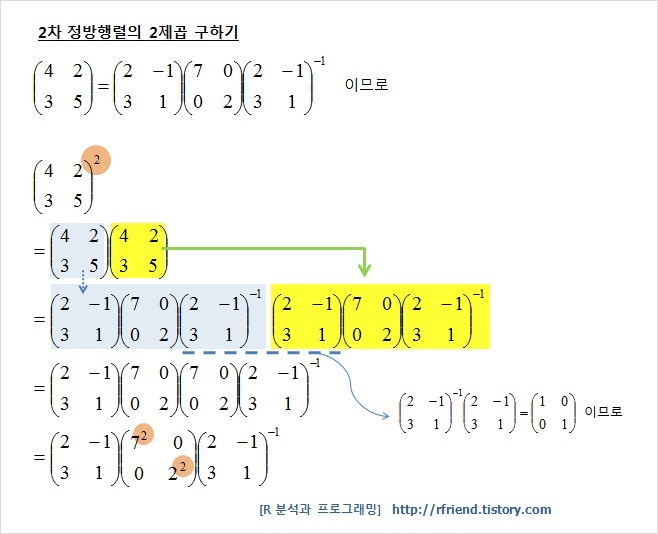
행렬의 대각화란?
주어진 행렬을 대각행렬로 변환하는 과정을 말하며 대각행렬이란 주 대각선을 제외한 모든 요소가 0인 특별한 형태이다.

대각화는 주로 선형 변환을 분석하거나 계산하기 쉽게 만들기 위해 사용되는데, 고유값과 고유벡터를 이용해 원래 행렬의 성질을 파악할 수 있다.

대각화된 행렬에서는 고유값이 주 대각선에 위치하고, 고유벡터들은 대응하는 열로 구성된다.

SVD에서의 고유값 사용

보통 svd를 할 때는 full svd가 아닌, truncated SVD를 사용하게 되는데 이는 원본 데이터 $A$에 대한 근사 $A^\prime$을 만들어준다. (자세한건 밑의 참고글 확인)

참고

• https://angeloyeo.github.io/2019/07/17/eigen_vector.html
• https://rfriend.tistory.com/182 (고유벡터 계산)
• https://rfriend.tistory.com/183 (고유벡터와 대각행렬 관계)
• https://darkpgmr.tistory.com/106 (SVD 사용)