Logistic Regression이 탄생한 이유와 필요한 이유 및 유도
Linear Regression
선형회귀에는 단순선형회귀와 다중선형회귀가 있다.
-
단순선형회귀
말 그대로 독립변수X 하나가 종속변수Y 하나에 어떻게 영향을 끼치는지?즉, x라는 독립변수의 결정계수 이 얼마인가에 따라 영향력이 얼마나 되는지...
-
다중선형회귀
여러개의 독립변수X가 1개의 연속형 종속변수 Y에 어떻게 영향을 미치는지?
(공차한계(Tolerance)와 분산팽창요인(VIF)를 확인해서 다중공선성을 고려해야 함)
일반적인 다중선형회귀에 대한 그래프는 아래와 같다.
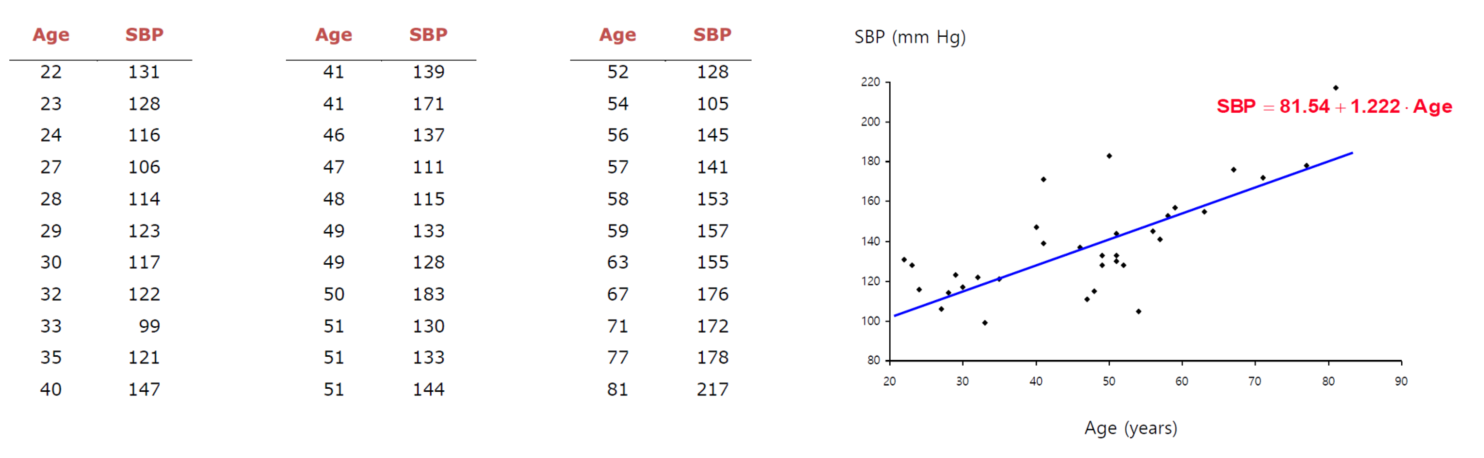
그러나 이걸 y를 범주형으로 가정할 경우 아래와 같은 이상한 그래프가 튀어나오게 되고 결국에 다중선형회귀로는 이를 정확하게 측정할 수 없다는 결론이 나온다.
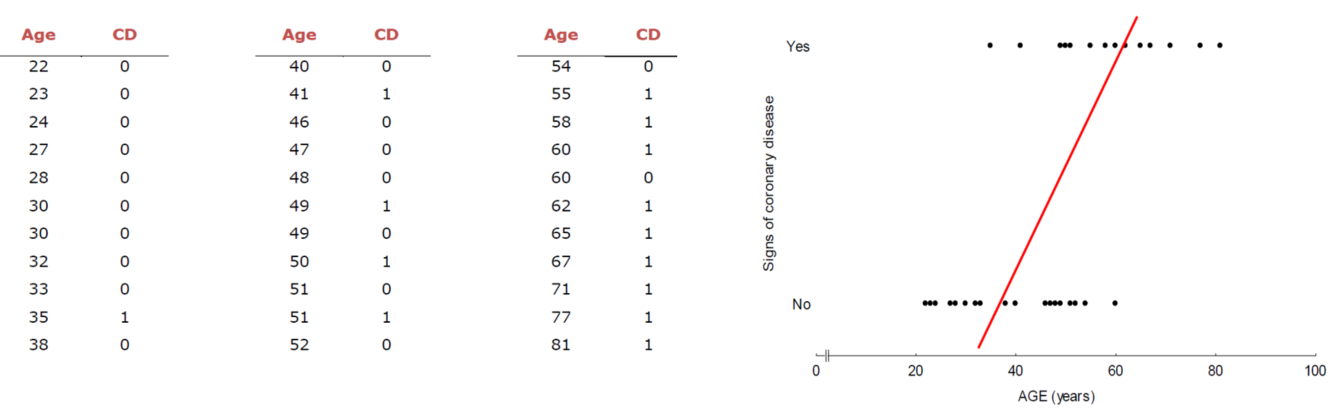
이를 해결하기 위해 범주형에 유의미한 Logistic Regression이 나오게 된다
Logistic Regression
실제 많은 자연, 사회현상에서는 특정 변수에 대한 확률값이 선형이 아닌 S-커브 형태를 따르는 경우가 많다. 이러한 S-커브를 함수로 표현해낸 것이 바로 로지스틱 함수이다. (분야에 따라 시그모이드 함수로도 불리기도 함)
로지스틱 함수는 x값으로 어떤 값이든 받을 수가 있지만 출력 결과는 항상 0에서 1사이 값이 된다. 즉 확률밀도함수(probability density function) 요건을 충족시키는 함수라는 이야기
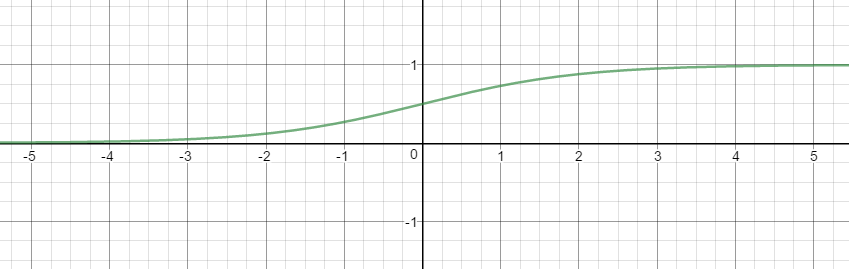
Odds(승산)
- 임의의 사건 A가 발생하지 않을 확률 대비 A가 발생할 확률
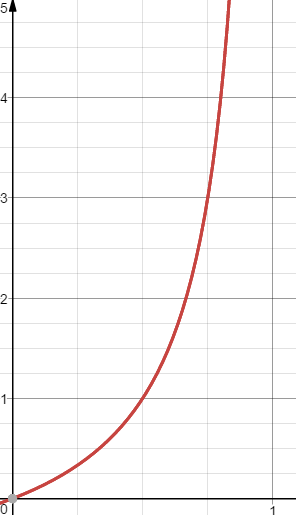 (x축: P(A), y축: odds)
(x축: P(A), y축: odds)
logistic regression의 기반이 되는 아이디어
기존 회귀식의 장점은 그대로 유지하고 종속변수 Y를 범주가 아니라 범주 1이될 확률로 두고 식을 세우면
이때 좌변은 위의 sigmoid함수에서 알 수 있듯이 0~1사이의 범주를 가진다.
그러나 기존 식은 (-, )이다.
그래서 좌변을 odds로 설정하면
이렇게 하면 좌변의 범위는 (0, )가 된다.
그래서 여기에 log를 취해주면 (== logit)
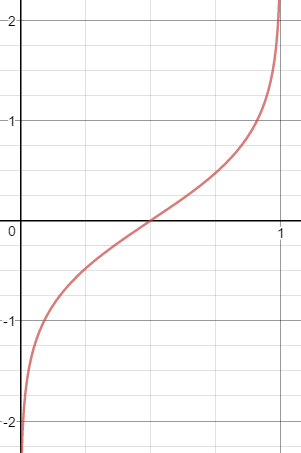
그래프를 얻을 수 있고, 이 때 범위는 (-, )가 된다.
이때, 의 의미는?
ex) 입력벡터 x의 첫번째 요소인 에 대응하는 회귀계수 이 학습결과 2.5로 정해진다고 가정하면 이 1단위 증가하면 범위 1에 해당하는 log odds가 2.5 커진다는 의미를 갖는다.
결론
Logistic Regression은 범주형 문제를 예측할 때 사용되는 다중선형회귀에서 odds (어떤 사건이 일어날 확률이 안일어날 확률의 몇배가 되는지)를 기반으로 추로하는 것
