베이지안 정리를 왜 하지?

베이지안 정리를 왜 쓰는가?에 대한 궁금증이 큰데, 이에 대해 자세하게 나와있는 블로그를 기반으로 정리해보자

Motivation

• 모델이 커질수록 해석하기가 어려워지고 해석하기 어려운 딥러닝 모델의 출력값을 얼마나 신뢰할 수 있는지 알기 어렵다
• 또한 모델이 정확한 예측을 하지 못하는 경우가 발생하곤 한다. 예를 들어 학습 데이터에 노이즈가 있었거나 학습에 사용하지 않은 데이터가 입력으로 들어오는 경우
• 따라서 딥러닝이 잘 모르는 것을(학습되지 않은 것을) 알게끔 하는게 중요한 문제가 되고 있다.

자세한 내용은 참고 블로그를 통해서 확인하면 더 쉽게 알 수 있다.

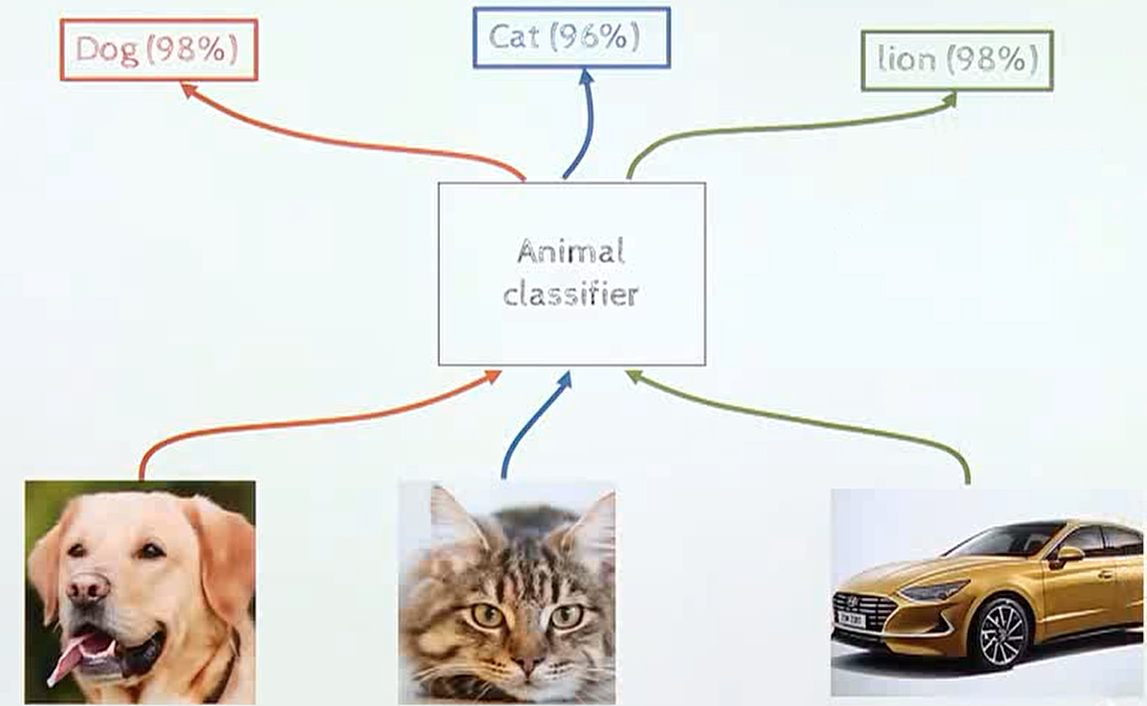
이러한 잘못된 인식을 over-confidence문제가 있기 떄문이라고 말을 하는데, over-confidence 문제의 이유는 다양한 원인 분석이 있다. 그 중 영향이 큰 원인 중 하나는 학습 데이터 자체가 over-confidence하도록 만들어 진다는 점이다.

따라서 딥러닝 시스템을 구축할 때, 딥러닝의 불확실성(uncertaninty)를 고려할 수 있는 시스템을 만드는 것이 중요하다.

이러한 불확실성을 고려할 수 있는 방안이 베이지안인 것이다.

베이지안

먼저 베이지안 방법론에 대한 의미는 다음과 같다.

• 베이즈 룰은 기존의 확률 관점인 빈도수(frequency)와는 다른 관점을 바라봄으로써 모델이나 현상에 대한 불확실성을 정량화하는 시도이다.

전통적인 확률 접근론인 빈도주의 관점에서 동전을 던지는 문제를 보면 동전을 무수히 던졌을 때, 앞면이 나올 빈도, 뒷면이 나올 빈도는 0.5로 수렴한다는 관점이며 수식으로는 $p(\theta)={1\over2}$와 같다.

만약 동전을 5번 던진 결과 앞면 3번, 뒷면 2번이 관측되었다는 가정을 해보자.
빈도주의 관점에서 동전의 앞면이 나올 확률은 $p(\theta)={3\over5}$이다


반면 베이지안 관점에서는 확률 자체를 불확실성으로 바라본다

위 식에 대하여 빈도주의 동전의 앞면이 나올 확률이 50%라고 단정짓지만 베이지안에서는 동전의 앞면이 나올 가능성이 50% 정도 라고 결론을 내린다. 즉 불확실성을 내포한다.

따라서 베이지안에서는 빈도주의와 같은 확률 모델을 계속 학습하여 고정된 참 값의 확률을 찾아가는 것이 아니라, 아래와 같이 불확실성을 내포한 확률 분포를 찾는 것이 목적이 된다.

빈도주의에서는 확률 값이 고정되기 때문에 어떤 확률값에 variance가 없이 고정이 되지만, 베이지안 에서는 정해진 확률 값이 없이 분포로 나타나고, 이 분포에는 variance가 존재하므로 불확실성을 내포하게 된다. 간단히 정리하면 불확실성의 정량화는 variance를 통해 나타나진다.

즉 베이지안의 핵심은 불확실성을 나타내는 확률 분포가 업데이트 된다는 것입니다.

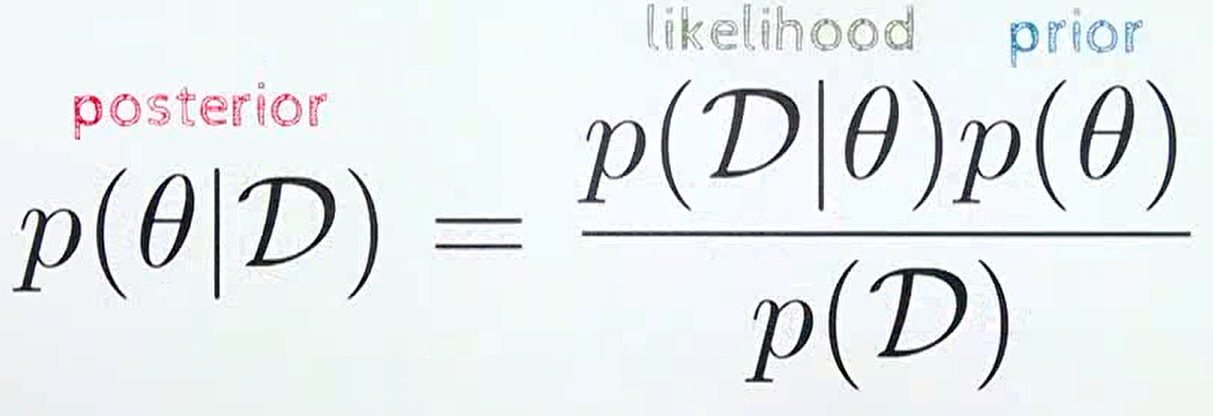
우리가 흔히 알고있는 베이즈 룰의 식을 다시 한번 생각해보면

• prior: 새로운 데이터 $D$를 관찰하기 전에 알고 있는 사전 분포에 해당. 앞에서 상식적으로 알고 있는 앞면이 나올 확률 0.5가 이에 해당한다.
• likelihood: 현재 확률 모델이 얼마나 데이터를 잘 설명하는 지 나타내는 정량화 된 값. 이 값은 빈도주의에서 살펴본 확률 표현 3/5에 해당한다.
• posterior: likelihood 값을 이용하여 prior → posterior로 업데이트 하는 것

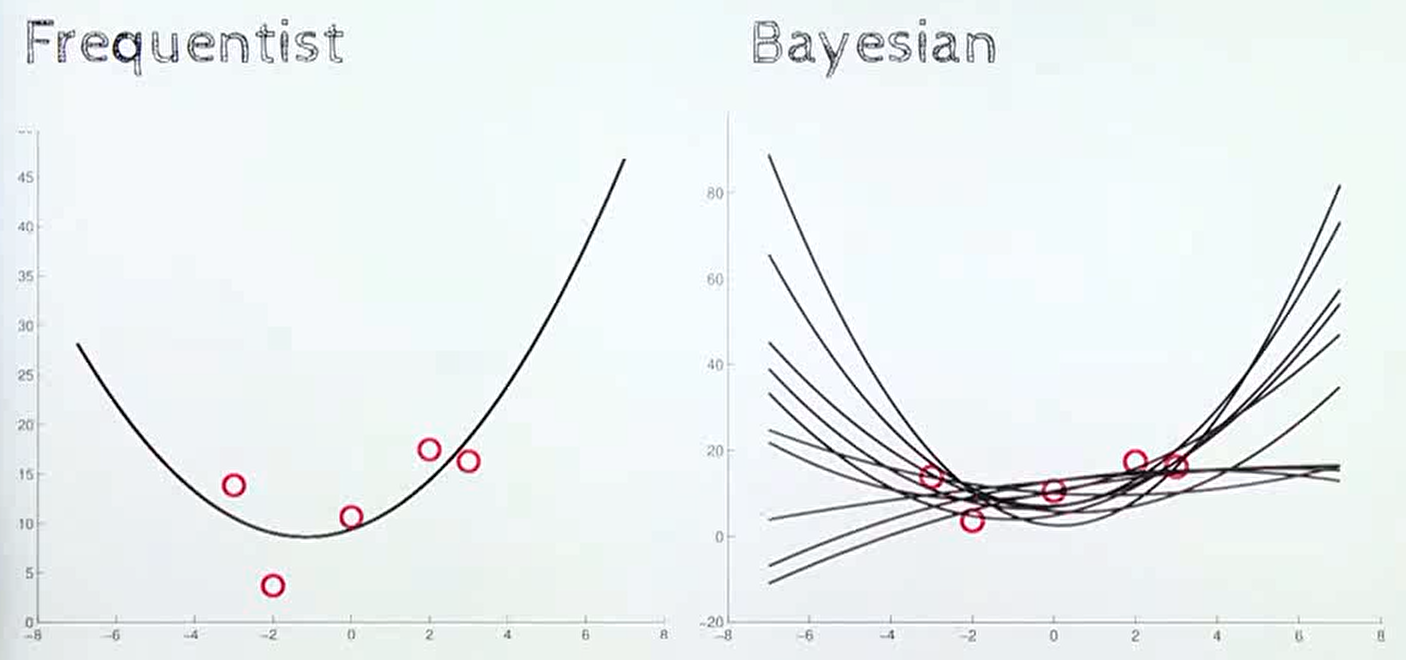
빈도주의 방법과 베이지안 방법의 차이는 위 그림과 같은 regression 문제에서도 확인할 수 있다.

빈도주의의 경우 주어진 데이터를 가장 잘 설명할 수 있는 곡선을 하나 추정하는 것을 목표로 하지만 베이지안에서는 예측 자체가 불확실한 값이기 때문에 여러가지 가능한 함수가 있다고 이해하게 된다.

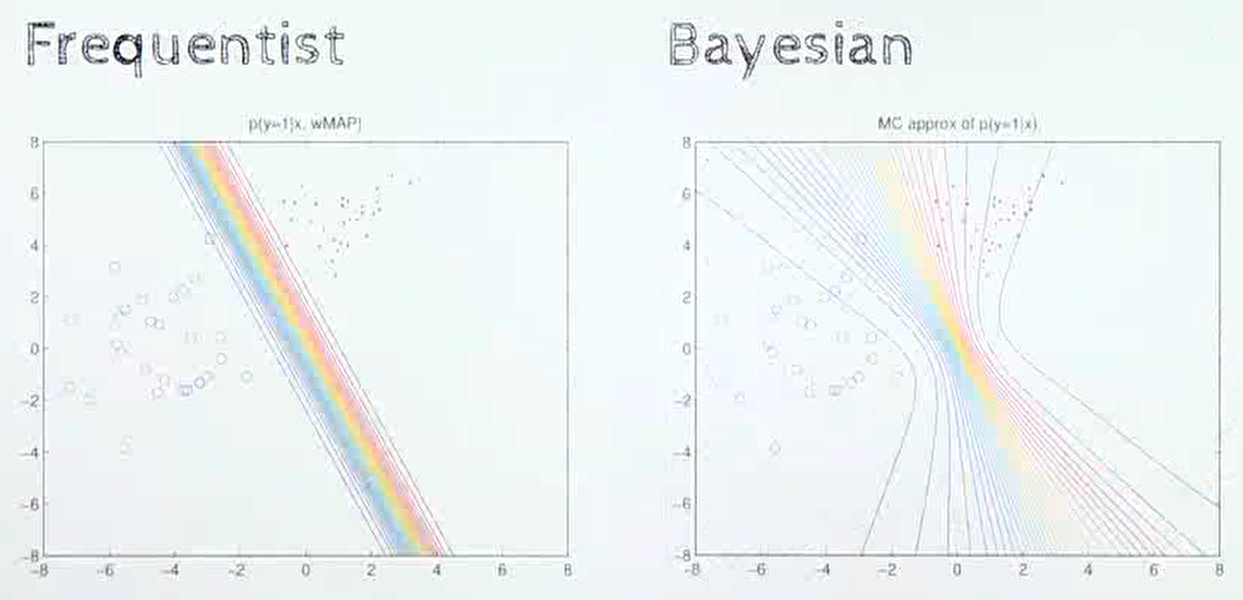
분류 문제를 풀 때도 빈도주의는 클래스를 분류하는 고정된 선을 이용하지만, 베이지안에서는 입력된 데이터에 따라 다양한 형태의 곡선을 나타낸다.

베이지안의 단점 & 베이지안 뉴럴 네트워크

베이지안 방법론은 불확실성을 정량화 할 수 있다는 장점이 있지만, posterior를 계산하기 위한 $p(D)$의 적분 계산이 불가능한 경우가 다수 발생한다.

기존의 머신러닝 방법에서는 한정된 파라미터 갯수로 인해 적분식을 그대로 계산하지 못하더라도 적분식의 결과를 근사화 하는 기법이 사용됐지만, 딥러닝과 같이 기하 급수적으로 파라미터가 많은 경우를 대상으로 적분 또는 근사화하는데 어려움이 있어 베이지안 뉴럴 네트워크 라는 개념이 도입됐다.

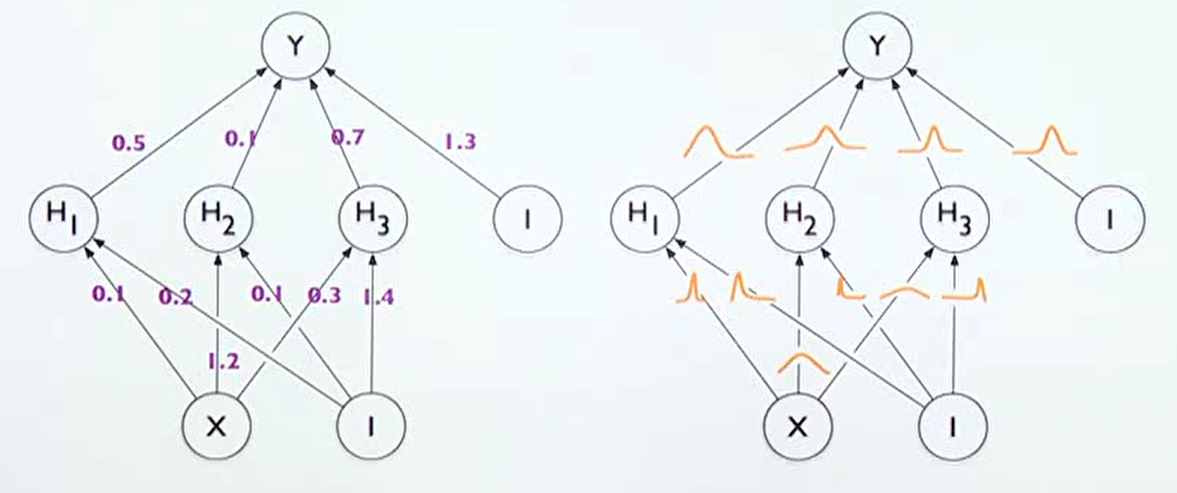
• 베이지안 뉴럴 네트워크는 위의 오른쪽 그림이다.

기존의 뉴럴 네트워크가 학습이 끝나면 weight가 고정된 값을 가졌지만, 베이지안 뉴럴 네트워크는 각 weight 또한 불확실성을 가지는 확률 분포로 나타나 진다는 점에서 차이가 있다.

각 weight가 불확실성을 가지는 확률 분포이므로 최종 출력인 Y 또한 불확실성을 가지는 확률 분포를 가지게 된다.

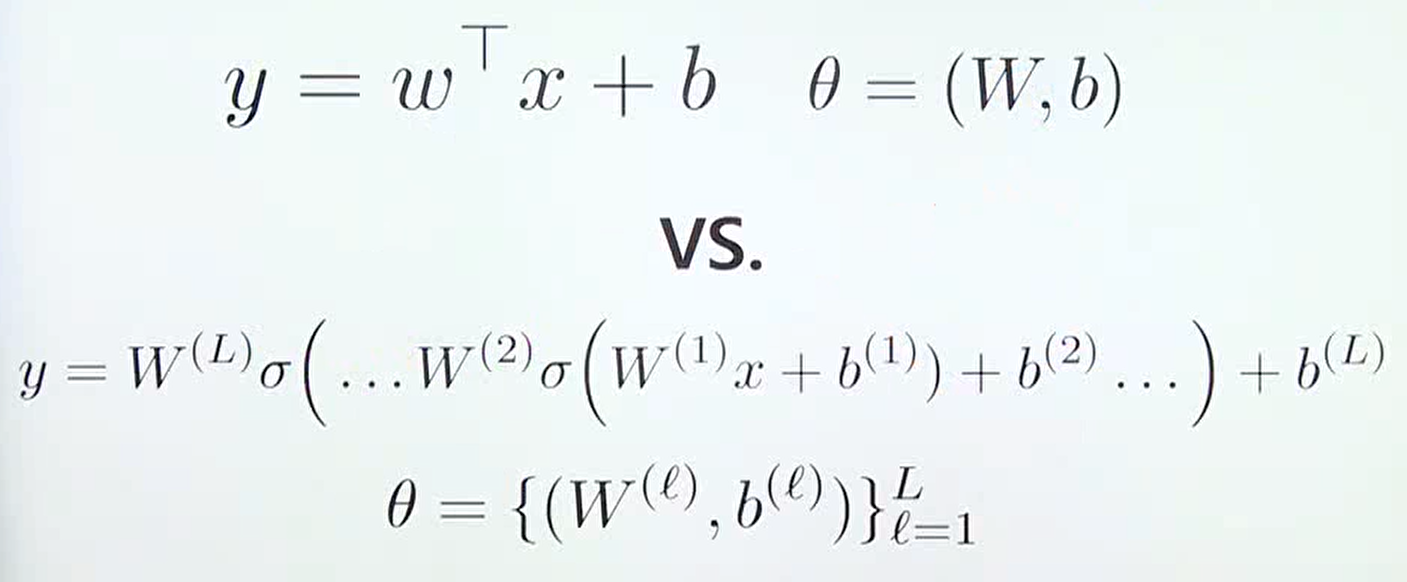
위 식은 선형 함수와 딥러닝 모델이 갖는 기본적인 개념은 같다는 것을 의미한다.

베이지안 뉴럴 네트워크의 관점에서는 모든 $\theta$값인 모든 $W,b$에 대하여 prior distribution을 가지고 어떻게 posterior distribution으로 업데이트 할 것인지를 다룬다고 말할 수 있다.

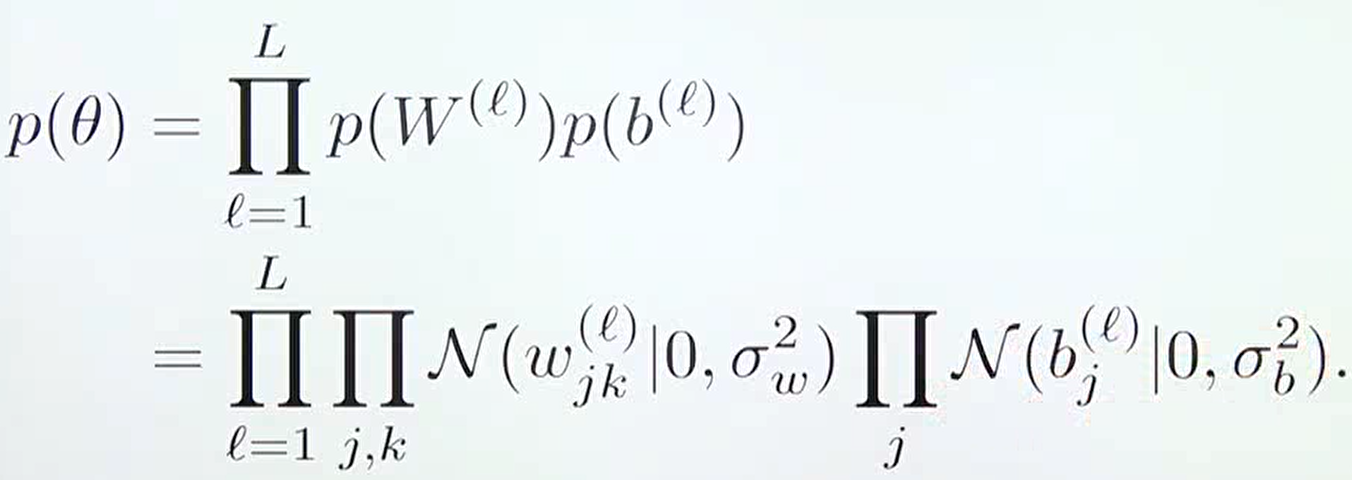
보통 딥러닝에서 사용하는 사전 확률 분포(prior)는 가우시안 분포를 따른다고 가정하며, 위 식과 같은 형태를 가진다. 흔히 사용하는 Xavier, He initialization 또한 정규 분포 형태를 가지므로 위 식과 유사한 형태를 가지게 된다.

따라서 베이지안 뉴럴 네트워크의 베이지안 추론은 다음과 같이 파라미터의 posterior distribution을 계산한다.

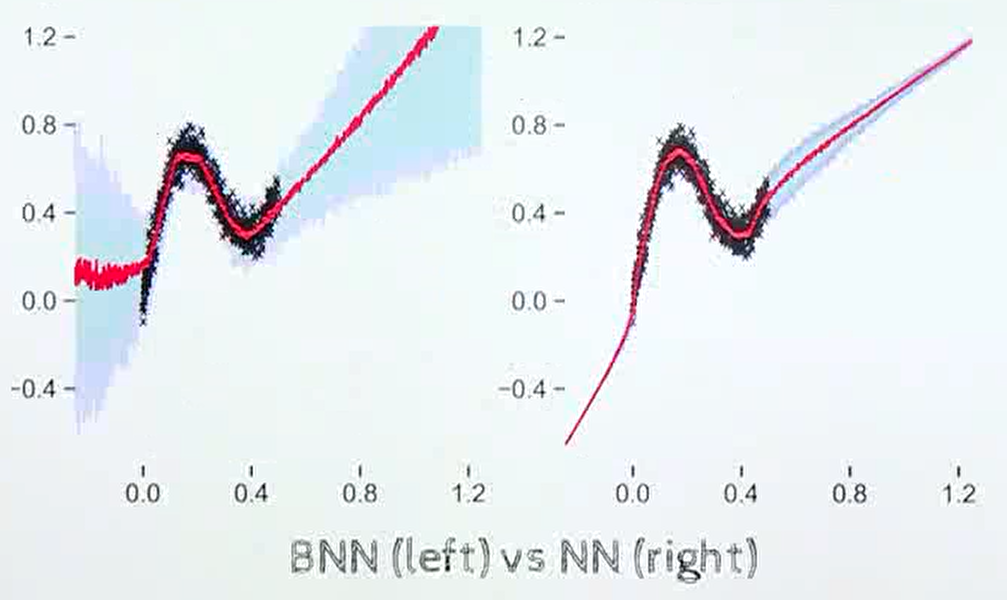
두 뉴럴 네트워크의 결과를 보면 왼쪽은 베이지안 뉴럴 네트워크이고, 오른쪽은 일반적인 뉴럴 네트워크이다.

검은색 점이 실제 학습 데이터가 입력된 구간에 해당하며, 빨간색 선은 뉴럴 네트워크의 출력에 해당한다. 빨간색 선 주위의 음영은 불확실성을 나타낸다.

베이지안 뉴럴 네트워크의 경우 데이터가 없는 구간의 경우 불확실성이 크게 나타나지만 뉴럴 네트워크의 경우 학습데이터가 없는 구간에도 불확실성이 낮다는 점을 확인할 수 있다.

---

하지만 앞에서 언급한 바와 같이 `posterior distribution`을 정확하게 계산할 수 없다는 문제가 있다.

이 문제를 해결하기 위해 다양한 방법이 있으며 대표적으로는 variational inference방법을 사용하는 것과 MonteCarlo Dropout을 사용하는 방법이 있다.

variational inference는 posterior distribution인 $p(\theta|D)$를 $q(\theta)$와 같은 방법으로 근사화 하는 방법을 의미한다. 이 때, $q(\theta)$는 접근하기 쉬운 정규 분포와 같은 확률 분포를 사용한다.

variational inference를 사용하면 완벽한 근사화는 아니지만 원래 posterior distribution이 가지는 특징을 잘 capture할 수 있도록 근사화 할 수 있다.

이후 montecarlo dropout과 active learning 등 다른 다양한 정보에 대해서는 밑의 블로그를 참고하자!

참고

https://gaussian37.github.io/dl-concept-bayesian_neural_network/