CDF & PDF

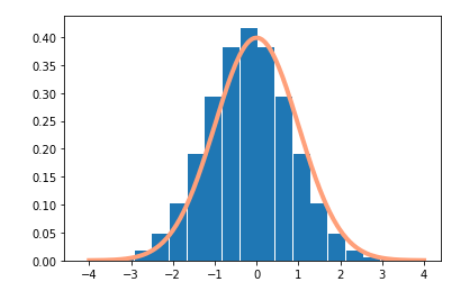
Random Variable

확률 변수(random variable)는 표본 공간의 각 표본에 대해 실수 값을 할당하는 함수이다. 쉽게 말해, 확률 변수는 실험이나 상황에 대해 숫자로 나타내는 것.

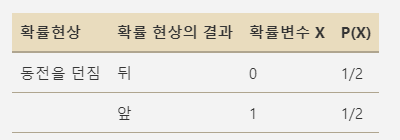
예를 들어, 동전 던지기 실험에서 앞면이 나오면 1, 뒷면이 나오면 0과 같이 할당할 수 있다.

그리고 이건 다시 2가지로 나뉜다.

• discrete RV
• continuous RV

동전은 말 그대로 discrete RV이여서 쉽게 생각할 수 있지만,

물 1L 한 병을 채우는데 얼만큼 나눠서 한번에 얼만큼 쏟으며 채울 수 있는지는 floating하기 때문에 discrete 하게 채울 수 없다.

CDF

Cumulative Distribution Function, 즉 누적 확률 분포(영어랑 한국어 해석이랑 다른데... 흠..)는 위의 개념에서 부터 시작한다.

위의 물 1L를 채우는 것을 구분하기 위해 특정 구간 구간을 나눠서 1L의 1/10만큼씩은 2/10L만큼 채우고 다음 1/10의 구간에는 1/10L 만큼 채워나가는 것을 의미한다.

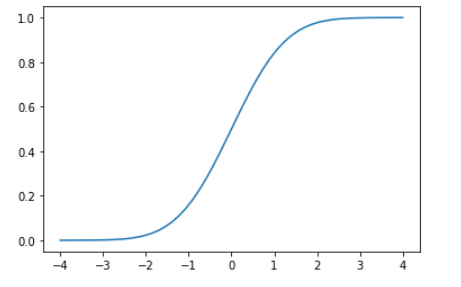
결구 처음 아무 시도도 없을 때는 반드시 그 확률이 0이지만 조금씩 채워 나가다 보면 그 끝은 하나를 다 채우는 1이 되는 것을 의미하고 이를 수식으로 다음과 같이 표현한다.

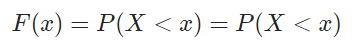
그런데 위 수식에서 $P(X<x)$가 뭔지 잘 이해가 안됐었는데.. GPT 선생님이 답해주셨다..

---

확률 변수 $P(X)$가 $x$ 보다 작은 값을 가질 확률인 $P(X<x)$에 대한 간단한 예시를 들어보겠습니다.

예시: 동전 던지기

가정: 동전을 던질 때, 앞면이 나올 확률이
$P(X = "앞면") = 0.5$ 이고, 뒷면이 나올 확률이
$P(X = "뒷면") = 0.5$ 라고 합시다.

여기서 확률 변수 $X$는 동전 던지기의 결과를 나타냅니다.

$X$가 앞면인 경우를 1로, 뒷면인 경우를 0으로 정의하겠습니다.

$P(X<1)$: 확률 변수 $X$가 1보다 작은 값을 가질 확률입니다. 즉, 앞면이 나올 확률을 나타냅니다. 위에서 앞면이 나올 확률은 0.5로 가정했으므로, $P(X<1)=0.5$입니다.

$P(X<0)$: 확률 변수 $X$가 0보다 작은 값을 가질 확률입니다. 0 미만의 값은 가능하지 않으므로, $P(X<0)=0$입니다.

---

PDF

문제는 위의 누적확률 분포로는 어느 구간에서 얼만큼의 양이 들어갔는지 모른다는 점이다. 이를 해결하기 위해 각 구간에 대해 미분을 하는 것이 확률 분포(Probability Desnsity Function)이다.

수식적으로는 다음과 같이 표현하며

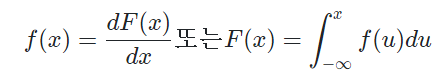
모든 구간에서의 적분을 하면 기존 1L의 1이 나와야 한다.

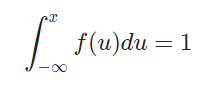
헷갈릴 수 있는 것은 f(x)의(확률밀도함수) y축은 기존 F(x)의 기울기 값이기 때문에 0이상의 양수에 대해 모두 허용한다. (0 <= f(x) <1 아님, 0<f(x) 임)

참고

• https://velog.io/@groovallstar/%ED%99%95%EB%A5%A0-%EB%B6%84%ED%8F%AC-%ED%95%A8%EC%88%98%EC%99%80-%ED%99%95%EB%A5%A0-%EB%B0%80%EB%8F%84-%ED%95%A8%EC%88%98%EC%9D%98-%EC%9D%98%EB%AF%B8