선형독립(일차독립) vs 기저
선형 독립이란?
Rm의 원소인 제로벡터⎝⎜⎜⎛0⋮0⎠⎟⎟⎞에 대하여c1⎝⎜⎜⎛a1⋮an⎠⎟⎟⎞+c2⎝⎜⎜⎛a1⋮an⎠⎟⎟⎞+...+cn⎝⎜⎜⎛a1⋮an⎠⎟⎟⎞을 만족하는 상수가
ci=⎝⎜⎜⎛0⋮0⎠⎟⎟⎞일 경우 선형독립(Linearly Independent)라 한다.
반대로
ci=⎝⎜⎜⎛0⋮n⎠⎟⎟⎞에 0이 아닌 상수가 있을 경우 선형종속(Linearly Dependent)라고 한다.
Example)
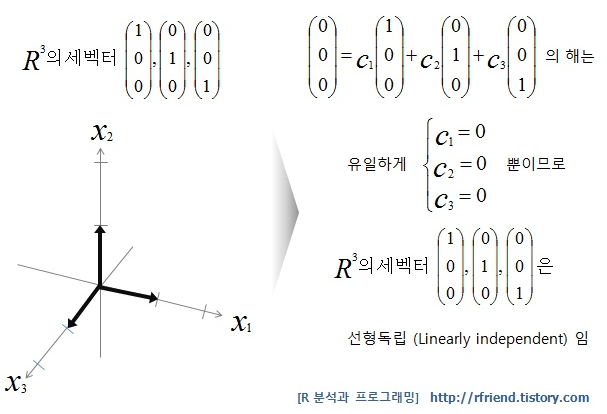
R3의 원소인⎝⎜⎛000⎠⎟⎞=c1⎝⎜⎛100⎠⎟⎞+c2⎝⎜⎛010⎠⎟⎞+c3⎝⎜⎛001⎠⎟⎞의 경우⎝⎜⎛c1=0c2=0c3=0⎠⎟⎞이 유일하므로 선형독립
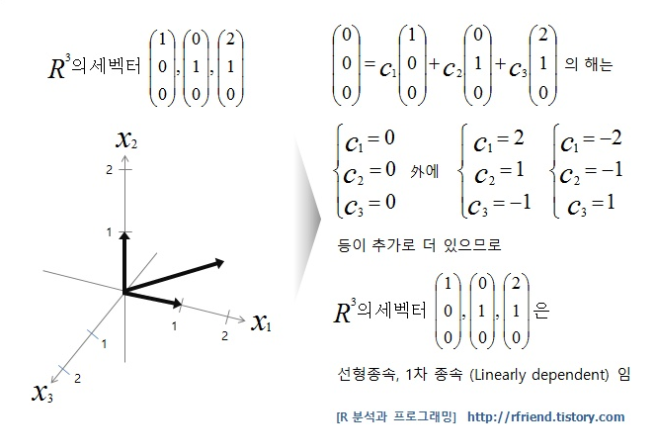
기저란?
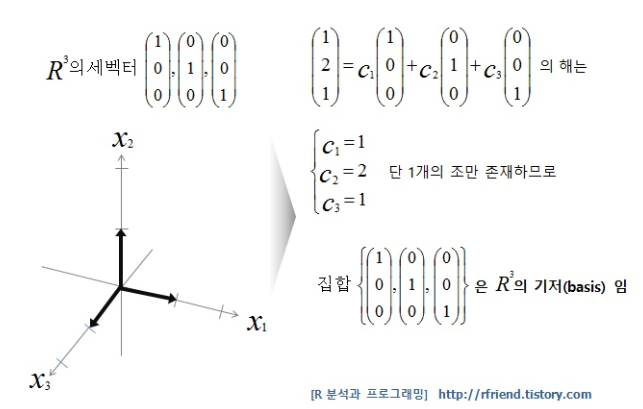
어떤 벡터 공간 V의 벡터들이 선형독립이면서 벡터 공간 V 전체를 생성할 수 있는 벡터 집합의 임의의 원소를 표현 하기 위해 필요한 최소한의 벡터로 이루어진 집합
Rm의원소인벡터⎝⎜⎜⎛1⋮n⎠⎟⎟⎞에대하여c1⎝⎜⎜⎛a1⋮an⎠⎟⎟⎞+c2⎝⎜⎜⎛a1⋮an⎠⎟⎟⎞+...+cn⎝⎜⎜⎛a1⋮an⎠⎟⎟⎞을 만족하는 상수가
ci=⎝⎜⎜⎛a1⋮an⎠⎟⎟⎞단 하나일 경우 기저라 한다.
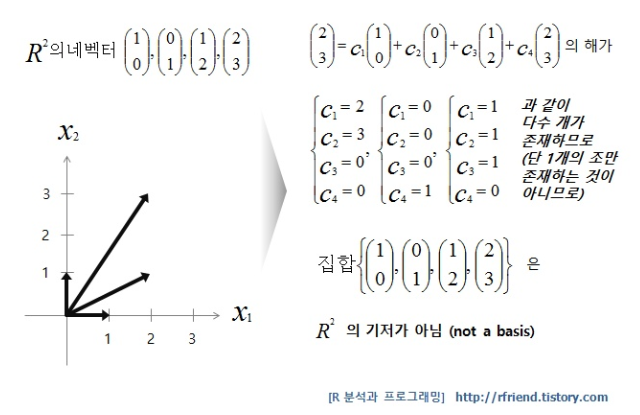
선형독립 vs 기저)
R3의 원소인 벡터가 ⎝⎜⎛000⎠⎟⎞이냐 혹은⎝⎜⎛121⎠⎟⎞과 같은 0이 아닌 원소로 이루어졌는가?
글로하면 어렵다..
그냥 내 방식대로 이해하면
선형 종속(일차 종속)의 경우 어떤 값을 아무리 스칼라 곱을 해서 늘리고 줄이고 지지고 볶고 해도 어떤 벡터와 겹쳐져 특정 공간을 만들 수 없게 될 수 있다.
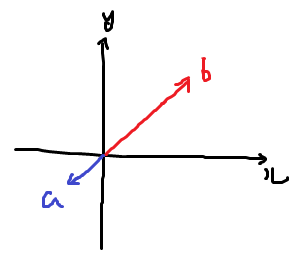
그래서 반드시 어떤 스칼라 곱을 하더라도 다른 벡터와 동일해질 수 없는 0만이 유일한 벡터만 있어야 하고 이를 선형 독립(일차 독립)이라 한다.
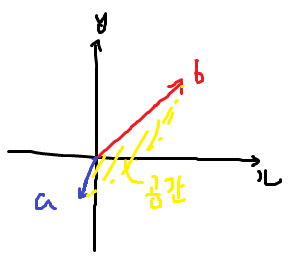
이걸 최소로 만들어주는 스칼라들의 집합인 벡터 집합을 기저(basis)라고 함
(스칼라들의 집합 이라한 건 [c1,c2]를 의미함)
이렇게 선형 독립을 이용하면 차원 축소에서도 유용하게 쓰일 수 있다.
(공간을 만들 수 있는 집합들을 기반으로 차원을 줄이는 것이니까 데이터가 보존됨)
<참고
https://blog.naver.com/uoonm1/222328233470 >






