Norm (노름) 이라고 읽는단다..
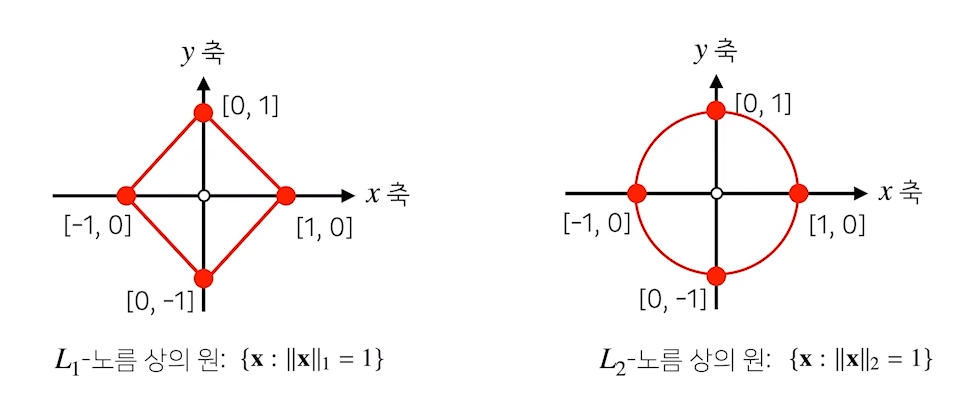
- L1 norm은 각 성분의 변화량을 절대값을 모두 더하면 된다..
- L2 norm은 유클리드 거리로써 좌표평면 위에서 원점에서의 거리라고 생각하면 된다..
수식은 알겠는데 왜 다른 norm을 쓰고 언제 쓰는거지?
기본적으로 norm은 두 벡터 사이의 거리 혹은 각도를 구하는데 사용한다 (각도는 L2 norm만 가능!)
각도를 구하려면 L2 norm에 제2Cos법칙을 쓰면 된다!
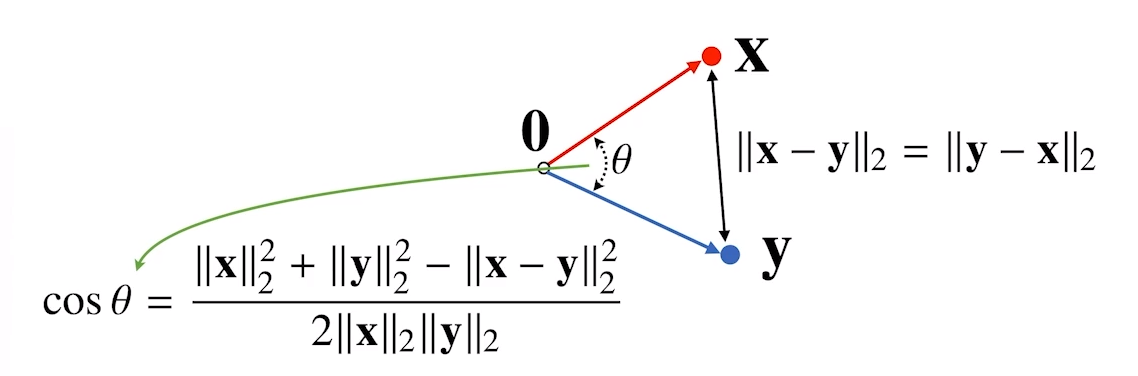
근데 분자를 계산하기 너무 귀찮고 복잡하니 이걸 해결해주기 위해 내적(Inner Product)를 사용하자!
L1 norm은 계산값에 절댓값을 취하고, L2 norm은 계산값에 제곱을 취한다.
L1 norm은 이상치에 robust하지만, L2 norm은 이상치에 민감하게 된다.
L2 norm에 대한 간단한 예시를 들면
수식: || f(xi) - f(xj) ||^2
예를 들어,
xi = [1, 2, 3]이고 xj = [4, 5, 6]이라고 가정하자. 두 벡터 간의 거리의 제곱을 계산하면
f(xi) = [1, 4, 9]
f(xj) = [16, 25, 36]
먼저 f(xi) - f(xj)를 계산:
[1 - 16, 4 - 25, 9 - 36] = [-15, -21, -27]
이제 이 벡터의 각 원소를 제곱:
[-15^2, -21^2, -27^2] = [225, 441, 729]
마지막으로 각 원소를 더한 결과:
225 + 441 + 729 = 1395
따라서 주어진 예시에서 || f(xi) - f(xj) ||^2 = 1395가 된다.Numpy에서의 내적!
내적은 원래 두 행렬의 곱을 의미한다
일반적으로 수학에서 말하는 두 행렬의 곱은 i행렬의 n번째 행벡터 * j행렬의 m번째 열 벡터를 의미하지만
numpy에서 사용하는 내적 함수인 inner()는 일반적인 수학과는 조금 다르다..
numpy에서 사용하는 내적 함수인 inner()는 XYT를 의미한다!!
즉! numpy에서의 inner()는 X와 Y의 행의 갯수가 같아야 한다!!
