VAE

💡 VAE란 무엇인가?

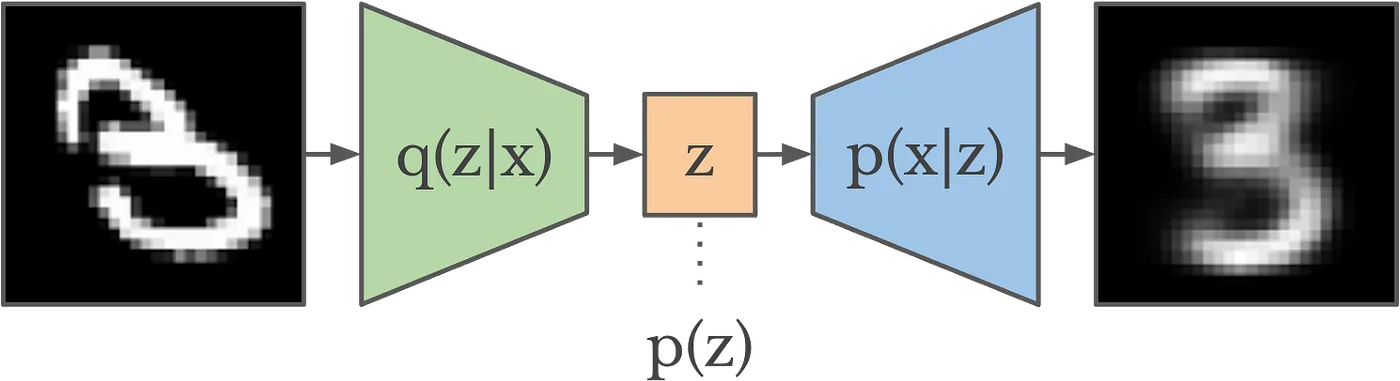
Variational Autoencoder(VAE)는 입력 데이터의 변형을 생성하는 데 사용되는 생성 모델로 일반적인 오토인코더와 마찬가지로 인코더와 디코더로 구성되어 있습니다.

하지만 VAE는 잠재 공간(latent space)을 연속적이고 확률적인 방식으로 모델링하여 원본 입력을 정확히 재구성할 뿐만 아니라 원본과 유사한 새로운 데이터를 생성할 수 있습니다.

💡 잠재 공간(Latent Space)

잠재 공간은 입력 데이터의 중요한 특성을 압축하여 표현하는 저차원 공간입니다.

예를 들어, 28x28 픽셀의 흑백 이미지 (MNIST 데이터셋)는 784차원의 벡터로 표현되지만 실제로 의미 있는 정보는 그보다 훨씩 적은 차원에 존재합니다.

VAE는 이러한 유의미한 정보를 잠재 공간에 효과적으로 압축하여 표현합니다.

💡 VAE와 일반 오토인코더의 차이점

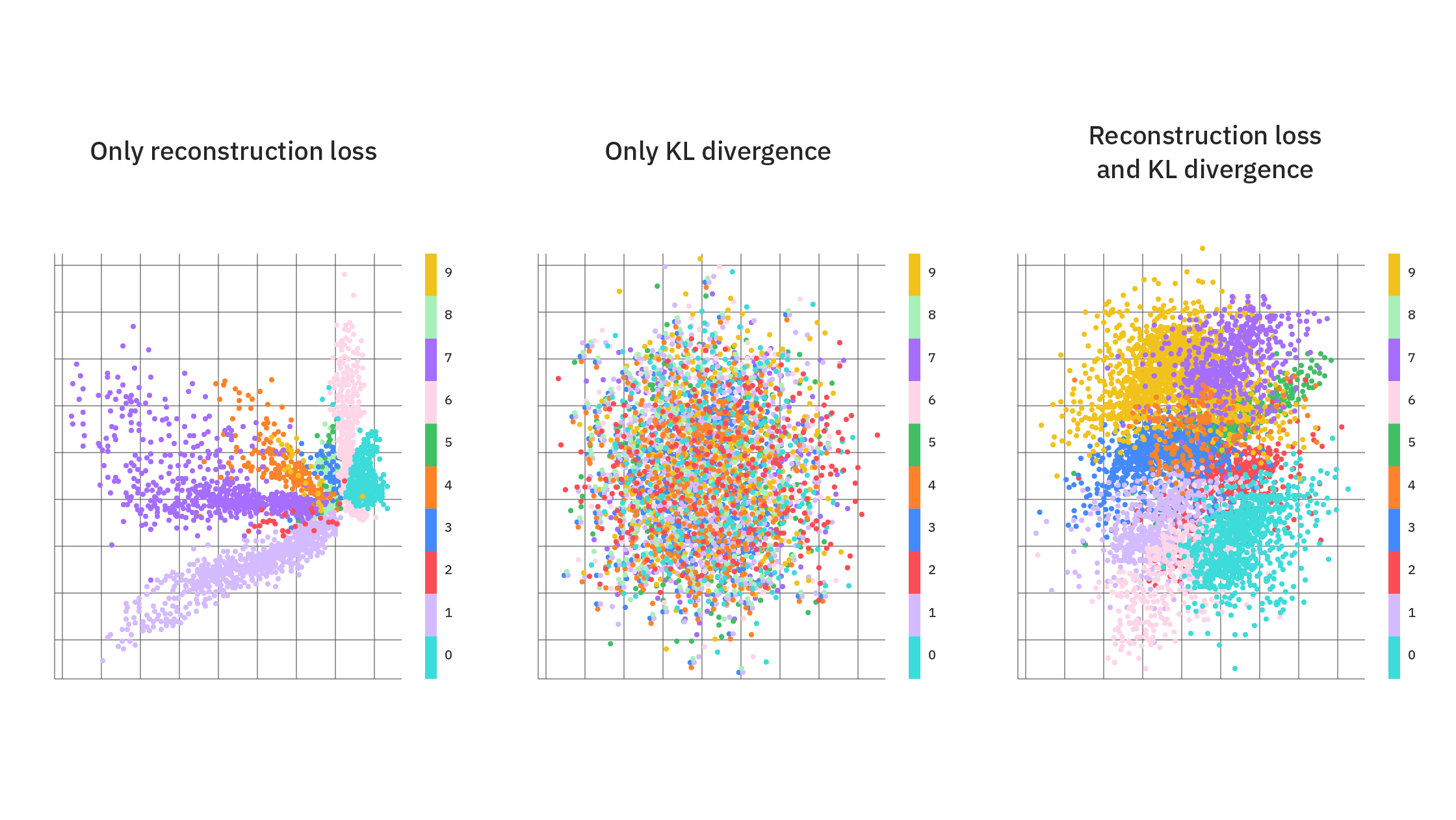
일반 오토인코더는 입력 데이터를 압축하고 재구성하는 데 중점을 두며 잠재 공간을 고정된 벡터로 표현합니다.

반면 VAE는 잠재 공간을 확률 분포로 모델링하여 새로운 데이터를 생성할 수 있는 능력을 갖추고 있습니다.

또한 VAE는 재구성 손실 외에도 Kullback-Leibler(KL) 발산을 손실 함수에 포함시켜 잠재 공간의 분포가 사전에 정의된 분포와 유사하도록 학습합니다.

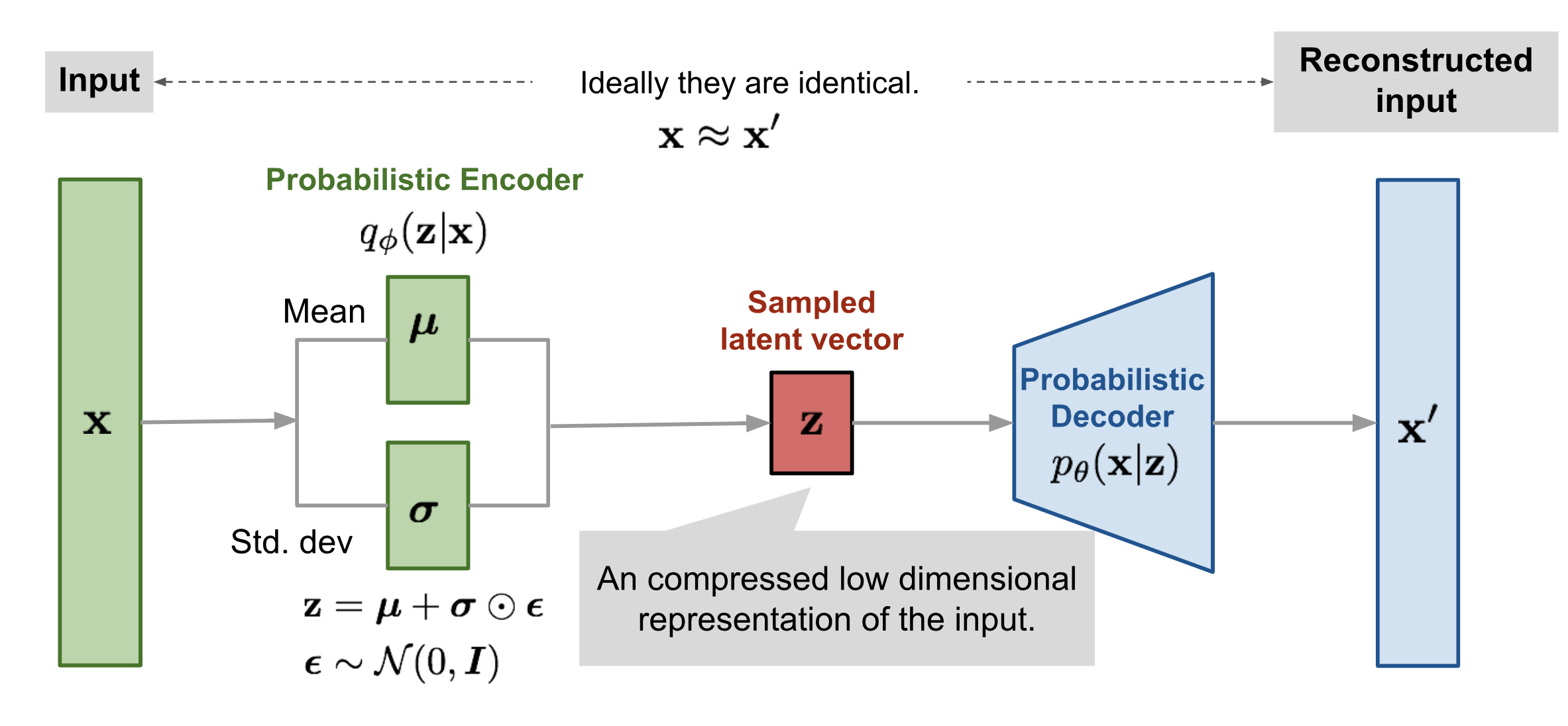
💡 Reparameterization Trick

VAE는 잠재 공간에서 샘플링을 통해 데이터를 생성하지만 이 과정은 미분 가능하지 않음 문제가 발생합니다.

이를 해결하기 위해 Reparameterization Trick을 사용해 샘플링 과정을 미분 가능하게 만들어 모델의 학습이 가능하도록 합니다.

💡 수식 분석

1️⃣ 잠재 변수 모델에서의 추론

관측된 데이터 $x$와 잠재 변수 $z$를 가지는 확률 모델 $p(x, z)$를 고려합니다.

우리의 목표
주어진 $x$에 대한 잠재 변수의 사후 분포 $p(z|x)$를 추정하는 것

발생하는 문제

$p(z|x) = \frac{p(x, z)}{p(x)} = \frac{p(x, z)}{\int p(x, z) \, dz}$
이 사후 분포는 분모의 적분 계산이 어려워 직접 계산이 불가능함

2️⃣ 변분 추론 : 근사 분포 $q(z)$ 도입

사후 분포 $p(z|x)$를 직접 계산하는 대신 이를 근사하기 위해 $q(z)$라는 변분 분포를 도입함

이때 $q(z)$는 $p(z|x)$와 유사하도록 선택돼야 하며 두 분포간의 유사성은 Kullback-Leibler(KL) 발산으로 측정됨

$D_{KL}(q(z) \| p(z|x)) = \int q(z) \log \frac{q(z)}{p(z|x)} \, dz$

KL 발산을 최소화하는 것은 $q(z)$가 $p(z|x)$에 가까워지도록 함

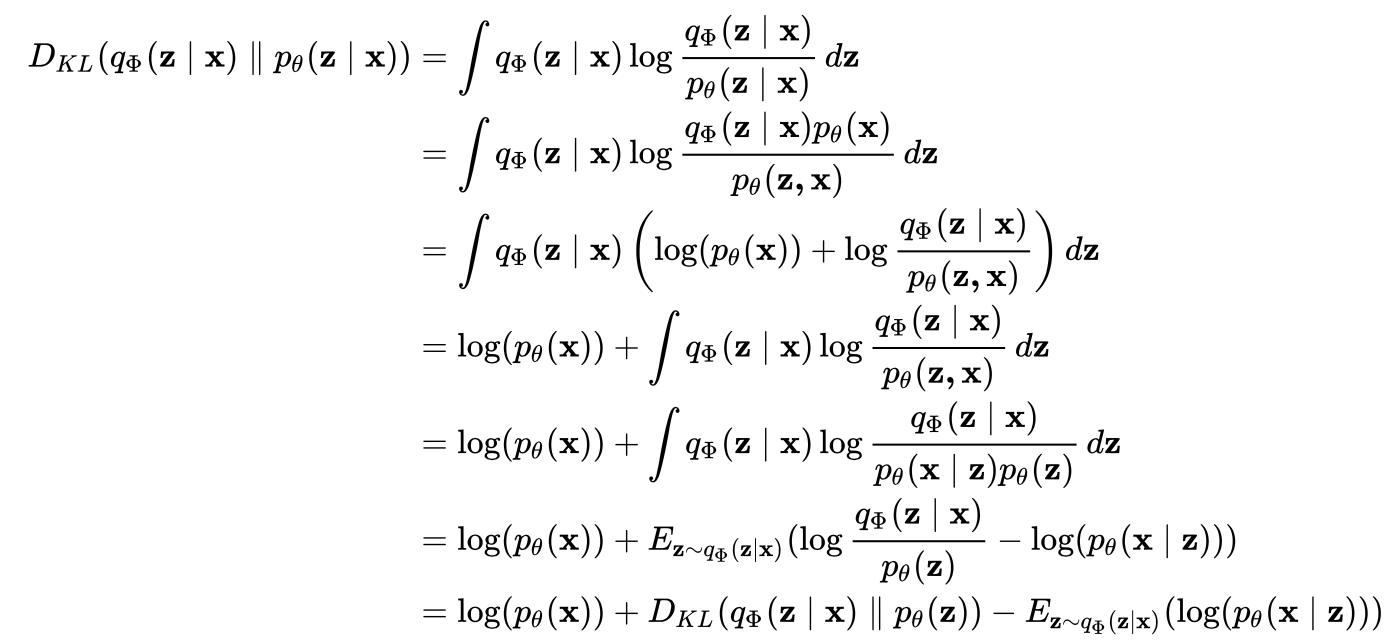
3️⃣ ELBO 유도 : Jensen의 부등식 활용

$\log p(x) = \log \int p(x, z) \, dz = \log \int q(z) \frac{p(x, z)}{q(z)} \, dz$

여기서 Jensen의 부등식을 적용하면

$\log p(x) \geq \int q(z) \log \frac{p(x, z)}{q(z)} \, dz = \mathbb{E}_{q(z)}\left[\log \frac{p(x, z)}{q(z)}\right]$

이 우변이 바로 ELBO(Evidence Lower Bound)입니다.

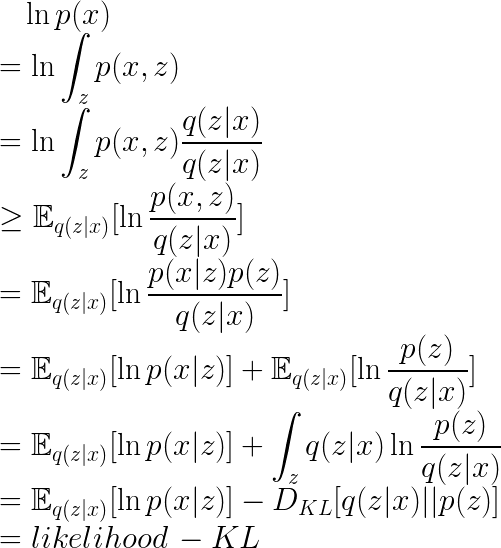
4️⃣ ELBO의 대안적 표현

ELBO는 다음과 같이 재구성 손실과 정규화 항으로 분해될 수 있습니다.

$\mathbb{E}{q(z)}[\log p(x|z)] - D{KL}(q(z) \| p(z))$

첫 번째 항: 재구성 손실, 잠재 변수 $z$로부터 원래 데이터 $x$를 얼마나 잘 복원하는지

두 번째 항: 정규화 항, 근사 분포 $q(z)$가 사전 분포 $p(z)$와 얼마나 유사한지 측정

5️⃣ ELBO와 증거 $log\ p(x)$의 관계

ELBO는 $log\ p(x)$의 하한이며 그 차이는 KL 발산으로 표현됨

$\log p(x) = \text{ELBO} + D_{KL}(q(z) \| p(z|x))$

따라서 ELBO를 최대화하는 것은 KL 발산을 최소화하는 것과 동등하며 이는 $q(z)$가 $p(z|x)$에 가까워지도록 함

💡 VAE의 활용 분야

VAE는 이미지 생성 외에도 다양한 인공지능 분야에서 활용됩니다.

예를 들어 이상 탐지, 노이즈 제거, 데이터 압축, 신약 개발 등에서 사용되며 복잡한 데이터의 잠재 구조를 학습하고 새로운 데이터를 생성하는 데 강력한 도구로 자리 잡고 있습니다.