[CS224W] CH2. Traditional Methods for ML in Graphs

Review

머신러닝 과제 ⇒ node-level, link-level, graph-level

랜덤포레스트, SVM과 같은 머신러닝 모델을 훈련시킨 후 새로운 노드/링크/그래프가 주어졌을 때 그것의 feature를 뽑아 Y라는 예측을 수행할 수 있도록 함.

좋은 모델 성능을 위해서는 그래프에 대한 효과적인 feature design이 가장 중요! ⇒ node, link, graph 각각 나누어서 살펴볼 예정.

ML in Graphs

Goal: Make predictions for a set of objects

Design choices:

• Features: d-dimensional vectors
• Objects: Nodes, edges, sets of nodes, entire graphs
• Objective function: What task are we aiming to solve?

Undirected graphs에 대해서만 다룰 예정.

Node-Level Tasks and Features

Goal: 네트워크에서 노드의 구조와 위치를 특정시키는 것

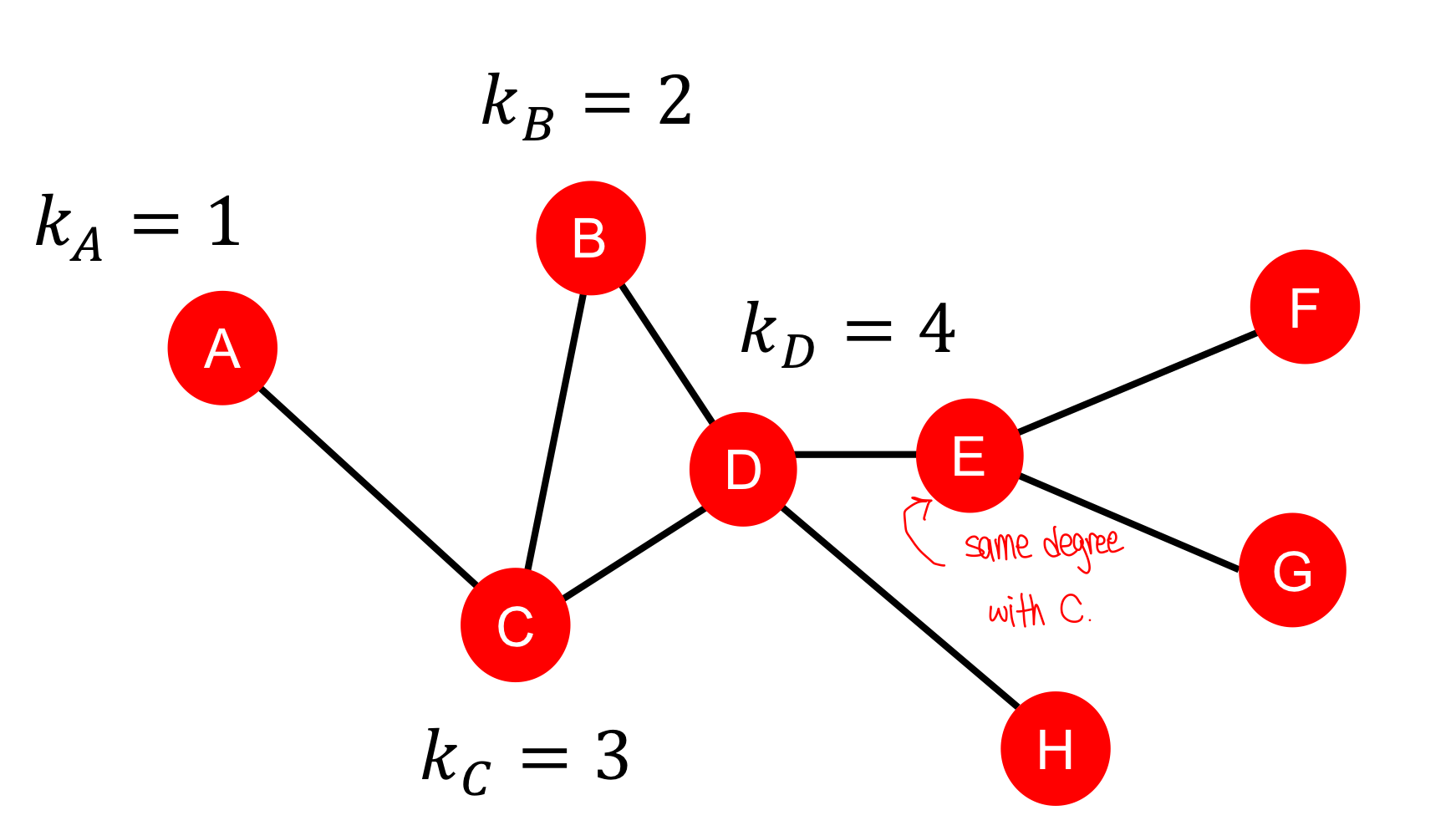
1. Node degree

$k_v$: 노드 v가 가지고 있는 엣지의 개수(neighboring nodes). 모든 근처 노드들을 동일한 가중치로 생각.

2. Node centrality

Node degree는 노드의 중요성을 고려하지 않고 이웃 노드들의 개수만 파악함.

Node centrality $c_v$는 그래프에서의 노드 중요성을 고려한 지표이다.

1. Eigenvector centrality

노드 v의 centrality는 주변 노드들의 centrality의 총합이다. ($\lambda$는 정규화를 위한 상수) 주변 이웃이 중요할수록 나도 더 중요해진다는 논리.

재귀적인 식을 가진 기본 형태를 행렬 형태로 표현하기.

• A = 인접 행렬(Adjacency matrix). $A_{uv} = 1$ if $u\in N(v)$
• c = Centrality vector
• $\lambda$ = 고윳값(Eigenvalue)

centrality vector c가 A의 고유벡터임을 확인할 수 있음. 가장 큰 고윳값 $\lambda_{max}$는 항상 양수이고 유일하다. (by Perron-Frobenius Theorem)

고윳값 $\lambda_{max}$에 대응하는 $c_{max}$가 centrality score에 사용된다.

2. Betweenness centrality

다른 노드들 사이에 가장 짧은 경로에 포함되어 있는 노드가 중요하다는 논리.

• $c_A = c_B = c_E = 0$

• $c_C = 3$ (A-C-B, A-C-D, A-C-D-E)

• $c_D = 3$ (A-C-D-E, B-D-E, C-D-E)

중요한 커넥터의 역할.

3. Closeness centrality

다른 모든 노드들 각각의 shortest path가 짧으면 중요하다는 논리.

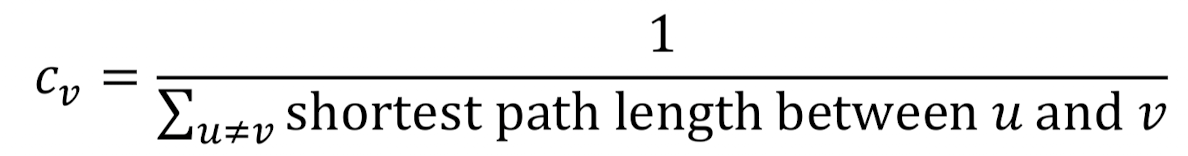
<2번과 같은 예시로 적용>

• $c_A = 1 / (2+1+2+3) = 1/8$
  (A-C-B, A-C, A-C-D, A-C-D-E)
• $c_D = 1/(2+1+1+1) = 1/5$
  (D-C-A, D-B, D-C, D-E)

3. Clustering coefficient(결집 계수)

해당하는 노드 v의 이웃 노드들이 서로 어떻게 연결되어 있는지 보여주는 지표.

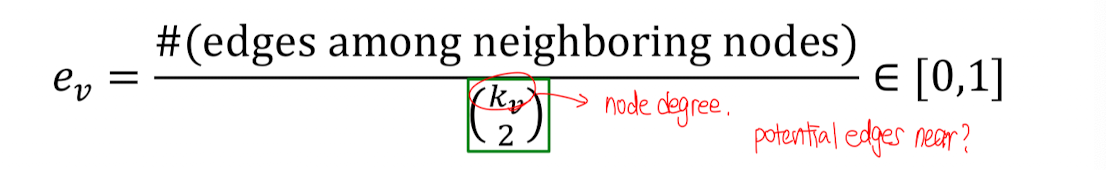
#($k_v$개의 주변 노드들 중 노드의 pair 개수) 아래 예시에서는 6개가 됨 (4C2)

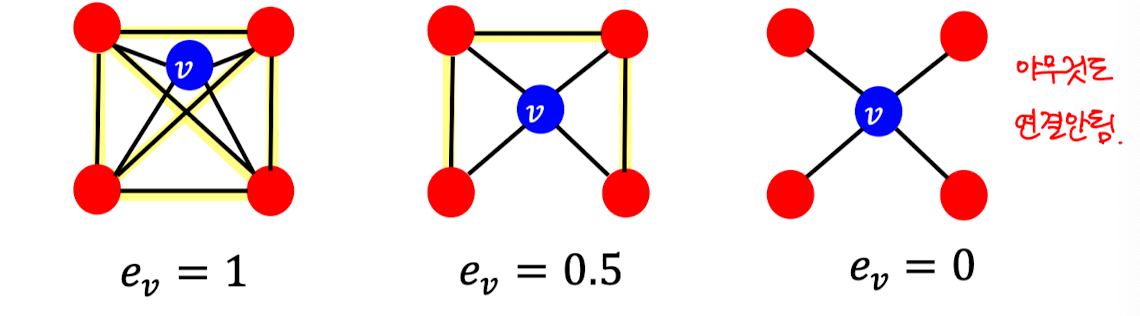
Clustering coefficient는 ego-network(node degree가 1인 네트워크)에 있는 삼각형의 개수를 센다. $e_v = 0.5$ 예시의 경우 6개의 삼각형 중 3개가 있는 걸 볼 수 있음.

삼각형 개수 counting을 graphlet(=pre-specified subgraphs) counting으로 일반화할 수 있음.

4. Graphlets

목표: 노드 u를 둘러싼 네트워크 구조를 설명하는 것 = Graphlet

• Degree: #(해당 노드와 맞닿는 엣지 개수)
• Clustering coefficient: #(해당 노드와 맞닿는 삼각형 개수)
• Graphlet Degree Vector(GDV): #(해당 노드와 맞닿는 graphlet의 개수)

💡 Graphlets: Rooted connected induced non-isomorphic subgraphs
Induced subgraph: 해당 부분집합에서 모든 노드가 엣지로 연결되어 있는 부분그래프
Graph Isomorphism: 노드의 ordering 차이로 인해 다르게 표현되지만 완전히 같은 구조를 가지는 그래프들.

** Two graphs which contain the same number of nodes connected in the same way ⇒ be isomorphic (동형성)

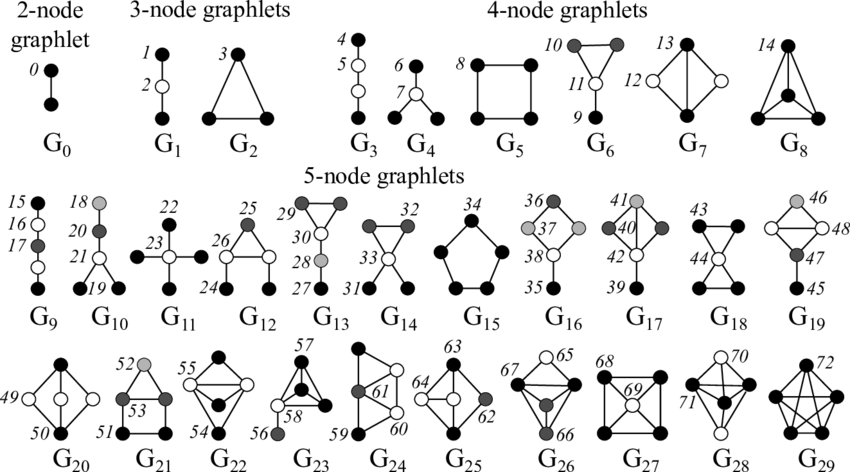
• 하나의 graphlet이라 하더라도 어느 노드에 위치하느냐에 따라 다르게 넘버링.
• G6의 경우 10번 옆에 있는 건 isomorphic하기 때문에 번호가 없음.
• Graphlet ID: Root, “position” of node u
• 5개의 노드까지는 73개의 각각 다른 graphlet이 있다.

Graphlet degree vector(GDV): 73개의 축을 가진 벡터(graphlet 사이즈가 2~5일 때). 노드의 이웃의 topology에 대한 정보를 제공해준다. node degrees나 clustering coefficient보다 국지적인 네트워크 구조 유사성(Local topological similarity)에 대해 상세한 척도가 되어준다.

Importance-based features	Structure-based features
Node degree	Node degree
Node centrality measures	Clustering coefficient
	Graphlet count vector(GDV)
그래프에서 영향력 있는 노드를 예측하는데 유용(social network에서 인플루언서 유저 예측)	그래프에서 노드가 수행하는 특정 역할을 예측하는데 유용 (단백질 상호작용 네트워크에서 단백질의 기능 예측)

---

Link Prediction Task and Features

Link-Level Prediction Task

기존에 있는 링크에 기반하여 새로운 링크가 있을지 없을지 예측하는 것이 목표. test할 때는 기존 링크 없이 노드의 쌍들이 rank되어 있고 top K개의 노드 쌍들이 연결된다고 예측한다.

💡 Key Point: 노드의 쌍을 위한 feature를 디자인하는 것.

Task 종류

1) Links missing at random: 링크를 랜덤으로 지운 후 그들을 예측하는 걸 목표로 함.

예시: 단백질 연결, 상호작용과 같이 시간의 흐름에 영향받지 않는 정적인 네트워크.

2) Links over time: 시간이 흐름에 따라 변하는 그래프.

$G[t_0, t'_0]$ 그래프가 주어졌을 때 $G[t_1, t'_1]$ 시간에 나타날 것으로 예측되는 랭킹이 매겨진 엣지 리스트 L을 결과로 내는 것. ($G[t_0, t'_0]$ 시간에는 없는 엣지들이어야 함)

예시: 물류 교통 네트워크, SNS, …

Evaluation

• $n = |E_{new}|$: test 시기 $[t_1, t'_1]$ 동안 나타나는 새로운 edge 개수
• L에서 top n개를 뽑고 그것이 올바른 edge들인지 count

🤔 Methodology: 각 노드의 쌍 (x,y)마다 점수를 계산 = c(x,y) ⇒ 내림차순으로 점수 배열 ⇒ top n개의 쌍을 새로운 링크로 예측 ⇒ 실제로 test 기간 동안 나타나는지 보기

Link-Level Features

1. Distance-Based Features

정의: 두 개의 노드 사이에 가장 짧은 경로의 거리

한계: 이웃 오버랩(neighborhood overlap)의 정도(연결의 강도)를 알 수 없음. (B,H)는 가장 짧은 경로가 2개나 있지만 (B,E)와 (A,B)는 경로가 1개밖에 없음.

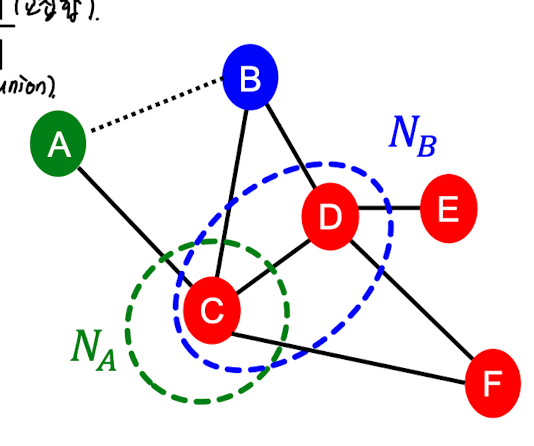
2. Local Neighborhood Overlap

정의: v1과 v2 노드 사이에 공유된 이웃 노드들의 개수.

• Common neighbors: $|N(v_1)\cap N(v_2)|$ 연결되어 있지 않은 두 노드들 간에 공통된 노드들이 공유된다면, 이 둘은 이후에 연결될 가능성이 높ㄷ다.
• Jaccard’s coefficient: $\frac{|N(v_1)\cap N(v_2)|}{|N(v_1)\cup N(v_2)|}$, common neighbors의 정규화된 버전.
• Adamic-Adar index: $\sum_{u\in N(v_1)\cap N(v_2)}\frac{1}{log(k_u)}$, social network에서 많이 사용됨. 노드 A와 B간에 공통되는 이웃들이 많다고 하더라도, 이웃들의 degree가 매우 크다면 이 둘이 연결될 가능성은 낮다고 평가.

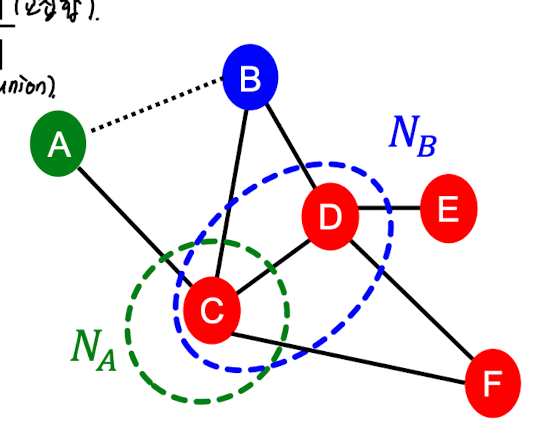
[예시 문제]
$N(A) = \{C\}, N(B) = \{C, D\}$
Common Neighbors = {C} = 1
Jaccard’s coefficient = |{C}| / |{C,D}| = 1/2
Adamic-Adar index = $\frac{1}{log(k_C)} = \frac{1}{log4}$

한계: 만약 두 개의 노드들이 공통된 이웃들이 없다면 metric 값은 항상 0. 그러나 아직 미래에 연결될 가능성이 존재한다. ⇒ Global neighborhood overlap이 그 문제를 해결

3. Global Neighborhood Overlap

Katz index: 주어진 노드의 쌍 사이에 모든 길이의 path의 빈도를 구함. 그래프 인접 행렬의 제곱(powers of the graph adjacency matrix)을 사용해서 Katz index를 계산.

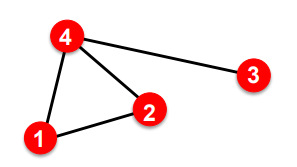
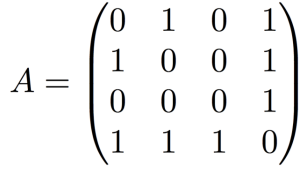
• 예시 그래프와 인접 행렬(Adjacency Matrix)

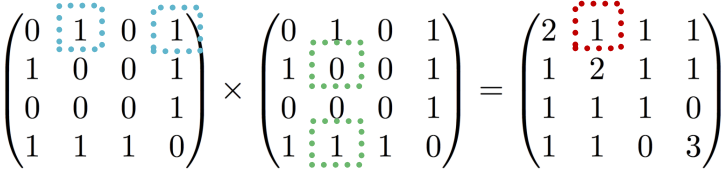
• 파란 사각형은 노드 1의 이웃
• 초록 사각형은 이 이웃으로부터 노드 2로 가는 length 2의 path.
• 이들을 각각 곱한 값이 빨간 사각형.
  ⇒ $A^2$의 (1,2) 성분 = 1.
  ** 실제로 길이가 2인 노드 1~2의 길은 (1, 4, 2)

베타: 더 긴 길이의 경로에 대해 적은 가중치를 두기 위한 discount factor

L 길이의 걸음 수에서 L을 무한대로 보내주면 모든 걸음의 거리를 구할 수 있음.

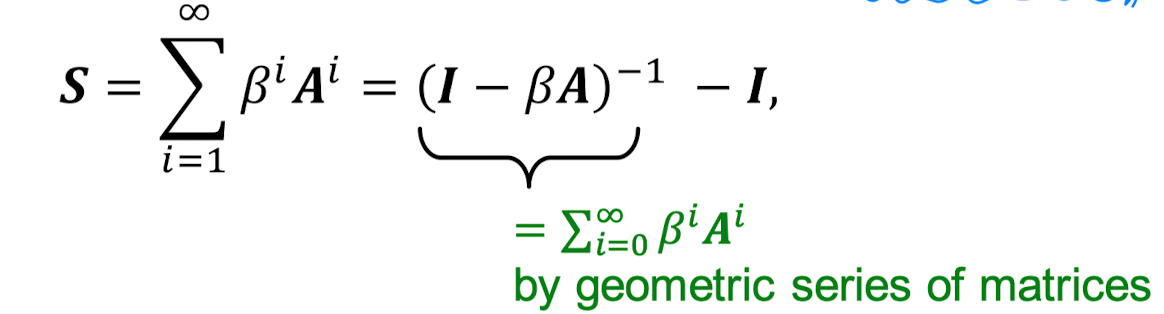
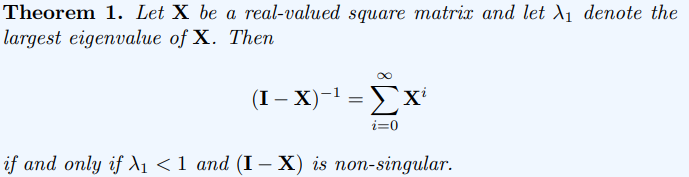
Theorem 1의 X 자리에 $\beta A$를 넣으면 우리가 원하는 Katz index식에 i = 0일 때의 값을 더하게 된 것. i = 0일때 $\beta A = I$ (identity matrix)이므로 다음과 같은 식이 나온다.

Graph-Level Features and Graph Kernels

Kernel Methods

그래프 수준 예측에서 전통적인 ML에 널리 쓰이는 방식. feature vectors 대신에 kernels를 디자인하자.

• Kernel $K(G, G') \in \mathbb{R}$(실수)은 데이터 사이의 유사성을 측정.
• Kernel Matrix $\bold{K} = (K(G, G'))_{G,G'}$ 은 항상 Positive semidefinite (= 양수 고유값을 가지고 있음)
• $K(G, G') = \phi(G)^T\phi(G')$ (dot product)
• 한 번 kernel이 정의되면 Kernel SVM과 같은 ML 모델로 예측할 수 있다.

Graph Kernels: 2개의 그래프 사이의 유사성을 측정

Goal: Design graph feature vector $\phi(G)$

Key Idea: Bag-of-Words (BOW) for a graph

• 문서에서 단어 개수를 셀 때 BOW를 사용 (순서 고려 안함)
• 노드들을 마치 단어로 취급해서 계산.
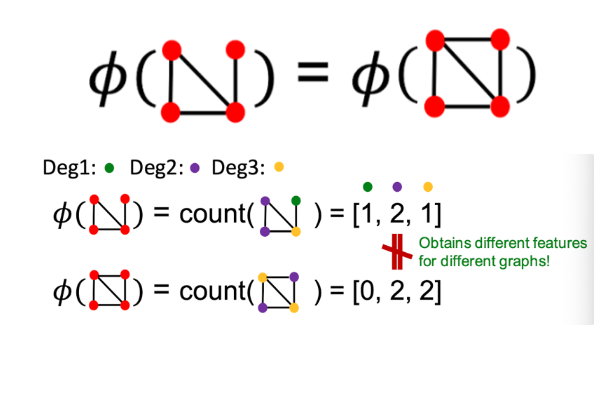
• 하지만 오른쪽 예시의 경우 둘 다 4개의 빨간 노드를 가지고 있기 때문에 다른 그래프이지만 똑같은 feature vector를 얻게 됨 (BOW로 계산한다면)
• Bag of node degrees로 계산한다면 다른 벡터가 나올 수 있음.

1. Graphlet Kernel (Bag of graphlets)

⇒ 그래프에 있는 다른 graphlet의 개수를 count

node level feature에서 배운 graphlet과는 다름!!

• 여기서는 모든 노드가 연결될 필요 X
• not rooted

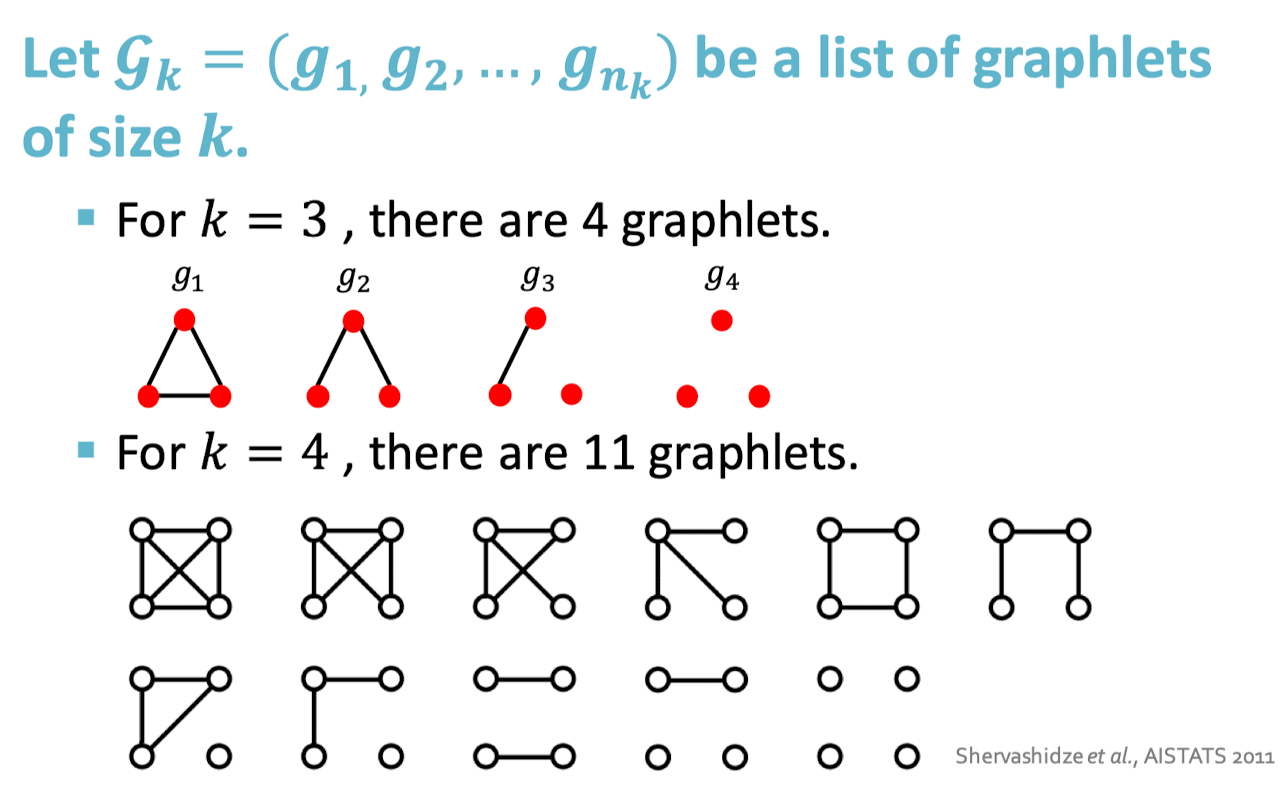
그래프 $G$와 graphlet list $G_k = (g_1, g_2, ..., g_{n_k})$가 주어졌을 때 graphlet count vector $f_G \in \mathbb{R}^{n_k}$를 다음과 같이 정의한다.

Graphlet Kernel for 2 graph G, G’ ⇒ $K(G, G') = {f_G}^Tf_{G'}$

• 문제: 만약에 두 그래프의 사이즈가 다르다면 값이 왜곡되어 나옴.
• 해결책: 각 feature vector를 정규화

한계: 계산량이 많다! (expensive)

• n 사이즈의 그래프 1개에서 k 사이즈의 graphlet을 세는 건 n의 k제곱만큼 시간이 걸림.
• subgraph isomorphism test(해당 그래프가 다른 그래프의 부분 그래프인지 확인하는 테스트)는 NP-hard(다항 시간 내에 풀 수 없는 문제)
• 그래프의 node degree가 d로 한정되어 있다면 graphlet을 세는 더 빠른 알고리즘이 존재함.

2. Weisfeiler-Lehman Kernel (Bag of colors)

좀 더 효율적인 graph feature descriptor $\phi(G)$를 디자인하자! ⇒ Color refinement

• Use neighborhood structure to iteratively enrich node vocabulary

그래프 G와 노드 집합 V가 주어졌을 때

1) 각 노드 v에 초기 색깔 $c^{(0)}(v)$를 지정

2) 반복적으로 노드 색깔을 재정의한다.

** 여기서 HASH는 다른 input을 다른 색깔로 매핑하게끔 하는 함수.

3) K번의 color refinement 이후에 나타나는 $c^{(k)}(v)$는 K-hop 이웃의 구조를 요약한다.

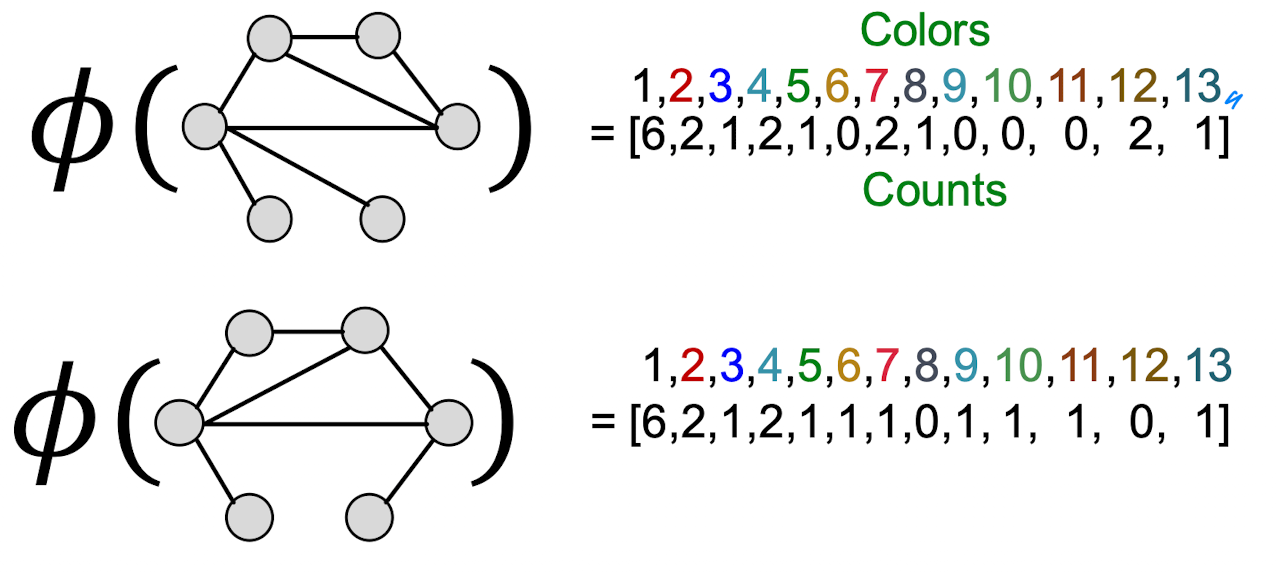
• computationally efficient: 각 스텝에서 color refinement하는 시간 복잡성이 엣지의 개수에 선형적이다. (=Hash function 계산이 단순하다)
• 커널 값을 계산할 때 2개의 그래프에 나타난 색깔들만 사용된다. 즉 노드의 총 개수가 색깔 종류의 개수이다.
• 색깔 counting 시간은 노드의 개수에 선형적으로 비례한다.
• Time complexity is linear in #(edges). ⇒ extremely fast