현재 연구들은 GNN의 세부적인 구조적 디자인을 제안하고 평가하는 데에만 초점을 둔다. 또한 GNN 디자인들은 주로 단일한 task에 전문화되어 있고 새로운 task 또는 데이터셋에 대해 최상의 GNN 디자인을 빠르게 찾는 방법에 대한 연구가 없다.

💡 논문 제안점 3가지

(1) 일반적인 GNN design space

(2) 유사도 메트릭이 포함된 GNN task space

(3) design space 평가 방법 → 많은 양의 모델-task 결합 중에서 인사이트를 끌어낼 수 있음.

1. Introduction

GCN, GraphSAGE, GAT를 포함한 많은 GNN 구조들이 개발되었고 많은 곳에서 이들이 적용되고 있다. (SNS, 화학, 생물학 등) 그러나 여러 이슈들이 나타나면서 GNN의 추후 발전을 막음.

[ISSUES]

• GNN 구조 디자인: design space보다 특정 GNN 디자인에만 초점을 두는 건 성공적인 GNN 모델 발견에 제한을 둔다.
  • GCN, GraphSAGE, GAT와 같은 모델들은 GNN design space의 특정 인스턴스들이다. GraphSAGE의 aggregation 함수를 summation으로 바꾸거나 skip connection 레이어를 추가한다면 이들은 GraphSAGE 모델이라고 불리지 않지만 특정 task에 대해서는 경험적으로 더 좋은 성능을 보일 수 있다.
• GNN 평가: 매번 등장하는 새로운 task들은 자연스럽게 기존에 존재하는 GNN 대표 task들과 비슷하지 않고, 어떻게 새로운 task에 알맞는 효율적인 GNN 구조를 디자인할지가 불명확하다.
• GNN 적용(시행): 그런 GNN design space를 넓게 탐색하는 걸 지원해주는 플랫폼(소프트웨어)이 부족하다.

[용어 설명]

GNN design space

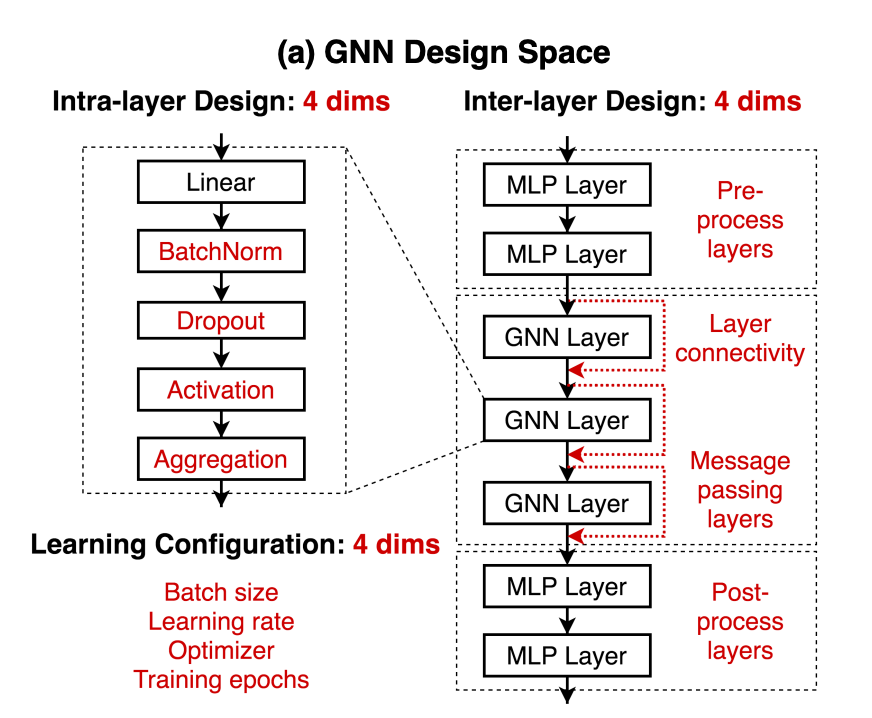
intra-layer design, inter-layer design, learning configuration을 포함하고 있는 일반적인 디자인 공간. GNN 모델 개발에 필요한 주요 구조 디자인 요소들을 포함하고 있다. 12개의 디자인 차원이 있고 315,000개의 디자인들을 만들 수 있다. design space를 제안하는 것뿐만 아니라 design space에 집중하는 것이 GNN 연구 발전에 어떻게 도움이 되는지를 보여줄 예정.

GNN task space

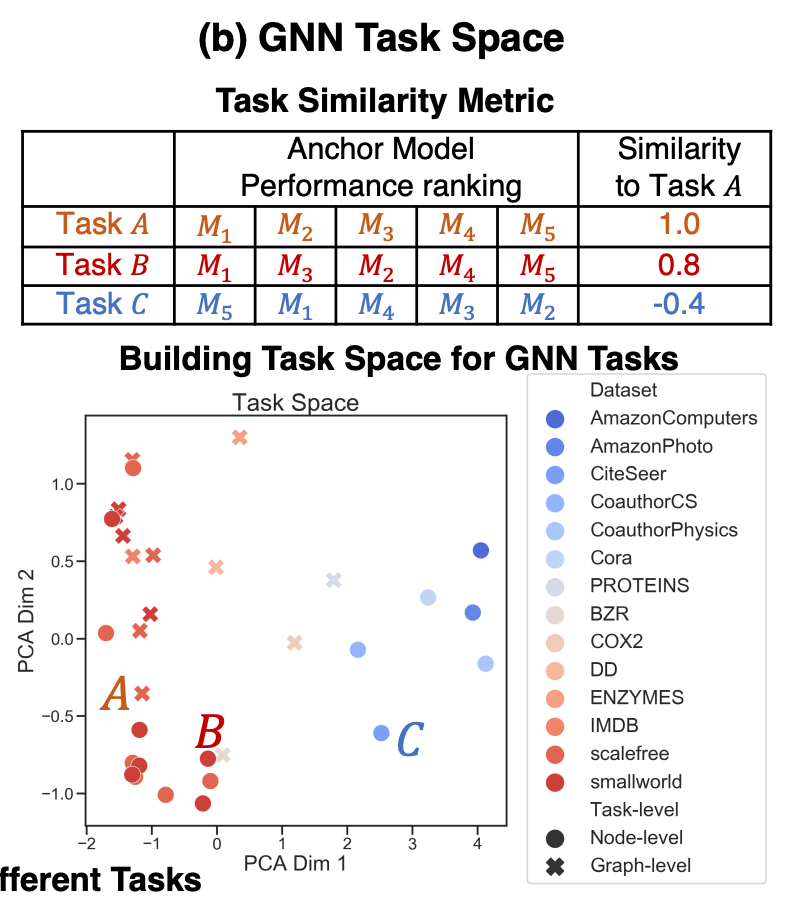
다른 task 간의 관계를 특정짓기 위해 task 유사도 평가지표를 제시하고 있다. 유사도는 두 task에 대해 GNN 구조의 고정된 집합에 포함된 디자인들을 적용하고 GNN 성능에 대해 Kendall rank correlation을 측정한다.

task 개수는 총 32개

• 12 synthetic 노드 분류 task, 8 synthetic 그래프 분류 task
• 6 real-world 노드 분류 task, 6 real-world 그래프 분류 task
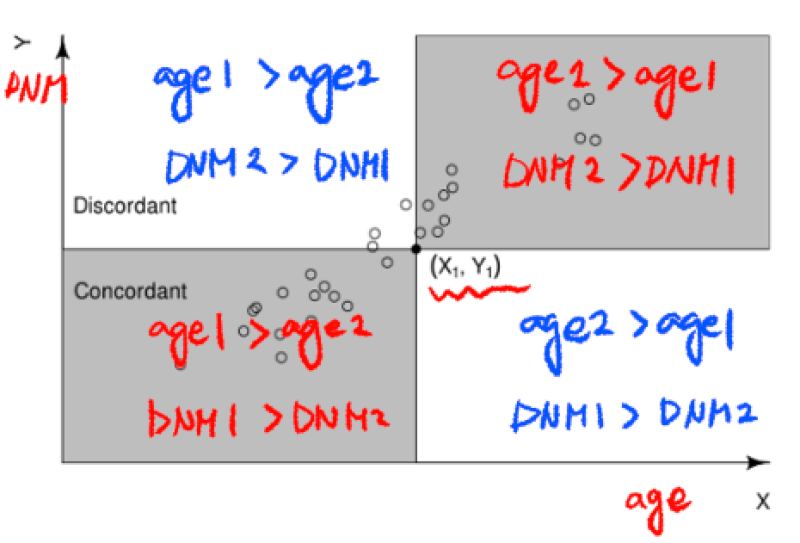
• Kendall rank correlation 설명
  • 1~1 사이의 값으로 순서를 기준으로 상관관계를 구함.
  • $\tau=\frac{\#concordant~ pairs-\#discordant~ pairs}{nC_2}$
  • concordant: 한 쌍의 요소들 모두 순서가 양수 또는 음수로 동일
  • discordant: 순서가 서로 반대
  • 

Design space evaluation

“배치 정규화가 일반적으로 GNN에서 도움이 되는가?”와 같은 인사이트를 얻는 것이 목표. 그러나 여기에서 정의한 design과 task space는 1000만개가 넘는 결합이 있기 때문에 GridSearch가 불가능하다. 따라서 controlled random search 평가 과정을 사용해서 각 디자인 차원 간의 trade-off를 효과적으로 이해할 수 있다.

결과적으로 이러한 연구를 통해 …

(1) 잘 작동하는 GNN을 디자인하는 데 쓰일 가이드라인을 제공한다.

(2) task들 간의 최상의 디자인을 전환할 수 있도록 도와준다.

• 굉장히 비슷한 GNN task에 대입할 모델을 찾기 위한 불필요한 알고리즘을 줄여줌.
• 새로운 GNN 디자인에 대한 영감을 주는 새로운 GNN task들을 찾을 수 있음.

(3) Open Graph Benchmark(OGB)에 있는 새로운 task/데이터셋에 대해 SOTA 성능을 보여준다.

이에 더해 하나의 GNN 구조 인스턴스에서 GNN 디자인 공간이라는 개념으로 확장시켜 GNN 구조 디자인에 대한 새로운 기회를 제공해줌.

2. Related Work

• 그래프 구조 탐색: 일반적인 GNN design space보단 각 GNN 레이어의 디자인에 집중하고, 적은 수의 노드 분류 task의 디자인들만 평가함
• GNN 모델 평가: GNN 모델 간의 fair comparison를 진행한 연구들이 있지만 마찬가지로 특정 GNN 디자인에 대해서만 고려함 (GCN, GAT, GraphSAGE)
• 다른 그래프 학습 모델: 본 논문은 좋은 성능과 여러 GNN task에 대한 효과적인 시행이 가능한 메시지 패싱 GNN에 포커스를 둠. 다른 대체 모델들의 design space들은 GNN들과 다르고 모듈화가 덜 되어 있다.
• 이동 가능한 구조 탐색: 컴퓨터 비전에서 주로 이동 가능한 구조 탐색에 대한 아이디어가 나왔고, 메타 레벨(본인 스스로를 설명하는 레벨)의 구조 디자인 또한 연구되고 있음. 이러한 접근들은 단일한 신경망 구조가 모든 task(다양성이 낮은 task들)에서 잘 작동한다는 가정이 필요한데 현재 매우 다양한 그래프 학습 task가 있는 상황에서는 그런 가정이 더이상 통하지 않는다.

3. Preliminaries

design: 구체적인 GNN 인스턴트 (ex. 5-layer GraphSAGE)
design dimensions: 각 디자인은 여러 개의 디자인 차원들에 의해 특성이 나타난다. (ex. 레이어 개수 $L \in \{2,4,6,8\}$, aggregation 함수 종류 $AGG\in \{max, mean, sum\}$)
design choice: 디자인 차원에서 선택한 실제 값
design space: 디자인 차원의 곱집합(Cartesian product) (ex. 레이어 개수 집합 L과 집계 함수 집합 AGG는 12개의 디자인이 가능하다)
task: task space를 구성하는 다양한 과제들 ex) Cora 데이터셋의 노드 분류 문제
experiment: task에 GNN 디자인을 적용하는 것
experiment space: 디자인과 task의 모든 결합을 거버함.

4. Proposed Design Space for GNNs

디자인 공간을 정의할 때 다음 원칙들을 사용한다.

(1) 가장 중요한 design dimensions를 사용할 것

(2) 최대한 적은 양의 design dimensions을 포함할 것 (ex. attention 모듈의 차원은 포함 X)

(3) 각 design dimension에서 일반적인(modest) 범위를 고려할 것

가장 광활한 디자인 공간을 제시하는 게 아니라 GNN 연구를 진행하는데 도움이 되는 디자인 공간에 어떻게 집중할 것인가를 제시하는 게 이 논문의 목표.

Intra-layer Design	Inter-layer Design	Training configurations
GNN layer 하나에 관한 것	여러 개의 레이어들이 신경망으로 구성될 때의 디자인	최적화 알고리즘 구성
Batch Normalization(True, False)	Layer connectivity(stack, skip-sum, skip-cat)	Batch size(16, 32, 64)
Dropout(False, 0.3, 0.6)	Pre-process layers(1,2,3)	Learning rate(0.1, 0.01, 0.001)
Activation(ReLU, PReLU, Swish)	Message passing layers(2,4,6,8)	Optimizer(SGD, Adam)
Aggregation(mean, max, sum)	Post-process layers(1,2,3)	Training epochs(100, 200, 400)

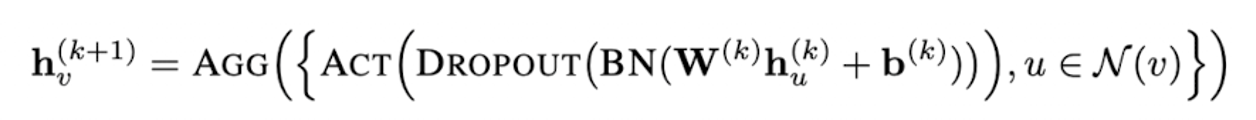
k번째 GNN 레이어 정의

Inter-layer Design 추가 설명

Skip-Connection: 이전 layer의 정보를 직접적으로 direct하게 이용하기 위해 이전 층의 입력(정보)를 연결한다.

• SKIP-SUM: residual connections. 이전 레이어의 결과를 나중 레이어의 결과에 직접적으로 더함. (Transformer에 있는 Residual Connection과 같은 개념)
• SKIP-CAT: dense connections. 이전 레이어의 결과를 나중 레이어의 결과에 concat을 진행.

GNN message passing layer 앞뒤로 MLP layer를 쌓을 수 있음 (Pre or Post process layers)

5. Proposed Task Space for GNNs

5.1 Quantitative Task Similarity Metric

기존 task 분류체계의 문제점

데이터셋 도메인(생물학, 소셜 네트워크), 또는 예측값 종류(노드, 그래프 분류)로 분류가 된다. 그러나 이러한 분류체계는 task/데이터셋 사이의 GNN 디자인 이동 가능성을 내포하고 있지 않다.

Task 유사도 평가 지수 (quantitative)

1. anchor model 선택

주어진 GNN task의 다른 요소들을 찾을 수 있는 다양한 GNN 디자인 집합을 찾는 것이 목표.

design space에서 D개의 랜덤한 GNN 디자인을 뽑는다.

⇒ 고정된 GNN task들의 집합에 디자인들을 적용하고 모든 task에 대한 각 GNN 모델의 평균 성능을 기록한다.

⇒ D개의 디자인들이 랭킹이 됐을 테고, M개의 그룹으로 슬라이스한 후 각 그룹에서 중앙값 성능을 가지는 모델들을 선택한다. ⇒ 최종 anchor model !

1. task 유사도 측정

주어진 2개의 task에 대해 M개의 anchor model들을 적용한 후 성능을 기록한다.

⇒ 모든 M개의 anchor 모델에 대해서 성능을 나열한다.

⇒ Kendall rank correlation(=task similarity)을 계산한다.

T개의 task들에 대한 것이라면 모든 task들에 대해 유사도를 측정한 후 나열하면 된다. 즉 T개의 task들을 비교할 때 필요한 계산량은 M * T개의 GNN 모델을 학습하고 평가하는 것과 같다.

일반적으로 M = 12로 두고 계산하면 디자인 공간에 있는 모든 디자인들에 대해 측정한 유사도와 근사한 값이 나온다.

5.2 Collecting Diverse GNN Tasks

제시된 디자인 공간과 task 유사도 평가지표를 제대로 평가하기 위해 다양한 synthetic 그리고 real-world GNN tasks/데이터셋을 32개 모았다. ⇒ medium-sized, diverse and realistic tasks 위주로

Synthetic tasks

인위적으로 만드는 데이터셋. 다양한 그래프 구조적 특성, features, labels를 고려해서 만듦.

• 그래프 통계량으로 측정되는 구조적 특성이 다양한 **small-world, scale-free graphs를 제작.
  • 좁은 세상(small-world) 네트워크: 무작위로 선택된 두 노드 사이의 일반적인 거리 L이 네트워크 노드 수 N에 로그에 비례하여 증가하는 네트워크. 몇 개의 무작위 연결만으로도 노드 간 연결거리가 현저히 줄어드는 네트워크. 낮은 C, 낮은 L
  • 척도 없는(scale-free) 네트워크: 정형화된 틀이 없다는 것. 무작위적(random)인 것과는 구분되는, 훨씬 생존성이 높은 네트워크. 성장하되 무작위가 아닌 선호에 따라 연결하는 경우 나타나는 네트워크. 평균 연결 이상으로 매우 많은 링크를 가진 노드 즉, 허브가 존재함.
    

• local 그래프 통계량: 평균 결집 계수(Average Clustering Coefficient C)
• global 그래프 통계량: 평균 최단 경로 길이(Average Path Length L)

$C\in [0.3,0.6],~ L\in[1.8,3.0]$ 사이의 값들로 그래프를 만드는데 이 범위로 8x8 그리드를 만들고 각 그리드 bin에 4개의 graph가 채우게끔 함. ⇒ 총 256개의 small-world, 256개의 scale-free 그래프가 만들어짐.

노드 특성의 경우에는 4가지 종류를 고려함: (1) 상수 스칼라 (2) 원핫 벡터 (3) 노드 결집 계수 (4) 노드 PageRank 점수

노드 레벨의 label의 경우 결집 계수와 PageRank 점수를 포함하고, 그래프 레벨의 label의 경우 평균 최단 경로 길이를 고려한다. 또한 feature와 label이 동일한 그래프끼리 묶인다면, 그 결합은 제외한다.

이를 모두 종합해서 12개의 노드 분류 문제와 8개의 그래프 분류 문제를 얻게 된다.

Real-world tasks

참고 논문에서 가져온 6개 노드 분류 문제들과 6개 그래프 분류 문제들을 사용한다.

6. Evaluation of GNN Design Space

Controlled random search

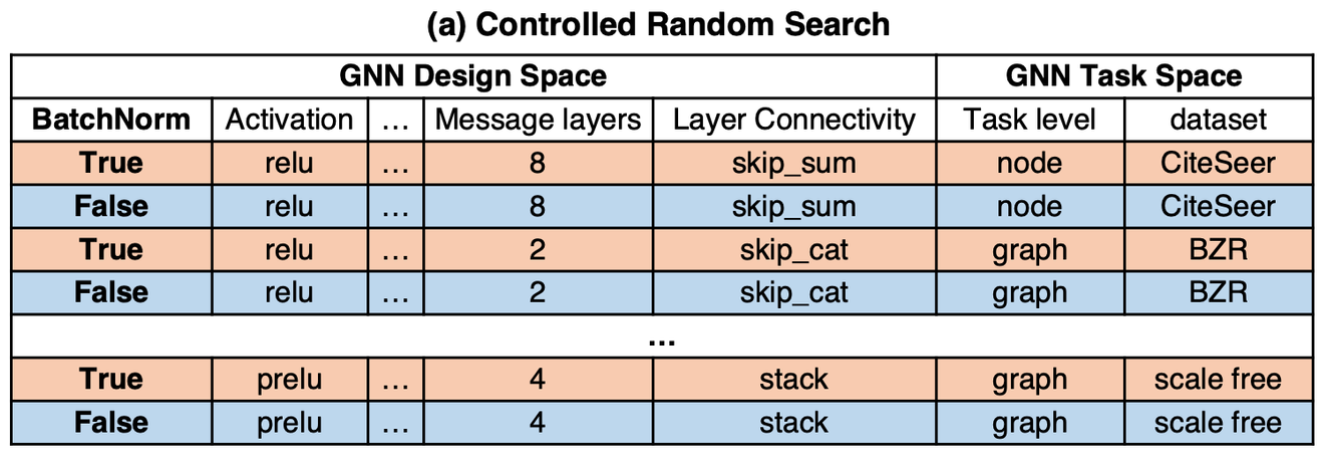
예시: BatchNorm(BN)을 추가하는 것이 GNN에 도움이 될까?

1. 10M개의 가능한 모델-task 결합들 중에서 모두 BN = True인 S개의 랜덤한 experiments를 추출한다. (S = 96으로 설정해서 각 task에 평균 3번 정도 적용해볼 수 있도록 함.)
2. 똑같은 설정에서 BN = False인 96개 experiments를 또 추출한다.

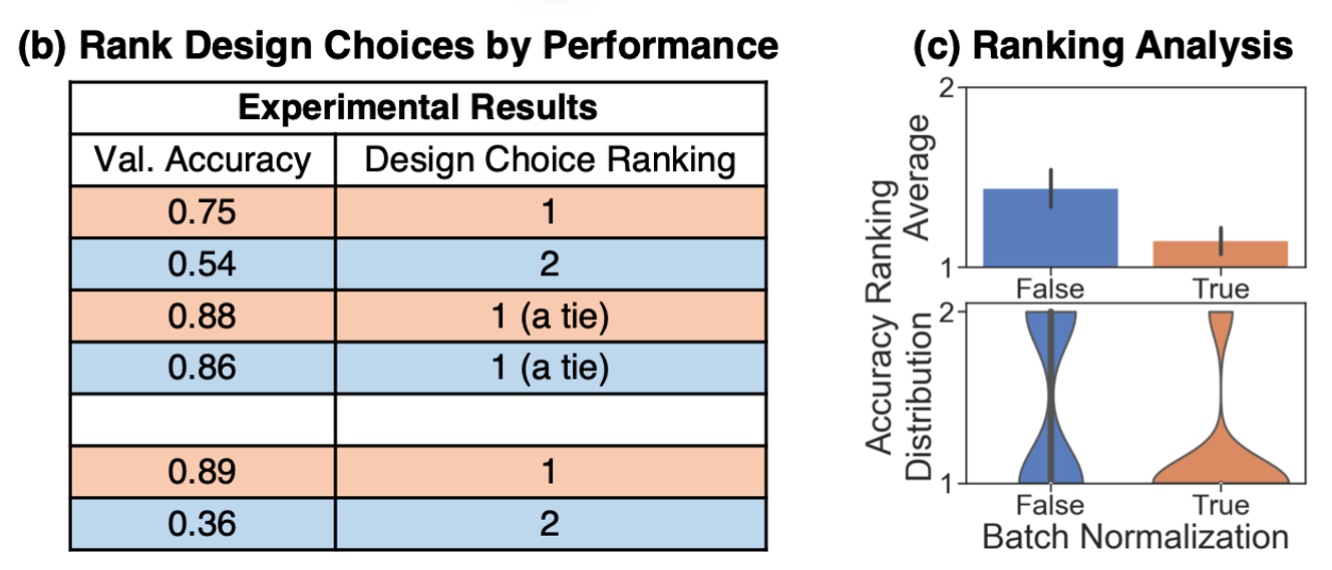
3. 나열된 결과의 robust함을 향상시키기 위해 tie(무승부)의 경우도 고려한다. (성능 차이가 0.02보다 작은 경우, 둘다 1로 rank)

BN = True이면 평균 1.15의 Rank를 가지고, BN = False이면 평균 1.44의 Rank를 가짐.

결론: BatchNorm(BN)을 추가하는 것이 GNN에 도움이 된다.

줄어든 계산량: 이 controlled random search는 full grid search에 비교했을 때 1000배 이상의 실험 수를 줄여준다. 모든 12개의 design choices에 대해 32개의 task를 돌리면 10 GPU로 5시간밖에 걸리지 않게 된다.

계산량 예산의 조절(Controlling the computational budget)

평가에 있어 모든 실험에서 GNN의 훈련 가능한 파라미터 수도 조정함. ⇒ pre-processing(&post-processing) layer 1개, message passing layers 3개, 은닉 차원 256개

7. Experiments

7.1 GraphGym: Platform for GNN Design

• GNN 시행의 모듈화
• 표준화된 GNN 평가: 데이터셋 분리도 설정할 수 있고, 어떤 평가지표를 쓸지, 성능 보고는 어떻게 할지 등을 결정할 수 있음.
• 재생산 가능하고 척도가 있는 실험 조정: config 파일로 적을 수 있음.
  • 새로운 GNN 모델을 공유하고 비교하기 쉽다
  • 알고리즘 발전 과정을 쉽게 트래킹할 수 있다
  • 커뮤니티 밖에 있는 연구자들도 발전된 GNN 디자인에 익숙해질 수 있다.

7.2 Experimental Setup

• 80/20 train/val 데이터셋 분리
  • 그래프 분류의 경우, inductive한 분리(학습에서는 사용 안된 데이터가 test에 사용됨)
  • 노드 분류의 경우, inductive 또는 transductive할 수 있음(훈련 그래프에서 보지 못한 노드들이 test에 사용됨)
• 검증 데이터셋의 마지막 epoch 성능이 보고됨
• 다중 분류에는 accuracy, 이중 분류에는 ROC AUC 점수가 사용됨

7.3 Results on GNN Design Space Evaluation

Ranking 분석 평가

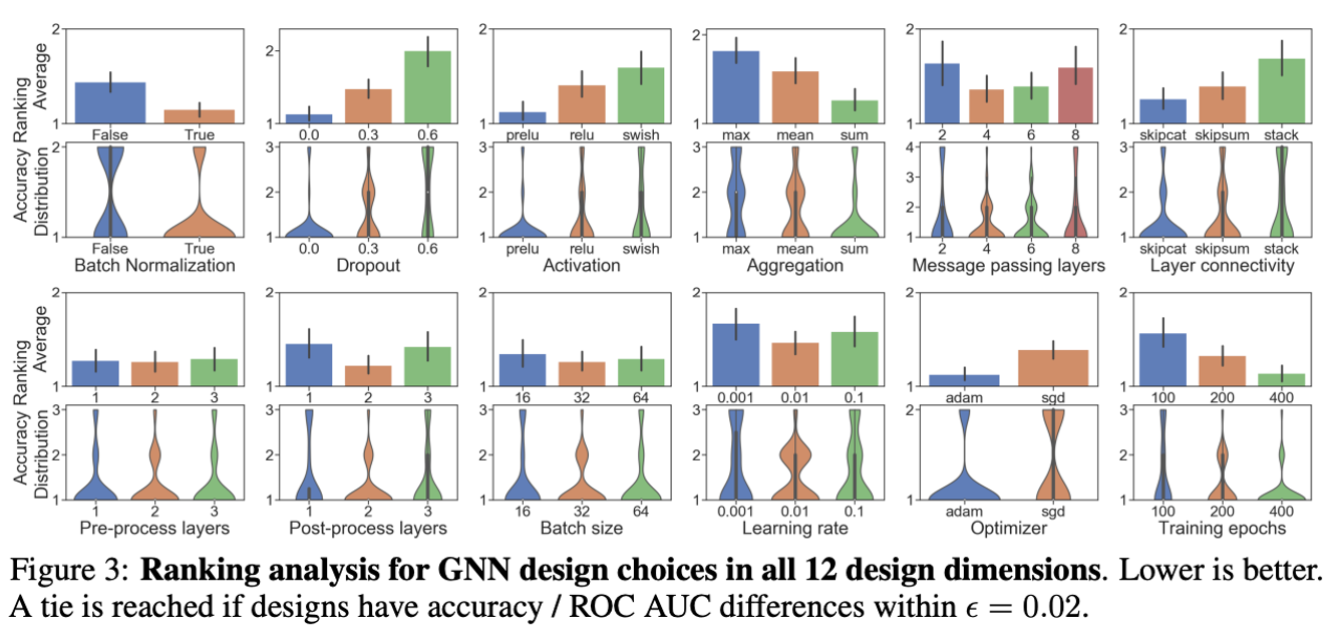
모든 96개(32개 task * 3번)의 세팅에 대해 12개의 디자인 차원의 각 요소끼리 순위를 매긴다.

• bar plot: 평균 순위값 (낮을수록 좋음)
• violin plot: 모든 96개 세팅들에 대한 디자인 차원 요소들의 부드러운 순위 분포. tie 상황에서 모두가 1등인 경우가 존재하기 때문에 violin plot은 1등이 안된 디자인 차원 요소가 무엇인지 파악하기에 좋다.

Findings

Intra-layer design 발견점

1. Batch Normalization을 추가하는 것이 좋다. 신경망 학습에 BN이 도움을 준다는 이전 연구도 있는 걸 보면 일맥상통한다.
2. Dropout은 안하는 것이 좋다. 이미 GNN은 neighborhood aggregation을 포함하고 있기 때문에 노이즈와 이상치에 대해 robust하다.
3. PReLU가 활성화 함수로 성능이 좋다. (기존에는 잘 안쓰던 함수였는데 매우 새로운 발견)
4. SUM aggregation이 이론적으로 가장 expressive한데 실험을 통해서도 결과가 동일하게 나왔다. (경험적으로 증명함)

Inter-layer design 발견점

1. Message passing layer의 개수에 대해서는 명확한 답이 나오지 않았다. 매우 다른 task에서 제일 잘 작동하는 건 2 또는 8개.
2. Skip connection을 쓰는 게 좋은데 Skip-sum보다는 Skip-cat이 더 좋은 결과를 보여준다.
3. (1)과 비슷하게 pre- 또는 post-processing layer의 개수도 task에 따라서 결정해야 한다.

Learning configurations 발견점

1. batch_size = 32 (3위에 들 가능성이 적어서)
2. Learning Rate = 0.01 (3위에 들 가능성이 적어서)
3. 옵티마이저 = Adam.(naive SGD보다 좋음). 튜닝된 SGD가 더 좋은 성과를 보여줌.
4. 더 많은 epoch 수가 더 나은 성능을 보여줌.

논문에서 제시한 평가 프레임워크는 GNN design dimension를 철저하게 확인할 수 있는 도구이다. 10M개의 모델-task 결합들에서 controlled random search를 진행함으로써 고정된 디자인에서 몇 개의 그래프 예측 문제들에 대해 평가하는 것보다 더 설득력 있는 가이드라인을 제공한다.

또한 다중 가설 검증 문제도 해결할 수 있다. ⇒ 12개 중 7개 design dimension이 GNN 성능에 큰 영향력이 있음을 밝혀냄 (one-way ANOVA with Bonferroni correction)

7.4 Results on the Efficacy of GNN Task Space

압축된 GNN design space

7.3에서 찾은 가이드라인에 기반해서 design dimension을 고정시켜 압축된 GNN design space를 만든다. ⇒ full-grid search를 가능하게 함.

1. 실제로 task space가 GNN task끼리 최상의 GNN design 이동이 가능한지 확인할 수 있음.
2. 큰 스케일의 데이터셋에 적용해봄으로써 경험적인 혜택이 있는지 검증할 수 있음.

Task들 사이에 선호되는 그래프 디자인들은 매우 다르다.

어느 데이터셋이냐에 따라 선호되는 디자인 차원의 요소들이 다름.

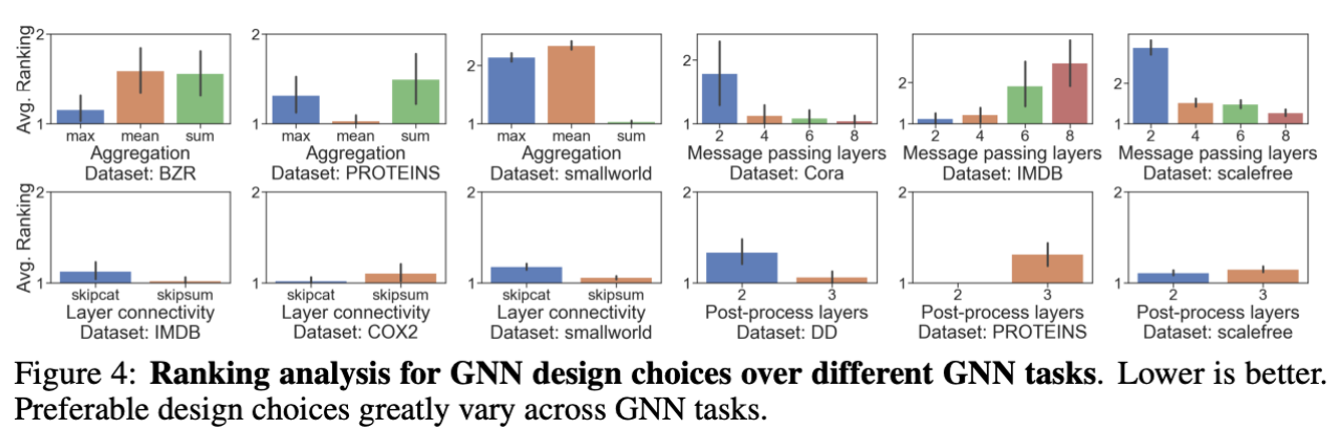
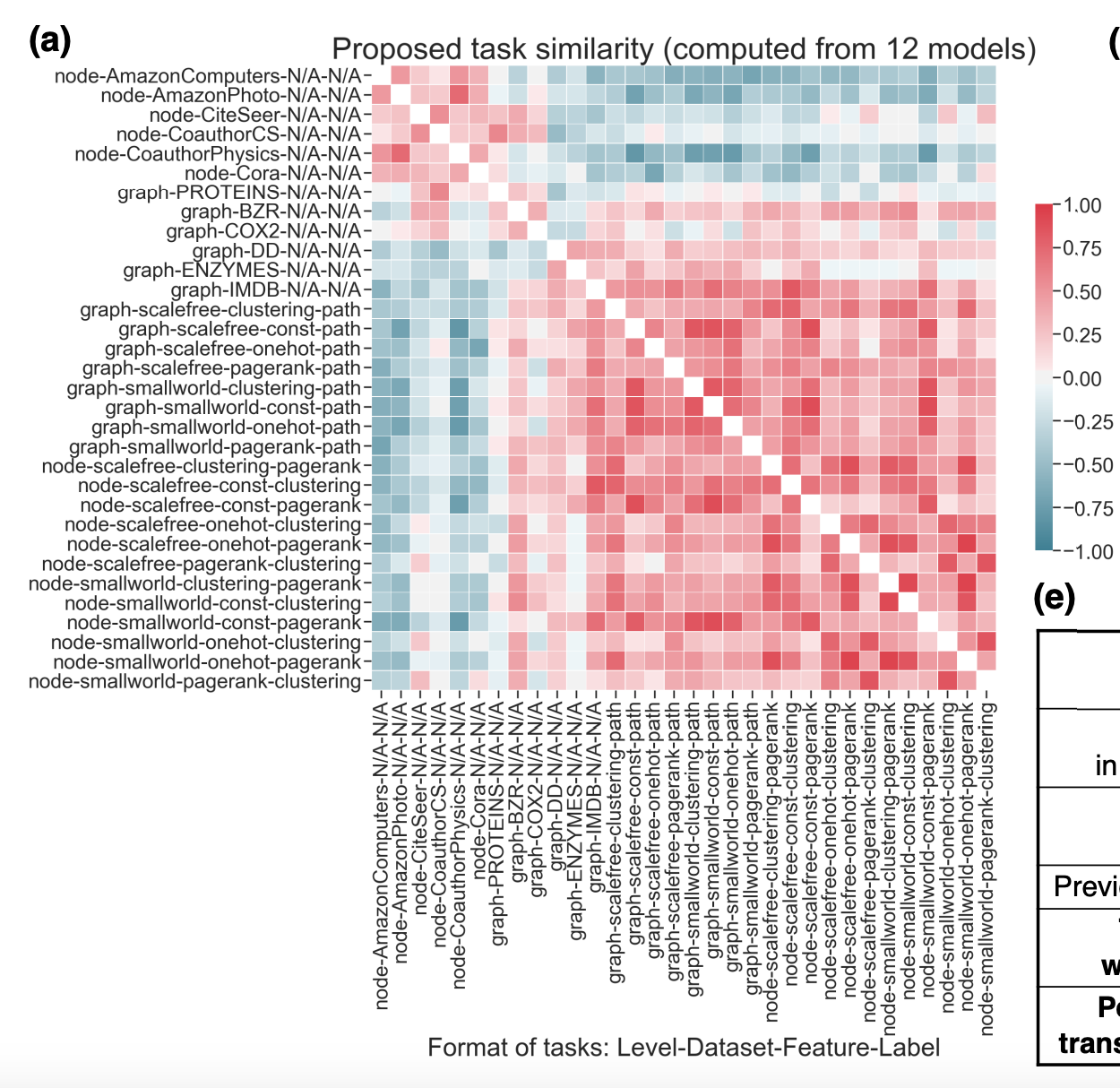
Task 유사도 평가지표를 통해 task space를 구축한다.

task들이 크게 두 그룹으로 군집될 수 있다.

1. real-world 그래프 노드 분류 문제
2. synthetic 그래프 노드 분류 문제와 모든 그래프 분류 문제

1번 문제는 풍부한 노드 특성들을 가진 노드 레벨의 task이라서 feature 정보를 전달하는 것이 선호되고, 이와 반대로 2번 문제는 구조적 정보를 전달하는 것이 효과적이다.

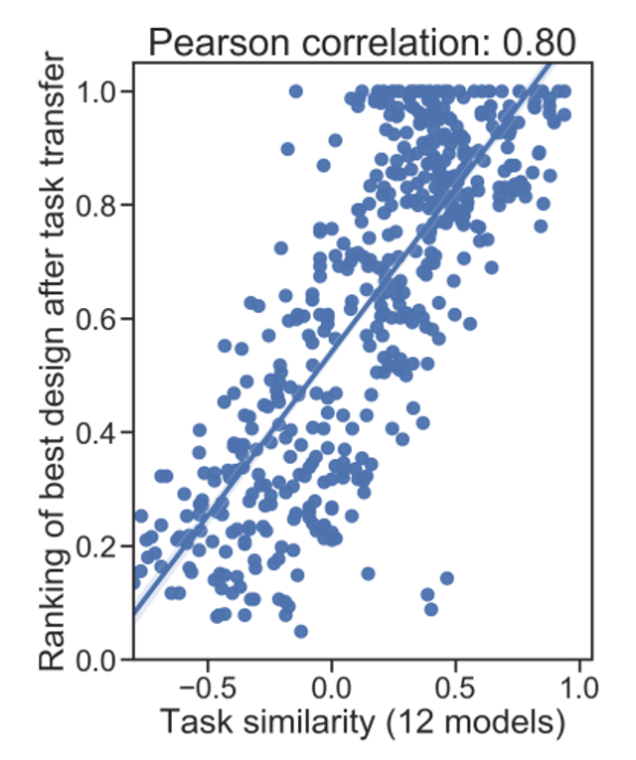
최적의 그래프 디자인은 높은 유사도를 가진 task로 이동할 수 있다.

최적의 모델을 하나의 task에서 다른 task로 옮기고 새로운 task에 대해 모델의 성능 순위를 측정할 수 있다. 실제로 두 task의 유사도와 다른 task로 이동한 후의 성능 순위 사이의 피어슨 상관계수가 0.8로 높은 값이 나옴.

즉, 논문에서 제시한 task 유사도 평가지표는 GNN 디자인이 새로운 task에 얼마나 잘 이동했는지를 보여준다.

표준 디자인과 최적 디자인 간의 비교

표준 디자인 → message passing layers 값이 {2,4,6,8} 안에 있고, 나머지 파라미터는 Table 1에서 찾은 최적의 값들로 설정한 표준 GCN.

최적 디자인 → 논문에서 제시한 design space에서 만든 모델

둘을 비교해본 결과, 32개 task 중에서 24개 task가 최적 디자인일 때 더 좋은 성능을 보였다.

강조: SOTA 성능을 추구하는 것이 목적이 아닌, GNN 그래프 디자인을 위한 시스템적인 접근을 보여주기 위함.

7.5 Case Study: ‘ogbg-molhiv’ 데이터셋 적용

design space로부터 96개 디자인을 추출 + task space로부터 task 유사도 평가지표 제작. (높은 유사도끼리는 디자인을 이동시킬 수 있도록)

[연구 문제]

1. 압축된 디자인 공간에 있는 최적 디자인이 SOTA 성능을 달성할 수 있는가?
2. grid search 없이 task 유사도만으로 이동할 그래프 디자인을 찾을 수 있는가?

1️⃣ 기존 모델보다 더 좋은 성능을 보여줌 (ROC AUC 0.792 vs 0.771)

2️⃣ 높은 유사도를 가진 task의 best design을 사용해도 기존 SOTA보다 좋은 성능을 보임 (0.785 vs 0.771)

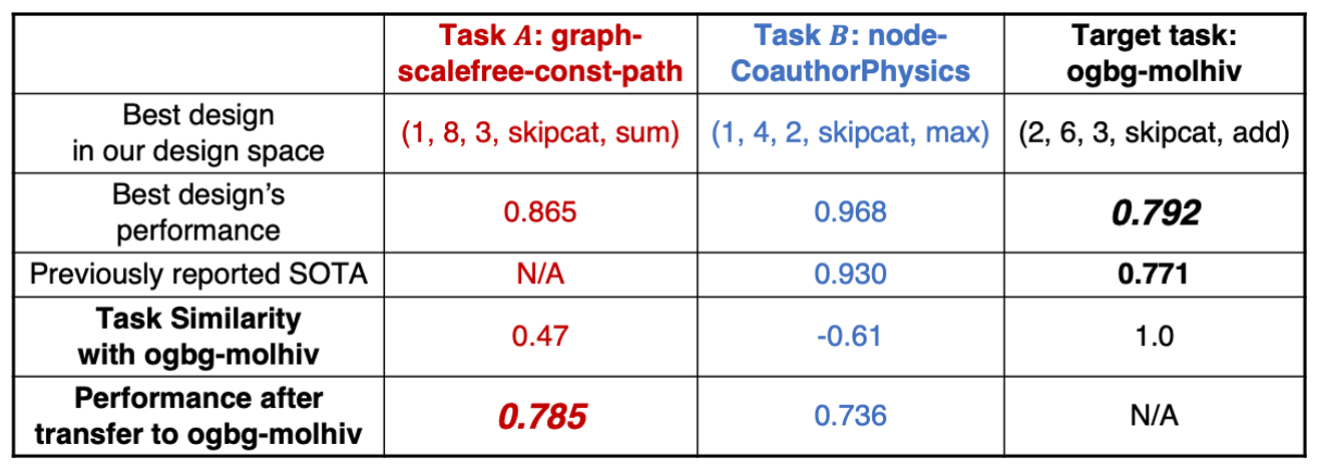
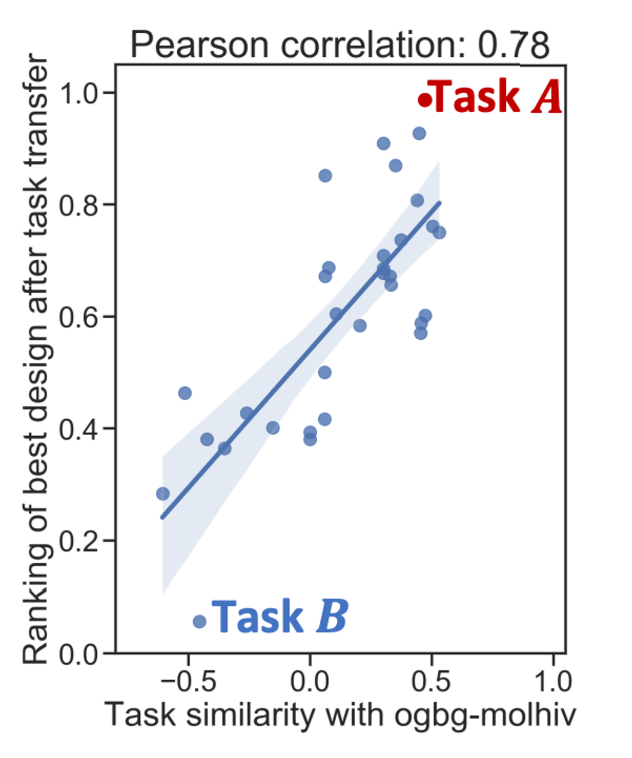
‘ogbg-molhiv’와의 유사도가 각각 0.47, -0.61을 가지고 있는 task A와 B를 선택 (비교를 위함)

• Task B: 본인의 best design 성능은 기존 SOTA보다 더 좋은 점수를 가졌지만 (0.968 vs 0.930) ‘ogbg-molhiv’에 적용했을 때는 0.736으로 더 낮은 성능을 가짐.
• Task A: 높은 task 유사도를 가지고 있기 때문에 A의 best design을 바로 적용해도 ‘ogbg-molhiv’의 기존 SOTA 성능보다 더 좋은 성능을 보일 수 있음.

8. Conclusion

GNN 디자인 공간과 양적 task 유사도 메트릭이 포함된 GNN task 공간을 design space 평가 방법과 함께 연구하는 것이 GNN 모델과 task들에 대한 새로운 이해를 이끌 수 있다.

알고리즘 개발 비용을 줄이고 경험적인 성능 또한 얻어낼 수 있다.

개별적인 GNN 디자인과 task 인스턴스를 공부하는 관점에서 공간의 개념으로 확장해 시스템적으로 연구하는 관점을 제시했다.

Broader Impact

GNN 연구: 모델 복잡성을 통제하는 원리를 충분히 적용함. GNN 인스턴스화가 아닌 GNN 디자인의 가이드라인 제시. 최적의 GNN 디자인이라 하더라도 다른 task에서는 성능이 낮아질 수 있다는 점 제시. 최종적으로 양적 유사도 평가지수로 측정되는 다양한 task에 대한 모델 평가 방법을 제시.

머신러닝 연구: 논문에서 제시한 controlled random search 방식이 일반적인 머신러닝 모델 디자인에 적용할 수 있다. 해당 알고리즘 개선점이 유용한지 보기 위해 모델-task 결합들을 랜덤으로 샘플링해서 성능이 좋아지는지 확인하는 것이 필요하다.

다른 연구 도메인: 도메인 전문가들이 적절히 포맷되어 있는 데이터셋만 제공한다면 추천된 GNN 디자인을 자동으로 적용시킬 수 있을 것이다. GNN 모델을 적용하는 것에 대한 장벽을 낮춰줌.