[CS224W] CH3. Node Embeddings

Graph Representation Learning

⇒ 자동으로 그래프의 feature 학습, 매뉴얼로 일일이 feature engineering할 필요를 완화시킴.

임베딩(embedding)의 필요성: 노드들을 임베딩 공간으로 매핑해주기 때문 (그래야 downstream task에 쉽게 적용할 수 있음)

• node 임베딩 간의 유사도는 네트워크 내에서의 유사도를 보여줌.
• 네트워크 정보를 인코딩하는 역할

Encoder and Decoder

Setup

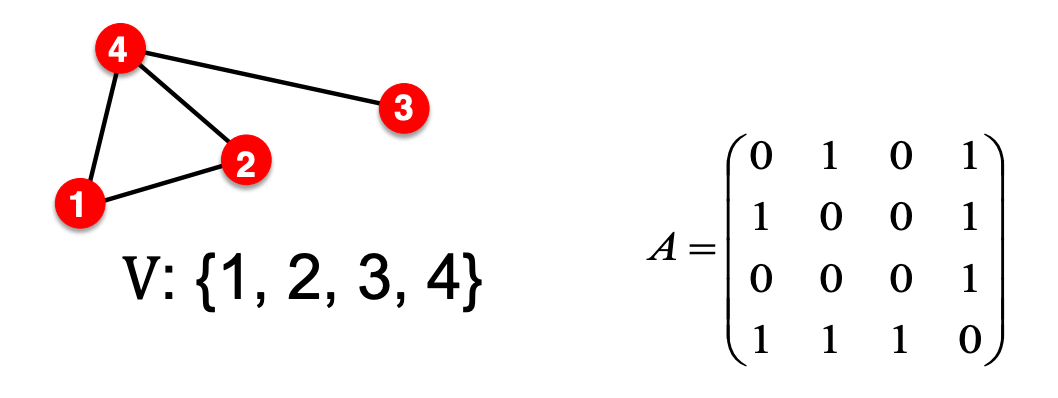
임베딩 공간에서의 유사도가 그래프에서의 유사도에 근접하도록 노드들을 인코딩하는 것이 목표.

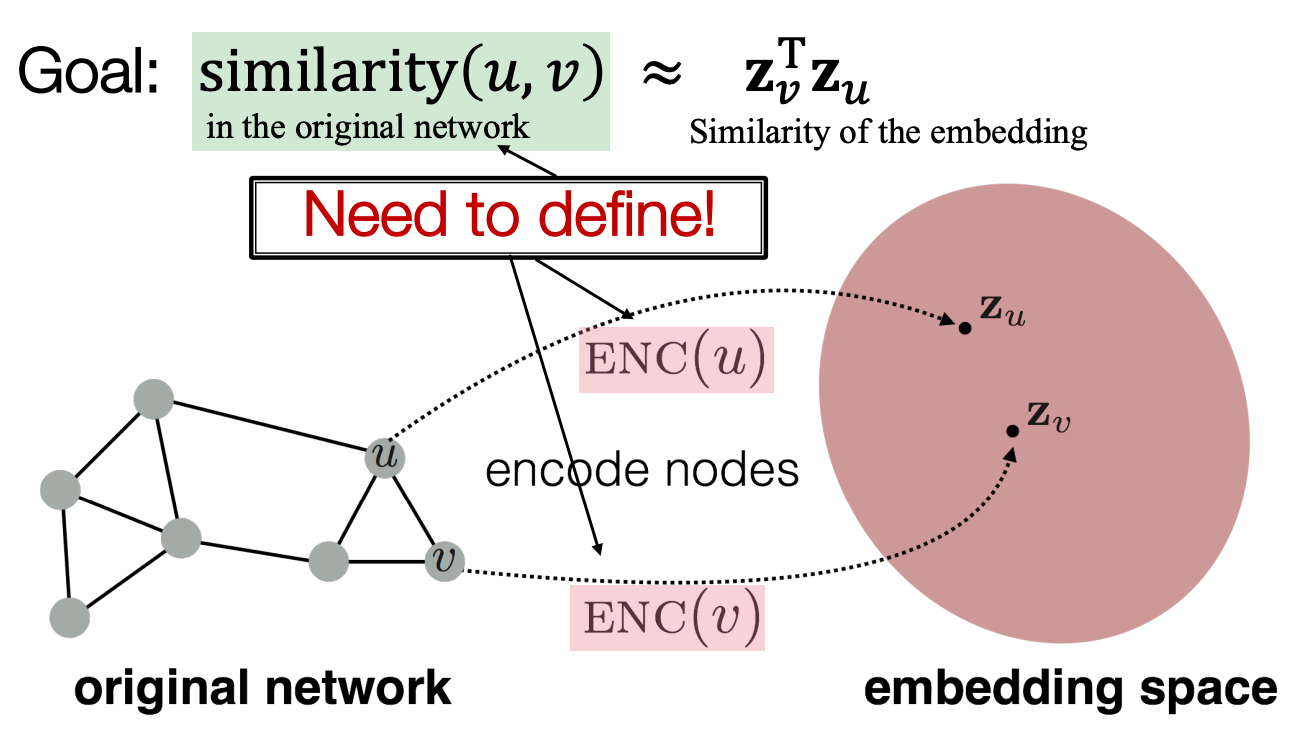
Learning Node Embeddings

[Encoder] 그래프의 노드를 임베딩으로 매핑 ⇒ 노드 유사도 함수(node similarity function)를 정의해야 함

[Decoder] 임베딩에서 유사도 점수로 매핑, representation learning의 목적 함수로 사용됨.

최종적으로 인코더의 파라미터를 최적화: $similarity(u,v) \approx {z_v}^Tz_u$

• 기존 네트워크의 유사도가 임베딩 공간에서의 유사도와 근사적으로 일치하도록 하는 인코더를 제작.

Two Key Components

1. Encoder: 각각의 노드를 Low-dimensional 벡터로 매핑
2. Similarity function: 어떻게 벡터 공간의 관계가 기존 네트워크의 관계와 비슷한지 알려주는 함수. Decoder는 노드 임베딩 벡터 간의 내적(dot product)으로 계산하는 경우가 많음.

Shallow Encoding

Encoder is just an embedding-lookup (인덱스로 값을 가져오는 것)

• Z는 우리가 최적화시켜야 할 행렬(각 열은 노드 임베딩 벡터) & v는 look up 벡터. v 노드를 나타내는 열만 1, 나머지는 0.
• 각 노드는 unique한 임베딩 벡터로 지정되어 있다 (= 각 노드의 임베딩을 직접 최적화시킨다)
• Z의 크기는 매우 큼(노드 마다 열 1개, 임베딩 사이즈(d=64~1,000)가 Z행렬의 column size)

Note on Node Embeddings

• 노드 임베딩 학습은 비지도/자기지도 학습 방법
  • 노드의 label이나 feature들을 사용해서 학습하지 않음.
  • 디코더로 얻어낸 네트워크 구조를 보존시키면서 노드의 좌표(임베딩)를 직접적으로 추정하는 것이 노드 임베딩의 목표.
• task independent: 특정 Task를 위해 훈련된 건 아니지만 어느 task든 사용될 수 있음.

Random Walk Approaches for Node Embeddings

Notation

• Vector $z_u$: 노드 u의 임베딩 벡터
• Probability $P(v | z_u)$: random walk로 노드 u에서 걷기 시작해 노드 v를 방문할 (예측된) 확률
• Non-linear functions for producing predicted probabilities
  • Softmax function: $S(z)[i] = \frac{e^{z[i]}}{\sum_{j=1}^Ke^{z[j]}}$ , K개의 실수값들을 K개의 확률값으로 변환(총합은 1). 지수함수를 활용하는 이유는 서로 간의 확률 차이를 키워서 확실히 구분하기 위함.
  • Sigmoid function: $\sigma(x) = \frac{1}{1+e^{-x}}$ , 실수 값을 0~1 사이의 값으로 대응시키는 함수.

Random Walk

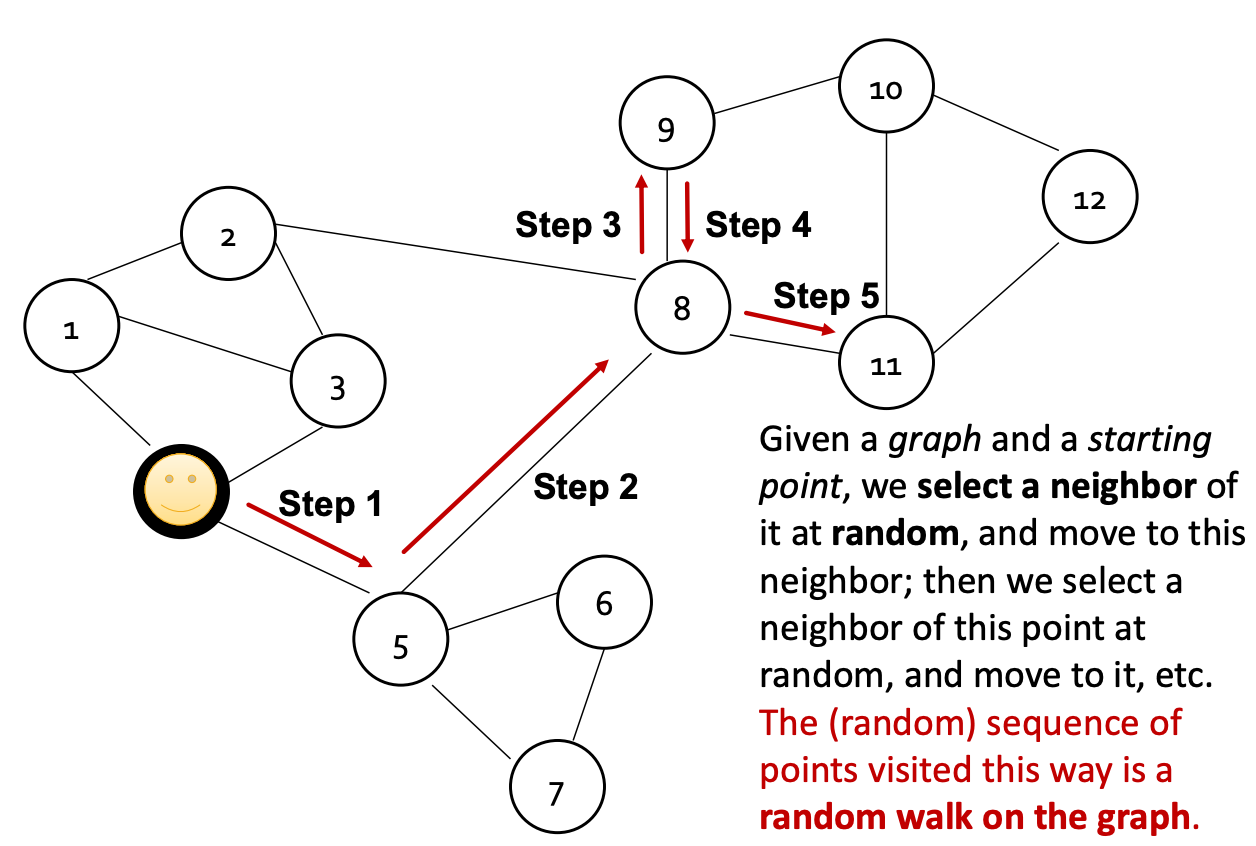
0. 가정: 그래프 G, 시작점 1개

1. 시작점에서 이웃 노드를 랜덤으로 선택한 후 그 이웃으로 이동 ⇒ 여러 차례 반복.

2. 그러한 방식으로 움직인 랜덤한 sequence of points = “a random walk on the graph”

   예) Step 1에서는 1,3,5 중에 선택, Step 2에서는 4,6,7,8 중에 선택.

${z_u}^Tz_v \approx$ 하나의 random walk에서 노드 u와 v가 동시에 나타날 확률

Random Walk Embeddings

1. 노드 u에서 시작한 random walk 전략 R을 사용했을 때 노드 v를 방문할 확률을 추정 ⇒ $P_R(v|u)$
   

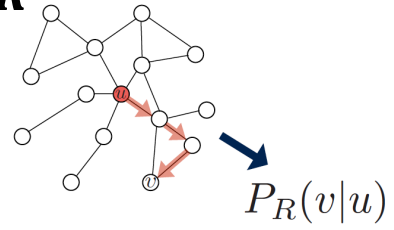
2. 그러한 random walk 통계량을 인코딩하는 임베딩 방법을 최적화
   

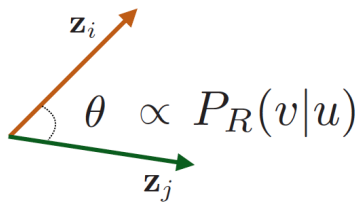
임베딩 공간에서의 유사도(=cos($\theta$), 여기서는 dot product)는 random walk 유사도를 인코딩해줌.

cos($\theta$))값이 커짐 = 내적 값이 커짐 = 두 벡터가 유사함.

Why Random Walks?

1. Expressivity: local + 고차원 이웃 정보를 모두 포함하는 node similarity를 확률적으로 유연하게 설명한다. 노드 u에서 시작한 Random walk가 노드 v를 높은 확률로 만난다면, u와 v는 유사하다. (high-order multi-hop information)
2. Efficiency: 학습할 때 모든 노드의 쌍에 대해 고려할 필요 없음. Random walk에서 동시에 나타난 쌍들만 고려하면 됨.

Unsupervised Feature Learning

• 직관: 유사성을 보존하는 d차원 임베딩 공간을 찾는 것.
• 아이디어: 네트워크에서 서로 근처에 있는 노드들이 비슷하도록 노드 임베딩을 학습.
• 노드 u가 주어졌을 때, 근처 노드들을 어떻게 정의하는가?
  • $N_R(u)$: random walk 전략 R에 의해 얻어진 u의 이웃 노드들

Random Walk Optimization

🔥 Goal: 그래프 $G = (V, E)$가 주어졌을 때 $f : u \rightarrow \mathbb{R}^d$ , 즉 $f(u) = z_u$ 함수를 학습시키는 것.

Log-likelihood 목적 함수: $\underset{f}{max}\sum_{u\in V}logP(N_R(u)|z_u)$

⇒ 노드 u가 주어졌을 때 random walk 이웃 $N_R(u)$의 노드를 예측할 수 있는 feature representations를 학습시키는 것

1. 각각의 노드 u에서 short fixed-length의 random walks를 시작.
2. 각 노드 u에서 $N_R(u)$를 얻는다. (노드 u에서 시작해 random walks로 만난 노드들의 multiset, 집합 안에 반복되는 요소가 있을 수 있음)
3. 노드 u가 주어졌을 때 그들의 이웃 노드를 예측할 수 있도록 임베딩을 최적화

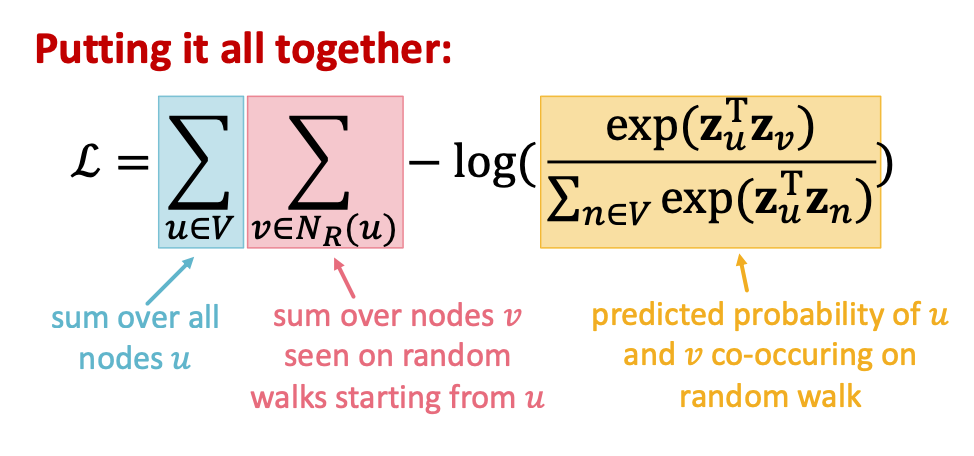
• 직관: random walk에서 동시에 나타나는 확률을 최대화하는 임베딩 벡터 $z_u$를 최적화하는 것. negative log likelihood인 L을 최소화시킨다.
• 소프트맥스 함수를 사용하여 $P(v|z_u)$ 파라미터화시킴
  

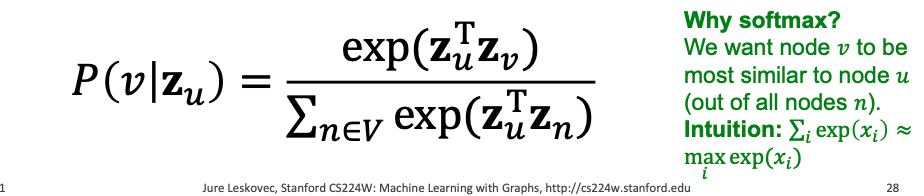
직접 이대로 수행하면 계산 복잡도가 너무 크다: V에 속한 모든 n과 u에 대해서 모두 더해줘야 하기 때문에 $O(|V|^2)$의 계산량이 나옴. -> 소프트맥스의 문제.

Negative Sampling

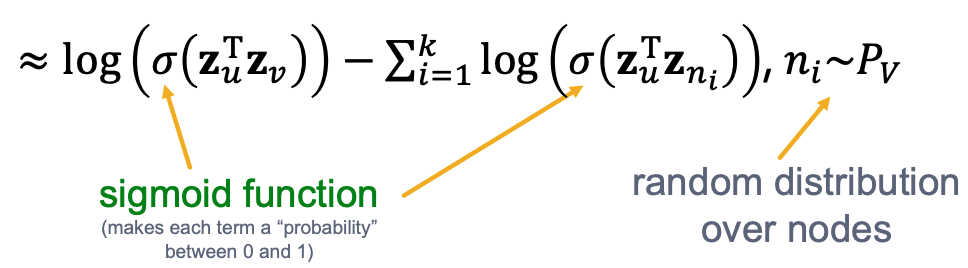i = negative samples. n_i = i개의 샘플을 랜덤으로 추출

naive한 방법은 모든 노드에 대해서 softmax 계산을 했다면, negative sampling은 노드의 부분집합만 가지고 계산해서 계산량을 줄인다.

** sigmoid 함수(logistic regression)를 사용해서 $P_v$ 랜덤분포에서 $n_i$ 노드들로부터 타겟 노드 v를 특정시킴.

• k개의 negative nodes $n_i$를 node degree에 따른 확률만큼 나오도록 샘플링
• negative sample 개수 k가 갖는 의미
  • k가 높을수록 robust한 추정이 나타난다. (극단값들에 민감하지 않다)
  • k가 높을수록 negative events에 높은 bias에 상응한다.
  • 일반적으로 k = 5~20

Stochastic Gradient Descent(SGD)

목적함수 L을 어떻게 최적화(최소화)시킬까?

Stochastic Gradient Descent: 모든 예시들에 대해 한꺼번에 gradient를 구하지 않고, 훈련 예시 각각에 대해서 gradient를 계산한다.

1. 모든 노드 u에서 랜덤한 값을 잡아 $z_u$를 초기화한다.
2. 수렴할 때까지 반복 : $L^{(u)}= \sum_{v \in N_R(u)}-\log(P(v|z_u))$
   • 노드 u를 샘플링하고 모든 v(이웃 노드)에 대해 gradient를 계산한다. $\frac{\partial L^{(u)}}{\partial z_v}$
   • 모든 v에 대해서 $z_v$를 업데이트한다. : $z_v \leftarrow z_v-\eta\frac{\partial L^{(u)}}{\partial z_v}$

How should we randomly walk? 전략 R을 어떻게 짜냐?

지금까지는 random walk를 사용해서 노드 임베딩 목적 함수를 최적화하는 방법에 대해 배웠다면, 이제는 random walk를 어떻게 해야하는가?에 대한 접근을 배워본다.

• simplest idea: Just run fixed-length, unbiased random walks starting from each node (진짜 랜덤으로) ⇒ 너무 경직된 유사도 개념
• 어떻게 일반화할 것인가? : use richer random walk

Node2Vec

Goal: 다양한 task에 적용 가능하도록 graph에서 node의 neighborhood 간의 유사성을 feature space(latent space, 관측 데이터를 잘 설명할 수 있는 잠재 공간) 상에서도 유지하는 것. ⇒ maximum likelihood optimization problem으로 해결

Key observation: 노드 u에 대한 이웃 네트워크 $N_R(u)$를 유연하게 정의하는 것이 rich한 노드 임베딩을 가져올 수 있음.

node2vec: Biased Walks

Idea: 네트워크의 local과 global views 사이의 trade off를 가능하게 하는 flexible, biased random walks를 사용한다.

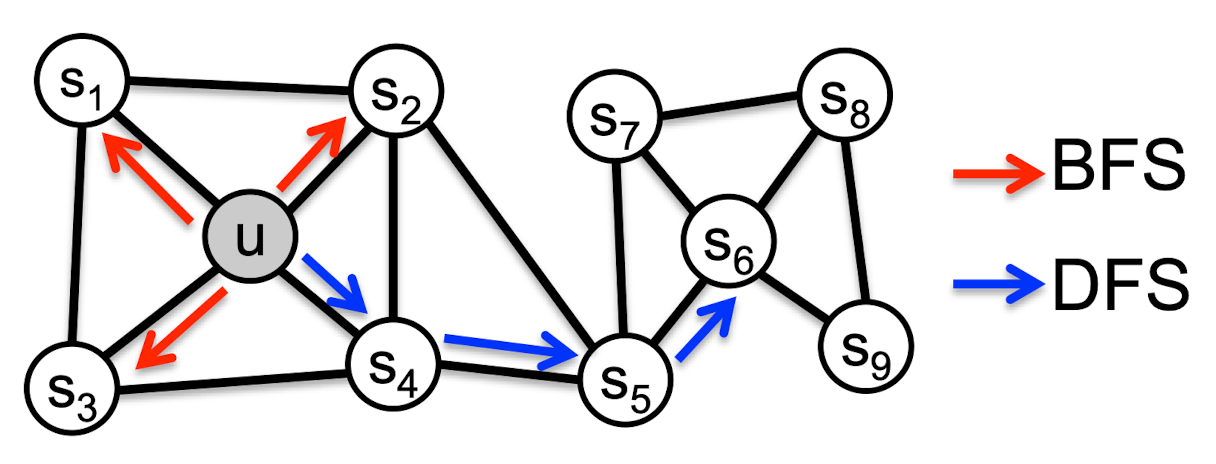
Walk of length 3 ($N_R(u)$ of size 3)

$N_{BFS}(u) = \{s_1, s_2, s_3\}$ Local microscopic view (Breadth First Search)

$N_{BFS}(u) = \{s_4, s_5, s_6\}$ Global macroscopic view (Depth First Search)

Interpolating BFS and DFS

Random walk has 2 hyperparameters:

• Return parameter p: 이전 노드로 돌아가는 것
• In-out parameter q: BFS와 DFS의 비율 조절(moving inwards vs. outwards)

Biased 2nd-order random walks

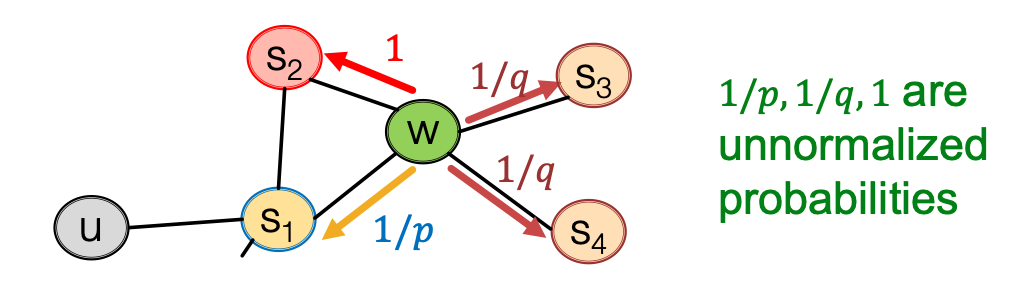
random walk가 (s1, w) 엣지를 타고 지금은 w에 있는 상태.

w의 이웃들은

• s1: 기존 노드로 돌아간다. 1/p 확률로 돌아가게 됨.
• s2: s1과 같은 거리에 있는 노드.
  • 확률값이 왜 1인가?: 우리가 갈 수 있는 방향은 3가지. 이미 2가지는 Parameter로 편향 조정이 가능하기 때문에 추가 파라미터 설정을 안하고 1로 둔다.
• s3: s1에서 멀어지는 노드. 1/q 확률로 멀어지게 됨.

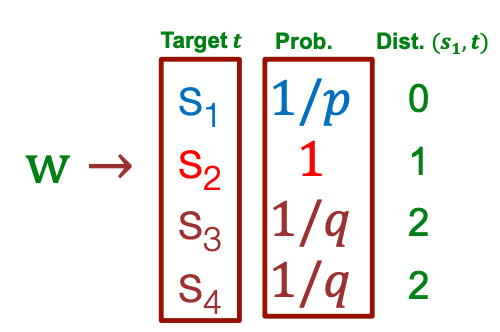
• BFS-like walk: 작은 p 값
• DFS-like walk: 작은 q 값

이렇게 biased된 확률을 가지고 이웃 노드들을 구하게 됨.

node2vec 알고리즘

1. random walk 확률을 구한다.
2. 각 노드 u에서 시작하는 $l$ 길이의 random walk를 r번 진행한다.
3. SGD를 사용해 node2vec 목적함수를 최적화한다.

• linear time complexity: 계산 복잡성이 낮음.
• 모든 3개의 과정이 병렬적으로 수행 가능하다
• 한계: 각각의 임베딩을 매 step마다 학습시켜야 함.

💡 어떤 방법이든 모든 과제에서 최고 성능을 보이는 방식은 없음. 일반적으로 random walk 접근이 더 효과적이지만 내가 하는 과제에 맞는 node similarity 개념을 사용해야 한다.

Embedding Entire Graphs

부분 그래프나 전체 그래프 G를 임베딩하고 싶음: $z_G$

Tasks: 독성인지 독성이 아닌 분자인지 분류, 변칙적인 그래프 알아내기 등

Approach 1

• 일반적인 graph embedding 테크닉을 (부분)그래프 G에 넣는다. (node2vec, deepwalk 등)
• 그 (부분)그래프에 있는 노드 임베딩의 총합 또는 평균을 구한다.
  $z_G = \sum_{v \in G} z_v$

Approach 2

“virtual node”: (부분)그래프를 표현하는 가상의 노드를 만들어서 graph embedding 테크닉을 사용한다.

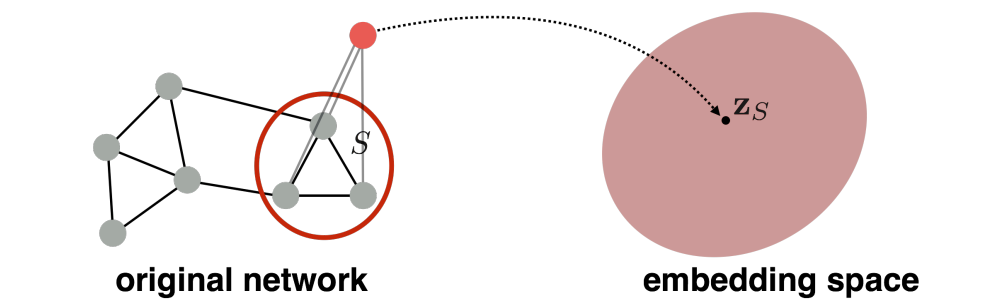
Approach 3: Anonymous Walk Embedding

• 정해진 길이의 random walk에 대해 각 노드의 인덱스를 지워 노드를 익명으로 만든다. 단, 중복으로 등장한 노드에 대해서는 처음 등장 시 사용했던 인덱스를 부여하게 된다.
• 방문 경로에 대한 기록을 남기는 셈.

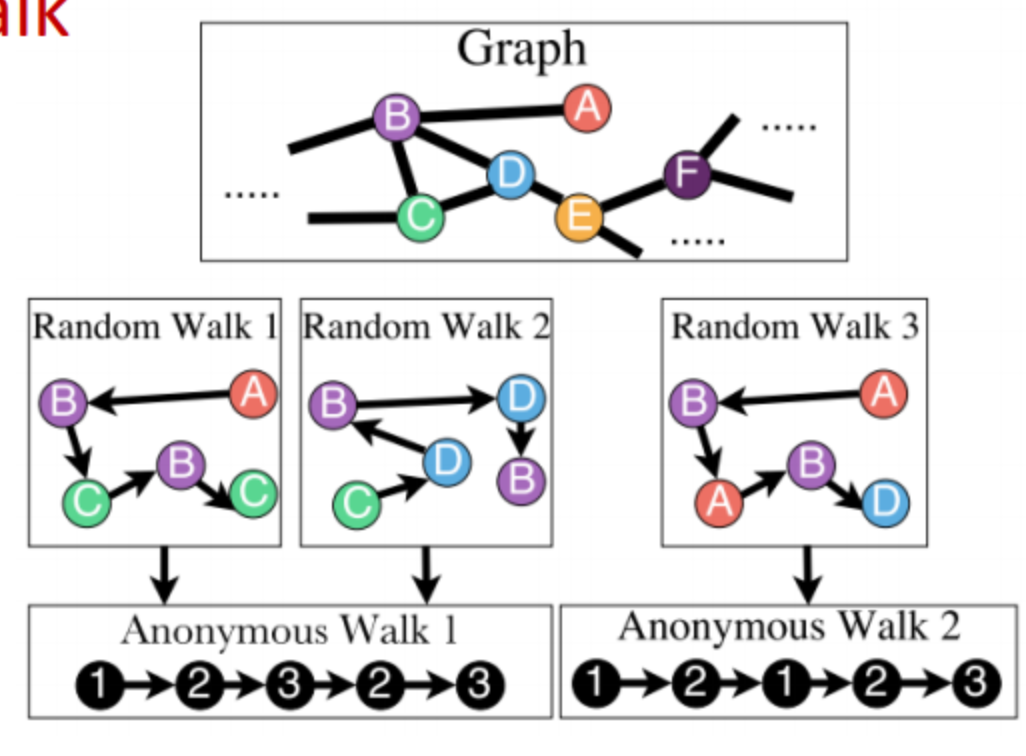
• 그러나 anonymous walks는 기하급수적으로 늘어난다.

[사용 방법]

• Set $l$ = 3 (#steps of anonymous walks)
• $l$ = 3일 때는 anonymous walk의 종류 개수는 5개이므로 5차원 벡터로 그래프를 표현할 수 있음.
  • 111, 112, 121, 122, 123
• $z_G[i]$ = 그래프 G에서 anonymous walk $w_i$의 확률

[Sampling anonymous walks]

m개의 독립적인 random walk를 만든다. ⇒ 이를 확률분포로 표현한다.

몇 개의 독립적인 random walk가 필요한가?

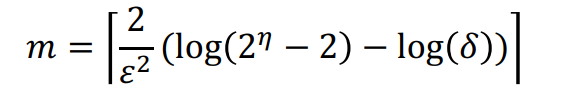
ϵ : 오차 하한, δ : 오차 상한, η : 길이가 l일 때의 총 anonyomous walk 수

통계 가설 검증할 때 특정 오차 범위 안에 들어가려면 해당 개수 m개의 random walk를 거쳐야 한다. (수리적인 증명을 거친 식)

New Idea: Learn Walk Embedding

단순히 각 walk의 빈도수를 임베딩 벡터로 사용하기보다는 walk 자체를 임베딩하여 사용하는 방법이 있음. (η은 샘플링된 anonymous walk 개수)

Idea: window size를 Δ라고 할 때, 동일한 노드에서 출발한 $w_{t-Δ}, ... , w_{t+Δ}$를 이용해 $w_t$를 예측하자.

• 예시: Δ=2일 때 w1, w2를 받고 w3을 예측함.

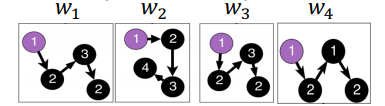
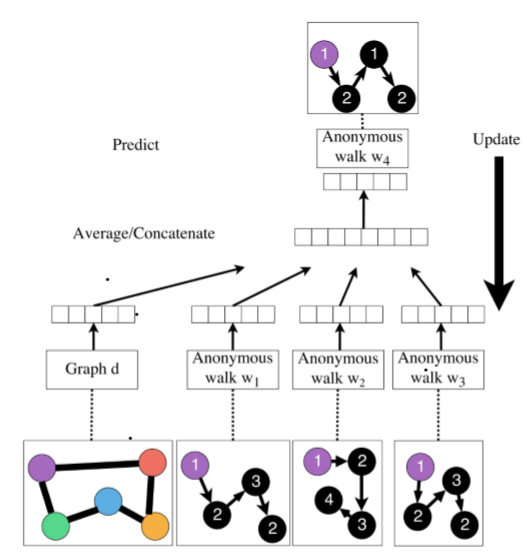
[목적 함수] $z_G$는 graph embedding.

[학습 방법]

1. 노드 u에서 각각 $l$ 길이의 random walk를 T번 진행한다.

$N_R(u) = \{{w_1}^u, {w_2}^u, ..., {w_T}^u\}$

2. window size Δ만큼 동안 동시에 나타난 walks를 예측하게끔 학습. 이때의 목적함수는 다음과 같다.

• 여기서 중요한 건 anonymous walk 임베딩과 함께 그래프 임베딩을 같이 학습시키는 것.
• $P(w_t|\{w_{t-Δ}, ... , w_1, z_G\}) = \frac{\exp (y(w_t))}{\sum_{i=1}^η\exp(y(w_i))}$ (softmax 함수로 파라미터 만들기, Negative sampling 사용)
• $y(w_t) = b + U \cdot(cat(\frac{1}{Δ}\sum^Δ_{i=1}z_i, z_G))$
• $b \in\mathbb{R}, U \in\mathbb{R}^D$는 학습 가능한 파라미터들. linear layer를 표현함.

3. 최적화 이후에 그래프 임베딩 $z_G$를 얻게 됨 (학습 가능한 파라미터)

⇒ 단어와 문단의 관계처럼 하나의 그래프의 동일한 노드에서 나온 random walk를 이용하여 해당 노드에서 나온 다른 Random walk를 예측할 수 있을 것.

4. $z_G$를 사용하여 예측 진행 (예: 그래프 분류)

• 옵션1: 내적 커널 ${z_{G_1}}^Tz_{G_2}$
• 옵션2: 그래프 G를 분류하기 위해 $z_G$를 입력으로 받는 신경망 사용

Preview: Hierarchical Embeddings

그래프에서 노드를 계층적으로 군집화할 수 있다. ⇒ 해당 군집에 따라 노드 임베딩을 합치거나 평균을 낼 수 있다.

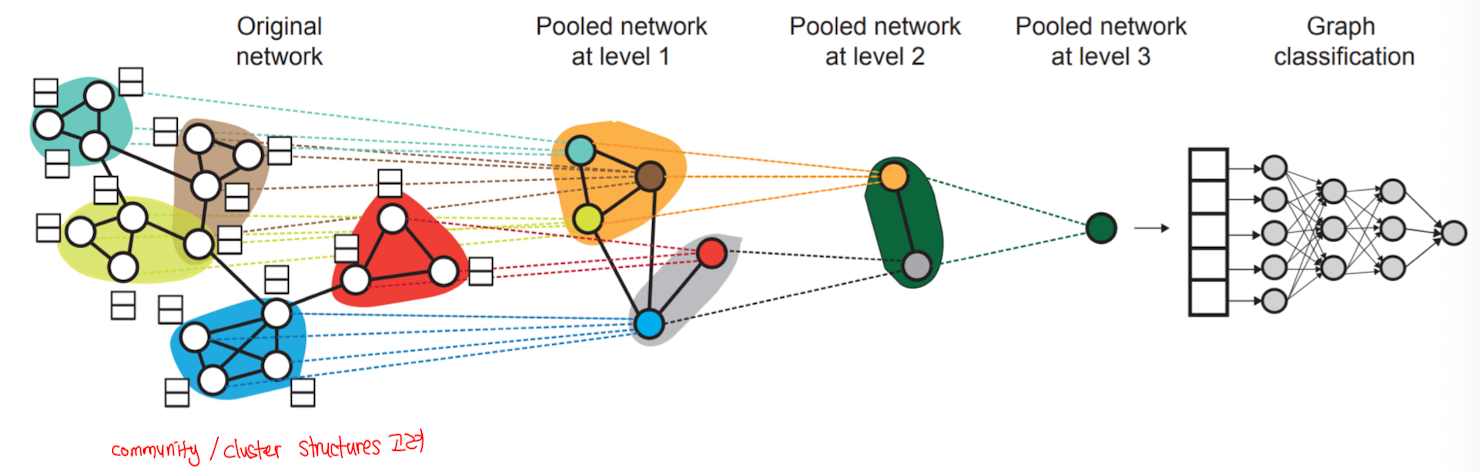
[임베딩 사용 방법]

• Clustering detection: 클러스터 포인트 $z_i$
• Node classification: $z_i$를 기반으로 노드 i의 label 예측
• Link prediction: $(z_i, z_j)$를 기반으로 엣지 (i,j)가 있는지 없는지 예측
  • 함수는 여러가지가 있을 수 있음. concatenate, hadamard, Sum/Avg, distance 등등
• Graph classification: 노드 임베딩 합치기 또는 anonymous random walks로 구한 그래프 임베딩 $z_G$로 label 예측