[CS224W] Ch6. Graph Neural Networks

0. Introduction

노드 임베딩: 그래프에서 비슷한 노드들끼리는 d차원 임베딩 공간에서 서로 가깝도록 매핑한다. 어떻게 매핑 함수 f를 학습시킬까?

목표: $similarity(u,v) \approx z_v^Tz_u$,
(1) 유사도 개념과 (2) 인코더 정의 필요.

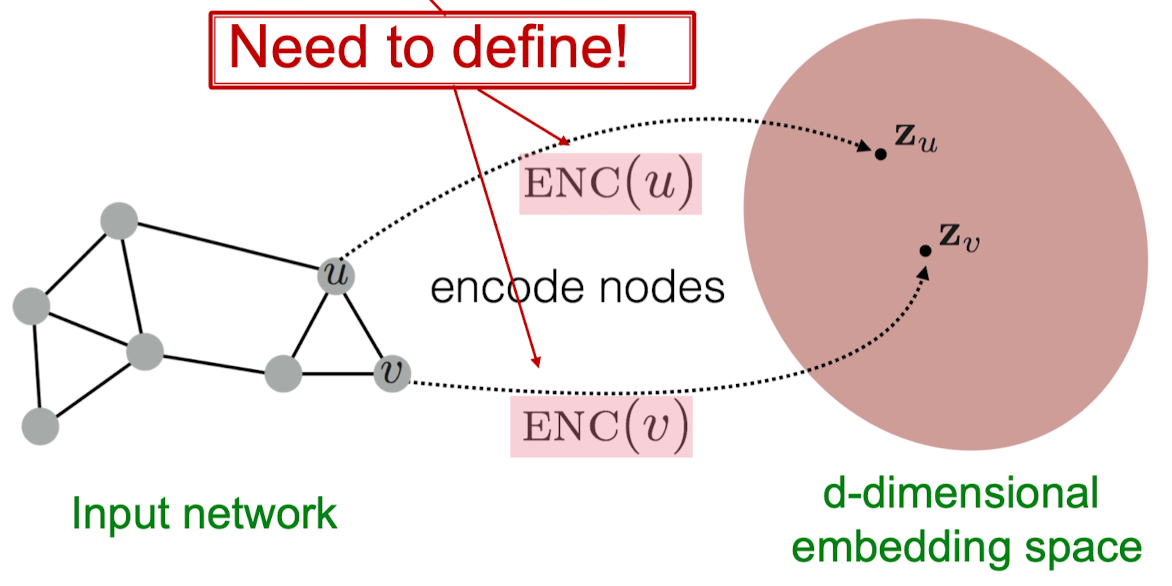
(1) 인코더(Encoder): 그래프의 각 노드를 low-dimensional 벡터와 매핑

• v = 입력 그래프의 노드

• $z_v$ = d차원 임베딩 벡터

(2) 유사도 함수(Similarity function, Decoder): 벡터 공간에서의 관계가 실제 네트워크의 관계와 매핑되는지를 구체화시키는 함수

• similarity(u,v) = 실제 네트워크에서 u와 v의 유사도

• $z_v^Tz_u$ = 임베딩 벡터끼리의 내적 값

“Shallow” Encoding

가장 단순한 인코딩 접근: embedding-lookup

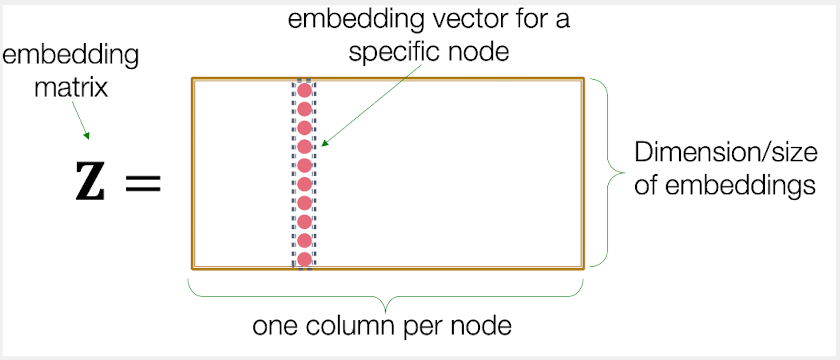
[한계점]

• O(|V|)개의 파라미터가 필요하다.(계산 복잡도↑)
  • O(_): '알고리즘 수행에 필요한 단계 수'
  • 노드 간에 공유하는 파라미터가 없음.
  • 매 노드마다 유일한(unique) 임베딩 벡터를 가지고 있음.
• inherently “transductive”(형질 전환)
  • 데이터 훈련 과정 동안 보이지 않은 노드에 대해서는 임베딩을 만들 수 없다.
  • transductive: can only make predictions over examples that we have actually seen during training phase.
  • ←→ inductive learning: 전통적인 머신러닝과 같이 test data를 철저히 분리한 상태에서 train data만을 이용해 학습과정을 수행. Inference는 train과 test의 distribution이 동일하다(iid)는 가정으로부터 실시됨.
• 노드 특성들을 사용할 수 없다
  • 많은 그래프들은 우리가 활용해야 할 많은 Feature들이 있다. (메타 정보)

Deep Graph Encoders

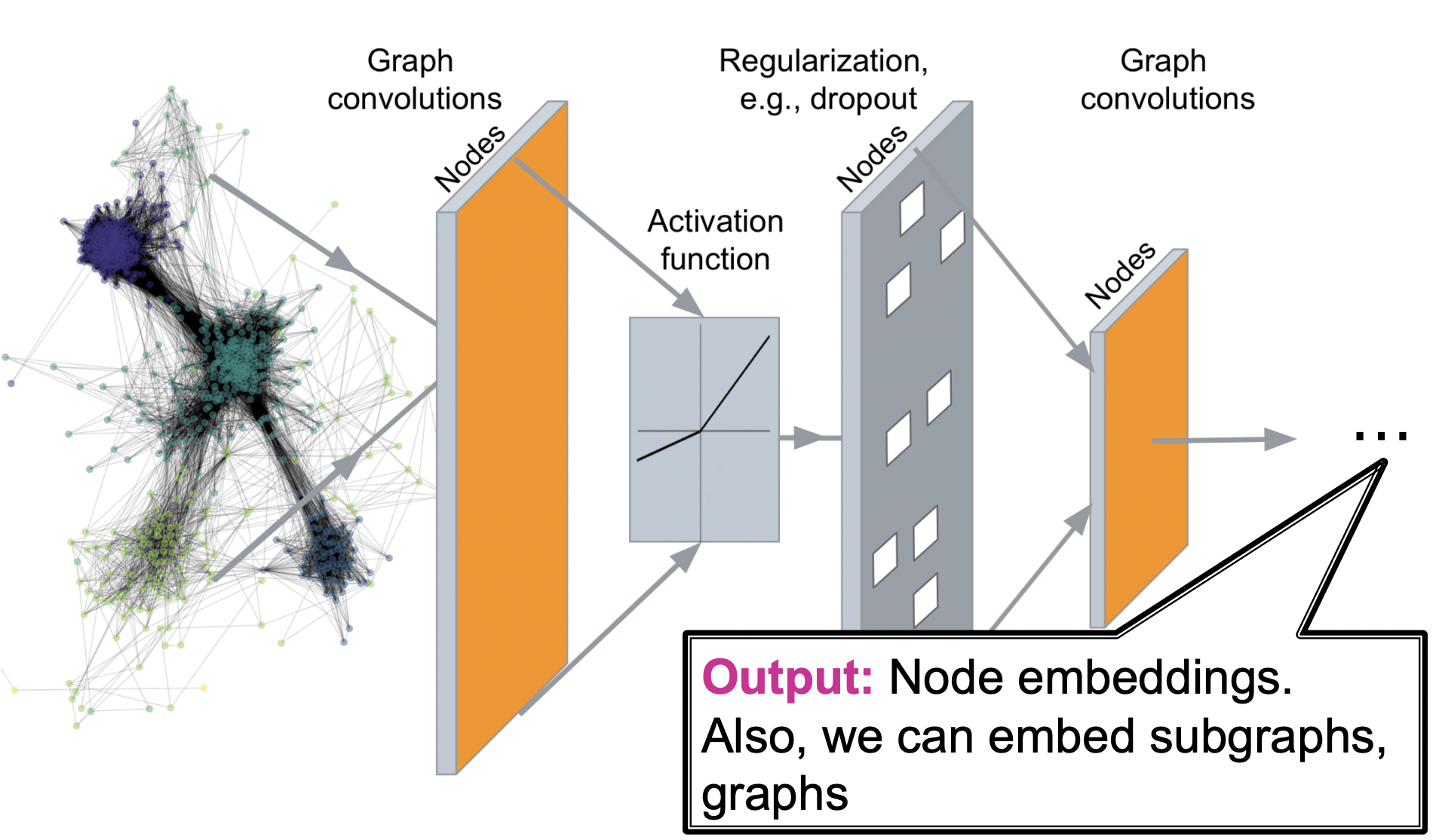
• GNN에서는 multiple layer로 구성된 인코더를 사용한다.
• 이를 통해 node classification, link prediction, community detection, network similarity와 같은 task 수행이 가능하다.
• GNN의 output은 노드의 임베딩일 수 있고, subgraph 또는 graph 자체의 임베딩일 수 있다.

현대 머신러닝 Toolbox

현대 딥러닝 toolbox는 단순한 시퀀스와 그리드를 위해 디자인되어 있다.

• 이미지 → 픽셀 기반 그리드, 텍스트/음성 → 시계열(시퀀스)

그러나 그래프는 훨씬 더 복잡하다!

• 임의적인 크기(arbitrary size)와 복잡한 위상적 구조(그리드와 같이 공간적 국소성이 없다. spatial locality)
• 고정된 포인트나 방향개념이 없다.
• 주로 유동적일 수 있고(dynamic) 다양한 feature들로 구성되어 있다.

1. Basics of deep learning

Machine Learning as Optimization

• 지도학습: 입력 x가 주어졌을 때, 레이블 y를 예측하는 것이 목표

  • 입력은 실수 벡터, 시퀀스(NLP), 행렬(이미지), 그래프(노드와 엣지 feature)가 될 수 있다.

• 우리는 이 task를 최적화 문제(optimization problem)로 만든다.

Θ: 우리가 최적화할 파라미터 집합

• 1개 또는 그 이상의 스칼라, 벡터, 행렬을 포함할 수 있다.
• Shallow Encoder에서는 Θ = {Z} (=embedding lookup)

L: 손실 함수(loss function)

• $\mathcal{L}(y,f(x)) = ||y-f(x)||_2$ (L2 loss, 회귀 문제에서 사용)
• 손실 함수 예시: cross entropy(CE)
  • label y = 범주형 벡터(원-핫 인코딩), $y = [0,0,1,0,0]$
  • f(x) = softmax(g(x)), $f(x) = [0.1, 0.3, 0.4, 0.1, 0.1]$ ** $f(x)_i = \frac{e^{g(x)_i}}{\sum^C_{j=1}e^{g(x)_j}}$
    
  • $CE(y, f(x)) = -\sum^C_{i=1}(y_i\log f(x)_i)$
    • $y_i, f(x)_i$ 각각은 실제 i번째 label 값과 예측값.
    • loss가 작을수록 one-hot 벡터 예측에 더 가까워진다.
  • 모든 훈련 데이터셋에 대한 총 손실: $\mathcal{L} = \sum_{(x,y) \in 𝒯}CE(y, f(x))$
    • 𝒯 = (x,y) 데이터 모든 쌍을 포함하는 훈련 셋

목적 함수를 최적화하는 방법

• Gradient 벡터: 가장 빠른 증가(최대 증가율)의 방향과 속도

• 주어진 벡터에 대한 다변량 함수의 방향도함수(directional derivative)는 해당 벡터가 함수에서 즉각적으로 변화하는 속도를 나타낸다.
• Gradient는 가장 큰 증가 방향을 보이는 방향도함수이다. 우리의 관심은 감소이므로 우리는 gradient의 반대 방향으로 walk down한다.

Gradient Descent

반복적인 알고리즘: gradient 방향의 반대 방향으로 가중치를 반복적으로 업데이트한다. (수렴할 때까지)

Training: Θ를 반복적으로 최적화한다. $Θ \leftarrow Θ - \eta\nabla_{Θ}\mathcal{L}$

• Iteration: Gradient descent의 1 step

$\eta$: 학습률(learning rate)

• gradient step의 크기를 조절할 수 있는 하이퍼파라미터
• 훈련하는 과정 동안 달라질 수 있다 (LR scheduling): 시작 단계에서는 큰 step을 밟지만 가면 갈수록 작은 step을 밟아야 함 (overstep하지 않기 위함)

이상적인 조건: 0 gradient

• 실제로는 validation set에서의 성능이 나아지지 않을 때 훈련을 멈춘다.

Minibatch SGD

gradient descent의 문제점: 모든 데이터 포인트에 대한 gradient를 전부 더한다. 즉 한번 한번 gradient descent step을 밟을 때마다 계산이 많아지고 느려진다.

⇒ Stochastic gradient descent(SGD)로 해결하기: 매 step마다 다른 minibatch B를 선택해서 input x로 사용한다.

• 필요한 기본 개념들
  • Batch size: 미니배치 안에 들어 있는 데이터 개수
  • Iteration: 미니배치에 대하여 SGD에서의 1 step
  • Epoch: 모든 데이터셋을 한 번 도는 것. (Iteration 개수는 (데이터셋) / (배치 사이즈))

SGD는 batch 배정을 uniformly random하게 진행하면 unbiased한 estimator이다.

• 그러나 수렴한다는 보장이 없음.
• 학습률 튜닝을 필요로 함
• SGD보다 더 좋은 optimizer: Adam, Adagrad, Adadelta, RMSprop …

Neural Network Function

목적함수: $\min_ΘL(y, f(x))$

• linear function $f(x) = W\cdot x,~~~Θ=\{W\}$

  • f가 스칼라 값을 내놓는다면 W은 학습 가능한 벡터

    $\nabla_{W}f = (\frac{\partial f}{\partial w_1}, \frac{\partial f}{\partial w_2},\frac{\partial f}{\partial w_3}~...)$

  • f가 벡터를 내놓는다면 W는 가중치 행렬(Jacobian matrix) ⇒ $\nabla_{W}f = W^T$

• 더 복잡한 함수 $f(x) = W_2(W_1 x),~~~Θ=\{W_1, W_2\}$
  • chain rule
    $\frac{dz}{dx} = \frac{dz}{dy}\cdot\frac{dy}{dx}$
  • 예시 적용: $\nabla_{x}f = \frac{\partial f}{\partial W_1x}\cdot \frac{\partial W_1x}{\partial x}$

Back-propagation(역전파): chain rule을 써서 즉각적인 step의 gradient를 뒤로 전파하여 최종적으로 Θ에 대한 L의 gradient를 얻는다.

• $f(x) = g(h(x)) = W_2(W_1 x)$
• $L = \sum_{(x,y)\in B}||(y-f(x))||_2$ ⇒ 미니배치 B의 L2 loss를 전부 더함
• 은닉층: 입력 x에 대한 중간 표현
  • $h(x) = W_1x, ~~~f(x) = W_2h(x)$
• Forward propagation(순전파): 입력에서부터 loss 계산 시작
• Back-propagation: $Θ=\{W_1, W_2\}$에 대한 gradient를 계산한다.

Non-linearity(비선형성)

: 결국 W2W1도 또다른 행렬. 아직 f(x)는 선형적이다.

• Rectified linear unit(ReLU)
  • $ReLU(x) = max(x, 0)$
• Sigmoid
  • $\sigma(x) = \frac{1}{1+e^{-x}}$

최종적으로 Multi-layer Perceptron(MLP)의 각 layer는 선형변환과 비선형성을 결합한다.

• $x^{(l+1)}=\sigma(W_1x^{(l)} + b^l)$

2. Deep learning for graphs

A Naive Approach

: 인접 행렬과 노드 특성들을 붙여서 deep 신경망에 feed한다.

문제점 발생!

• O(|V|) 파라미터 ⇒ 계산이 복잡함
• 다른 사이즈의 그래프에 적용할 수 없음
• 노드 넘버링이 달라지면 행렬도 달라짐. 예민함.

Idea: Convolutional Networks

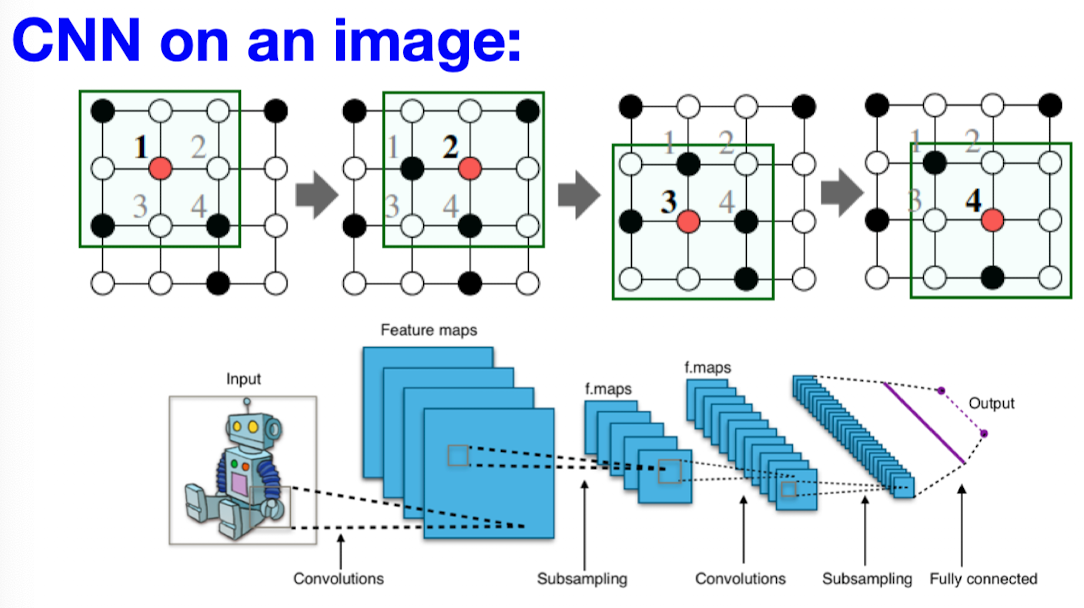
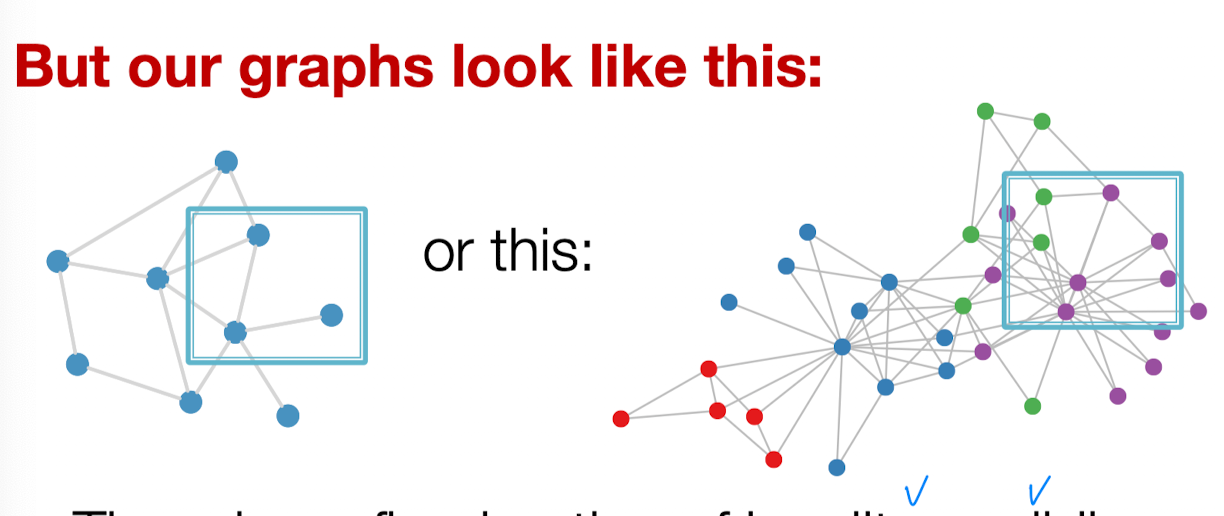
단순한 격자를 넘어서 노드 특성들을 적용할 수 있는 합성곱으로 일반화하는 것이 우리의 목표.

• 그러나 locality나 그래프에서의 윈도우 슬라이딩에 대한 고정된 개념이 없다.
• 그래프는 permutation invariant(순서 불변성 = 입력 벡터 요소의 순서와 상관없이 같은 출력을 생성한다). CNN의 Convolution 개념을 그대로 적용할 수 없다.

Idea: 이웃들로부터 정보를 받아서 결합한다.

• h_i라는 ‘메시지’를 이웃들로부터 받는다: $W_ih_i$
• 그리고 그걸 다 더함 $\sum_iW_ih_i$

Graph Convolutional Networks(GCN)

Idea: 노드의 이웃이 계산 그래프를 정의한다. (신경망 구조를 정의한다)

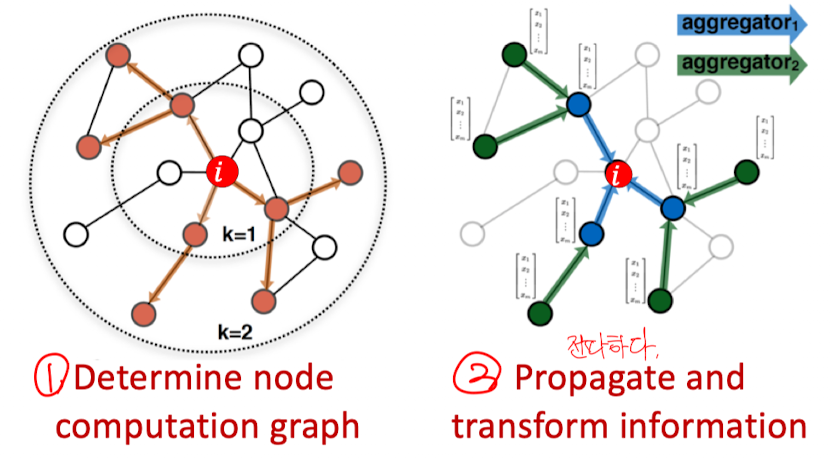
Idea: 이웃들을 모아라! (Aggregation)

Key Idea: local 네트워크 이웃들에 기반하여 노드 임베딩을 만든다. 노드들은 신경망을 이용해서 그들의 이웃들로부터 정보를 종합한다.

그래프 노드의 feature를 Latent vector로 두고 이웃 노드를 통해 정보를 취합한다.

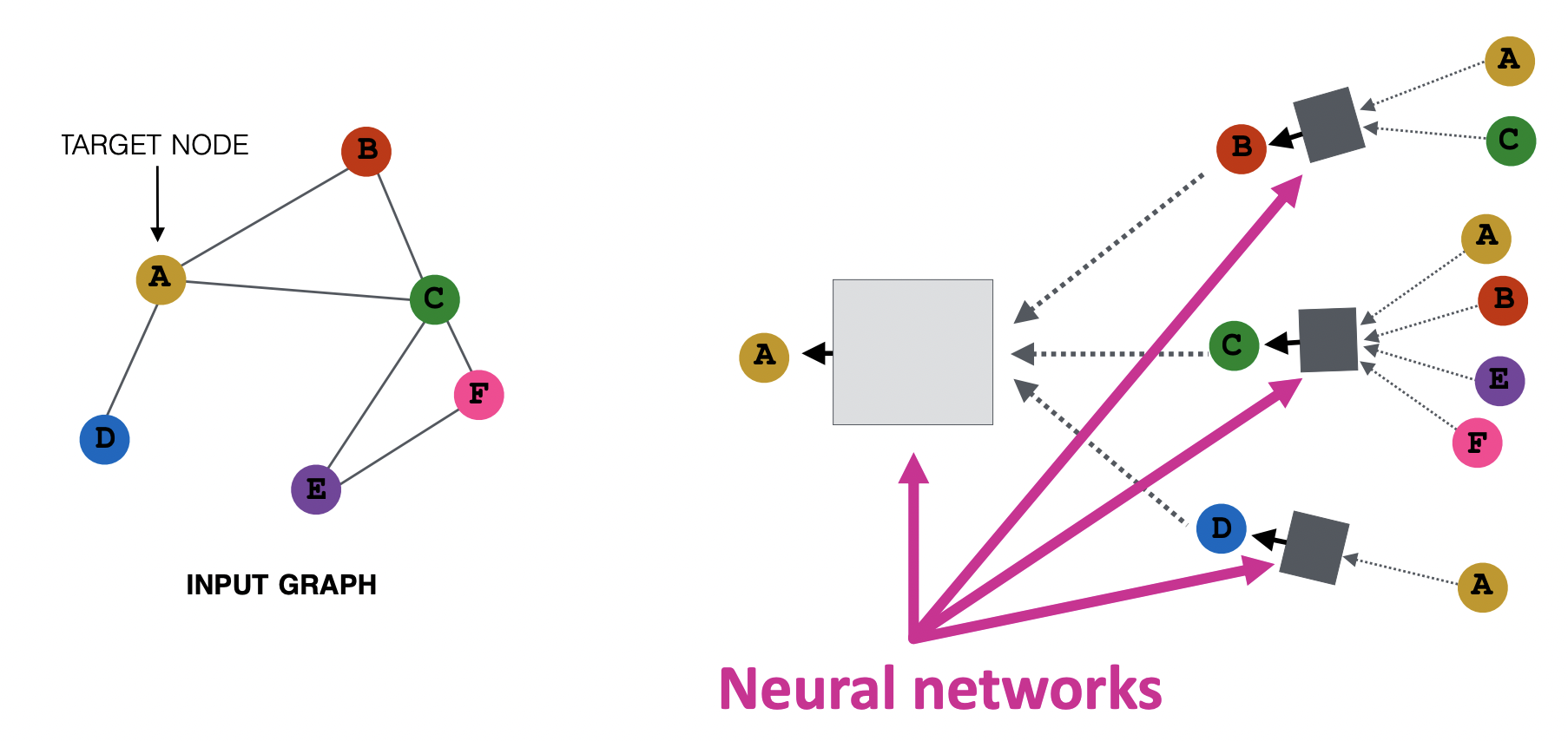
• 2개의 레이어를 거치도록 신경망을 구성하면 target node인 A는 그의 이웃인 B,C,D로부터 정보를 받고 각 이웃도 그들의 이웃들로부터 정보를 받는다.
• 가장 오른쪽에서부터 Layer 0. Layer 1에 있는 B는 A와 C, 그리고 자기 자신의 정보를 포함하고 있기 때문에 Layer 0에 있는 B와 다른 노드 임베딩을 지니고 있다.
  • 모델은 임의적인 깊이를 가질 수 있다 (arbitrary depth)
• u의 Layer-0 임베딩은 입력값 $x_u$
• Layer-K 임베딩은 K hop 떨어진 노드들로부터 정보를 얻는다.

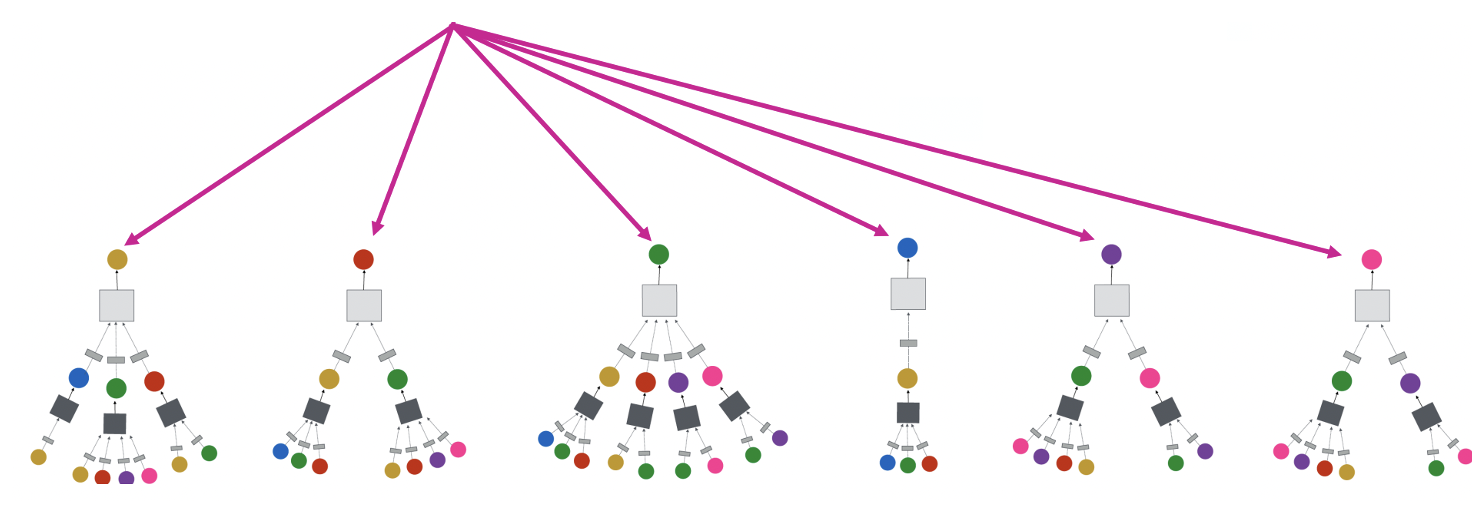
** 각 노드는 그의 이웃 노드들에 기반해서 계산 그래프(신경망 구조)를 정의한다.

• C의 경우, 이웃이 많기 때문에 wide하지만 D는 이웃이 상대적으로 적으므로 구조가 더 좁다.
• E와 F는 그들의 이웃, 그리고 이웃들의 이웃 개수가 같기 때문에 구조가 같다. (다른 노드의 구조가 같을 수 있는 가능성을 보여줌)

Neighborhood aggregation

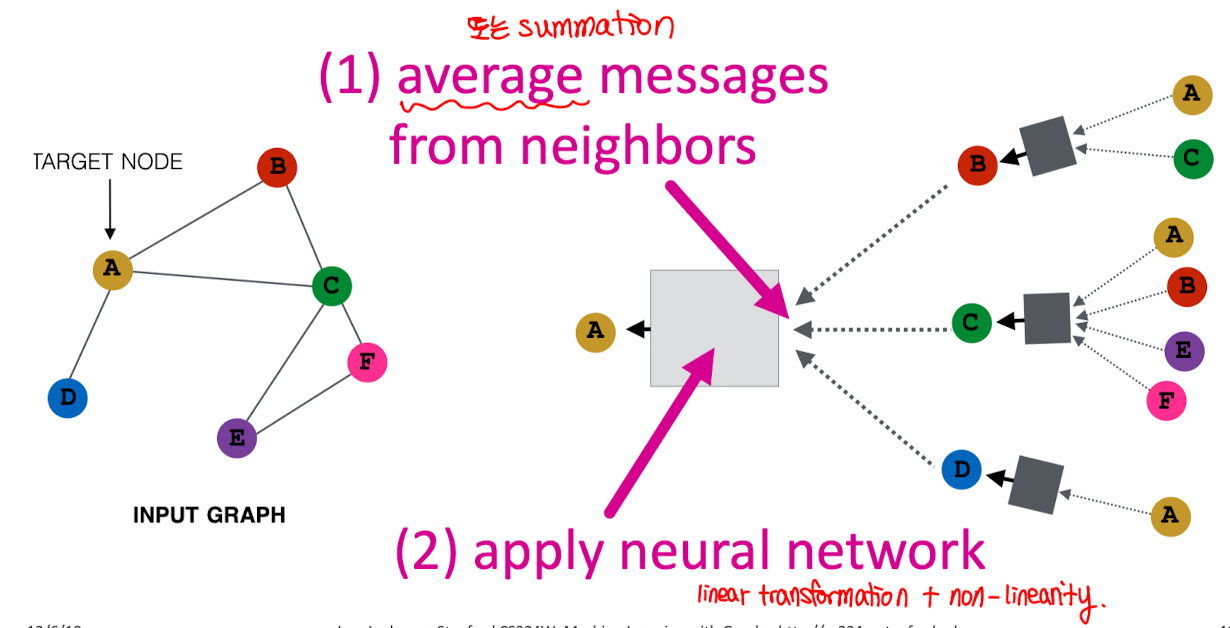
Deep Encoder

Shallow Encoder와는 반대되는 개념.

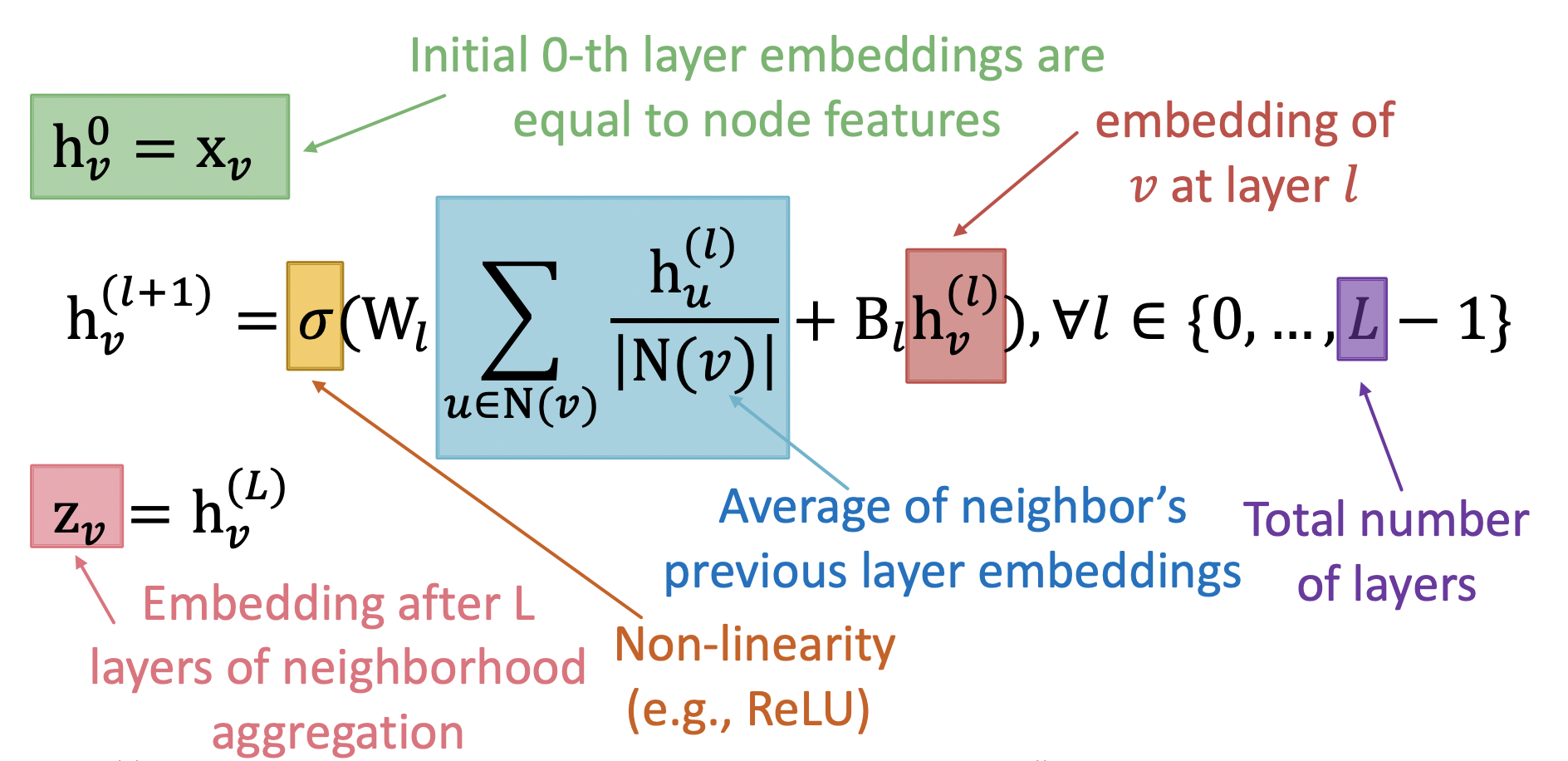
1. $h_v^0 = x_v$

• 0번째 레이어 임베딩 초기값 = 노드 특성과 동일

2. $h_v^{(l+1)} = \sigma(W_l\sum_{u\in N(v)}\frac{h_u^{(l)}}{|N(v)|}+B_lh_v^{(l)}),~~\forall ~l\in\{0,...,L-1\}$

• $\sum_{u\in N(v)}\frac{h_u^{(l)}}{|N(v)|}$: 이웃들의 이전 layer 임베딩 값들의 평균
• $h_v^{(l)}$: layer l의 v 노드에 대한 임베딩 (이전 layer) ⇒ 메시지. (5강. message passing 개념과 같이 살펴보기)
• L: layer의 총 개수. L번만큼 은닉층 값 계산 진행
• $\sigma$: 비선형성

3. $z_v = h_v^{(L)}$

• L개의 레이어의 neighborhood aggregation 이후의 임베딩 값

모델 훈련

학습되는 파라미터는 $W_l, B_l$ ⇒ 가중치 행렬

매 레이어마다 다른 파라미터를 지니지만 각 레이어에 있는 모든 노드에게는 해당 가중치 행렬들이 동일하게 적용된다.

이 임베딩 값들을 손실함수에 넣고 SGD를 돌려 가중치 파라미터를 학습시킨다.

행렬 계산(Matrix Formulation)

• $H^{(l)}=[h_1^{(l)}~...h_{|V|}^{(l)}]^T$ : 각 노드마다의 hidden 임베딩 값
• $\sum_{u\in N_v}h_u^{(l)} = A_{v,:}H^{(l)}$ : 그러면 인접행렬을 곱했을 때 각 노드마다 그들의 실제 이웃노드들만 값이 남음
• 대각행렬 D 정의 $D_{v,v} = Deg(v) = |N(v)|$
  • D의 대각 entries는 노드 v의 degree (이웃 개수)
  • D를 inverse해도 똑같이 대각행렬. $D_{v,v}^{-1} = 1/|N(v)|$

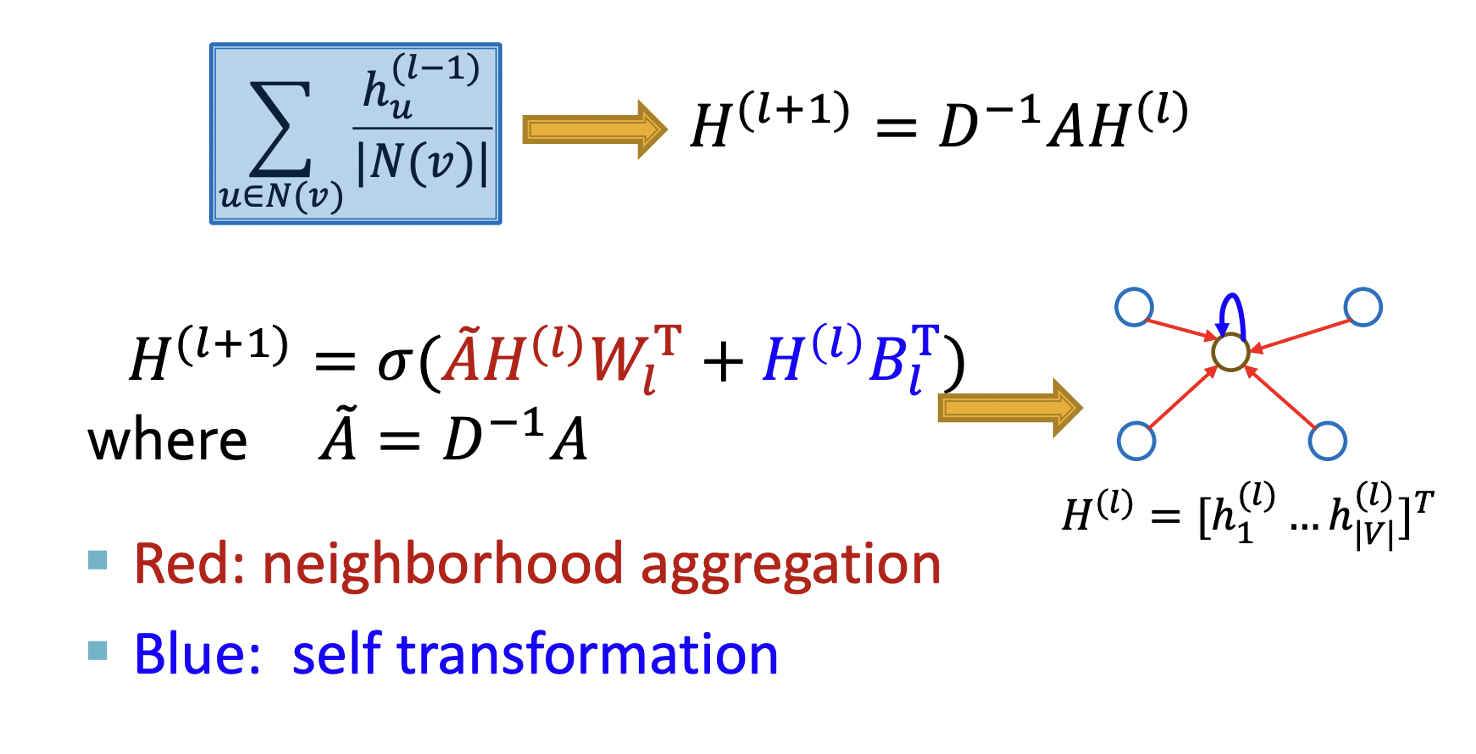
• 실제로는 인접행렬의 Normalized 버전으로 $\tilde A:=D^{-1/2}AD^{1/2}$ 를 사용하는 경우도 많다.
  • Graph Laplacian 개념

실제로 문제를 풀 때는 효과적으로 행렬곱을 이용할 수있음.

Note: 모든 GNN들이 행렬 형태로 표현될 수 있는 건 아님. (aggregation function이 복잡하면 그럴 수 있음)

모델 훈련 방법

Unsupervised Training

그래프의 구조를 supervision으로 사용함. 유사도 개념을 정의하고 노드 임베딩을 얻기 위해 deep encoder 사용 ⇒ “비슷한 노드는 비슷한 임베딩을 가진다.”

• 노드 u와 v가 비슷하면 $y_{u,v} = 1$
• CE는 Cross Entropy Loss (이진분류에 사용)
• DEC는 내적과 같은 decoder

노드 유사도는 lecture 3에 있는 개념 아무거나 가능

• Random walks(node2vec, DeepWalk), Matrix factorization, Node proximity in the graph …
• Lecture 3 정리글 참고

Supervised Training

downstream task 수행을 위해 모델을 직접 학습한다. (ex. 노드 분류)

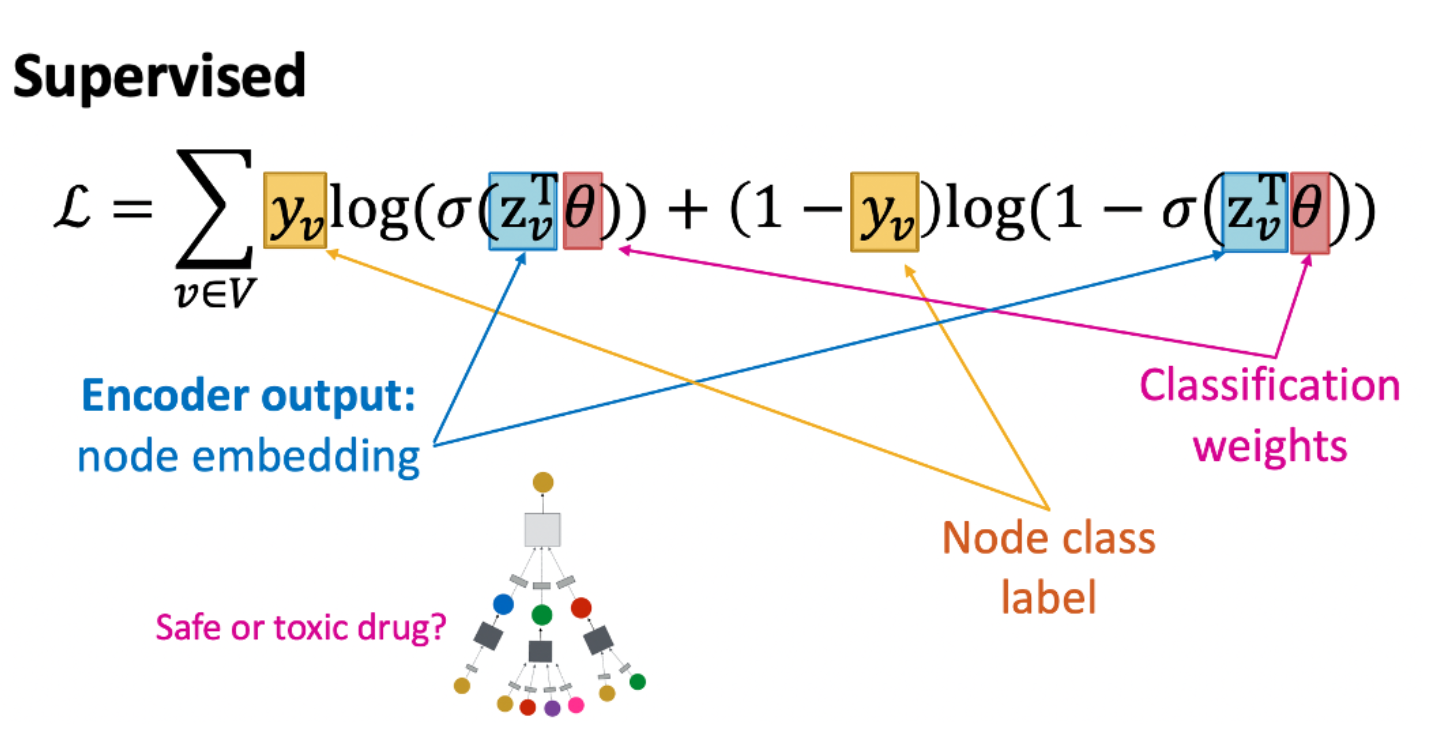
• $y_v$: 0이면 Safe, 1이면 Toxic
• $z_v^T$: 인코더 결과값. prediction.
• Θ: 분류 weight

Model Design: Overview

1. neighborhood aggregation 함수를 정의한다.
2. 임베딩에서의 손실 함수를 정의한다.
3. 노드 집합들에 대해서 훈련을 진행한다.
4. 필요한 만큼 노드에 대한 임베딩 벡터를 만든다. (우리가 훈련하지 않은 노드들에 대해서도 단순히 순전파를 통해 적용 가능)

Inductive Capability

똑같은 aggregation 파라미터들이 모든 노드에 대해 똑같이 적용된다. 모델 파라미터 개수는 네트워크 크기 |V|만큼 선형적이다. ⇒ 우리가 학습할 때 쓰지 않은 노드에 대해서도 일반화가 가능하다.

⇒ Generalize to entirely unseen graphs

⇒ 새로운 노드 또는 그래프가 나타나도 재학습할 필요가 없다.

3. GraphSAGE

Idea (1): 메시지 패싱 구조가 어떻게 다른가?

GraphSAGE는 Aggregation 함수를 flexible하게 지정할 수 있도록 한다.

함수 AGG는 이웃 노드의 feature 벡터 집합을 하나의 벡터로 보내는 임의의 미분가능한 함수로 족하다.

Idea (2): 모든 레이어에 있는 $h_v^{(l+1)}$ 임베딩에 L2 정규화를 취한다.

• L2 정규화가 없으면 각 벡터마다 다른 스케일의 임베딩 벡터를 얻게 됨.
• 몇몇 케이스에서는 정규화가 성능 향상에 도움을 줌.
• 정규화 이후에는 모든 벡터가 똑같은 L2 norm을 갖게 됨.

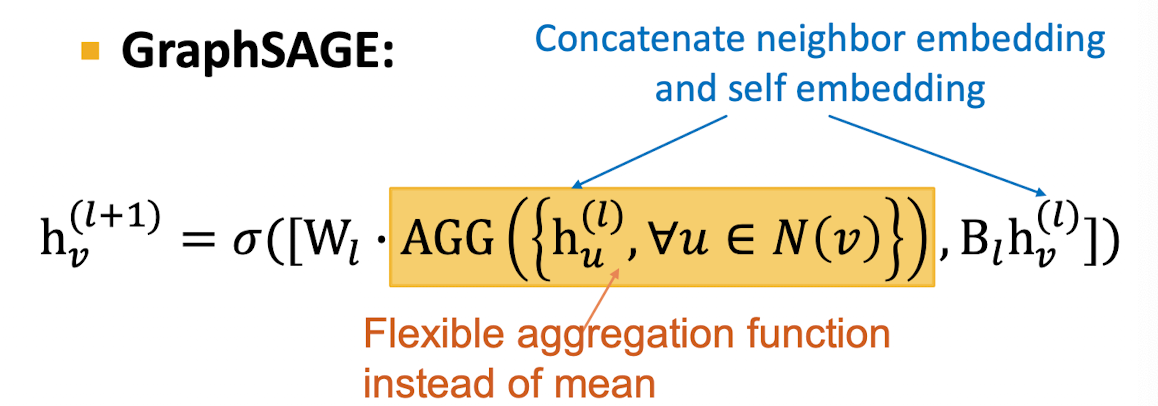
단순하게 다 더하고 이웃 노드 개수로 나눠서 정규화하지 않고 좀 더 flexible하게 AGG 함수를 지정할 수 있음. + 이웃 임베딩과 본인 임베딩 벡터를 concat

• [Mean] 이웃의 가중평균을 취함 (일반 neighbor aggregation과 같음)

• [Pool] 이웃 벡터를 변환한 후, symmetric vector function을 적용한다. element-wise하게 평균을 가져오든, 최댓값을 가져오는 함수. (CNN 3*3 pooling처럼)

• [LSTM] Reshuffled Neighbors에 대해 LSTM을 수행한다.