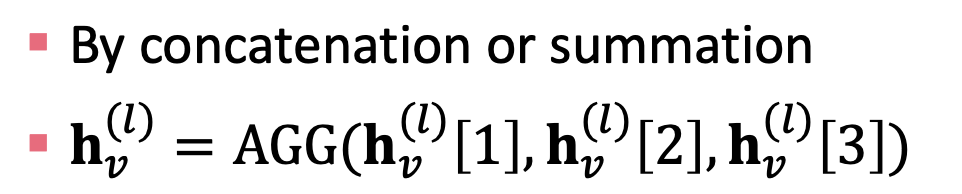일반적인 GNN 프레임워크
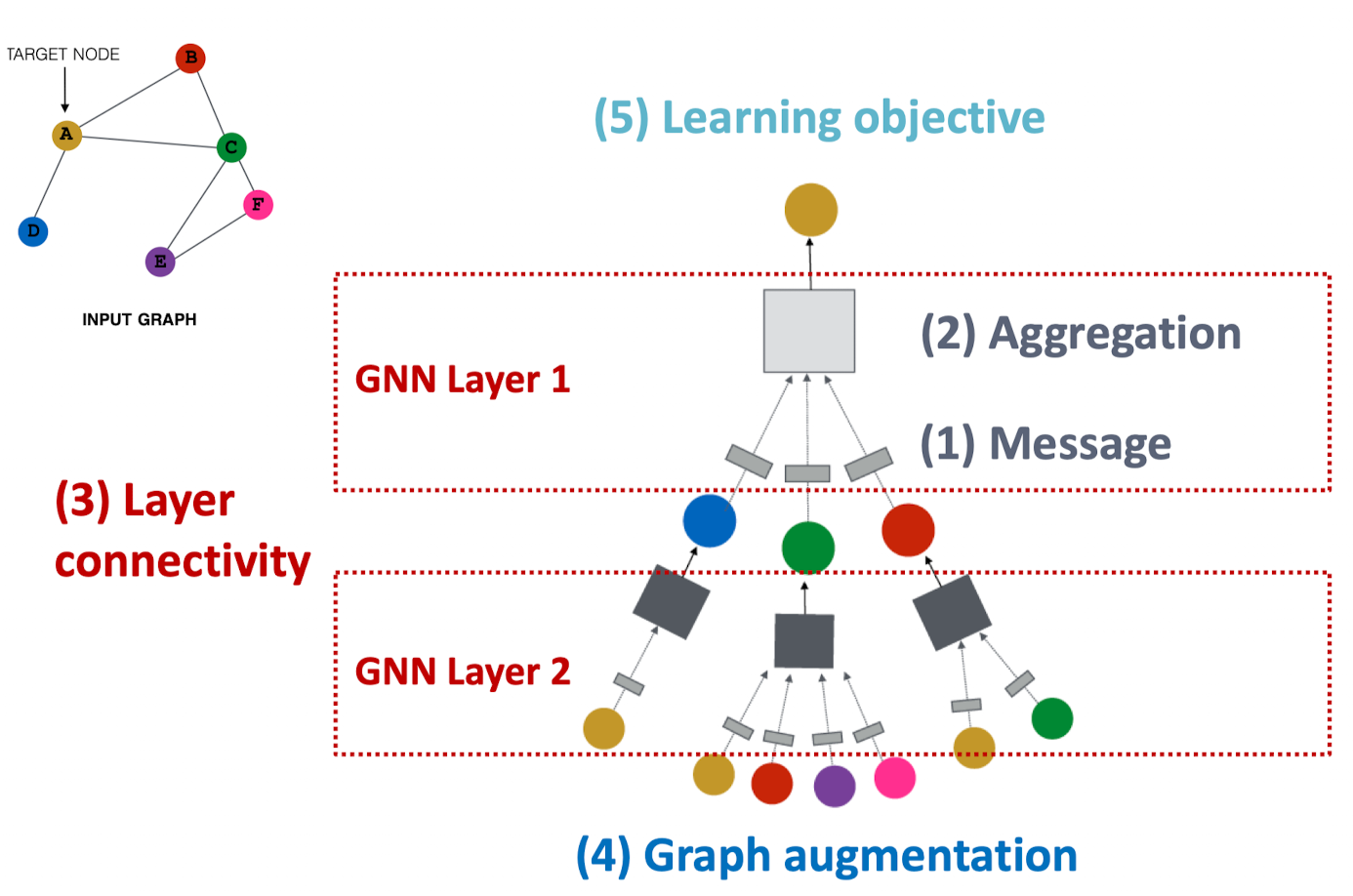
(1) (2) GNN Layer = 메시지 내용 + 집계(Aggregation) 방법
- 해당 내용의 변화에 따라 GNN의 인스턴트도 다양하게 나타남 (GCN, GraphSAGE, GAT, …)
(3) Layer Connectivity: GNN 레이어끼리 어떻게 연결할 것인가?
- 그대로 쌓는다 (Stack) vs. Residual Connection (Skip)
(4) Graph Augmentation: 일반 입력 그래프와 계산된 그래프끼리는 차이가 있다. 그래프의 feature 또는 구조에 대한 증강이 있다.
(5) 목적 함수 학습: 어떻게 GNN을 학습시킬 것인가?
- 지도/비지도학습
- 노드/엣지/그래프 수준의 목적 함수 → 다양한 task들이 존재
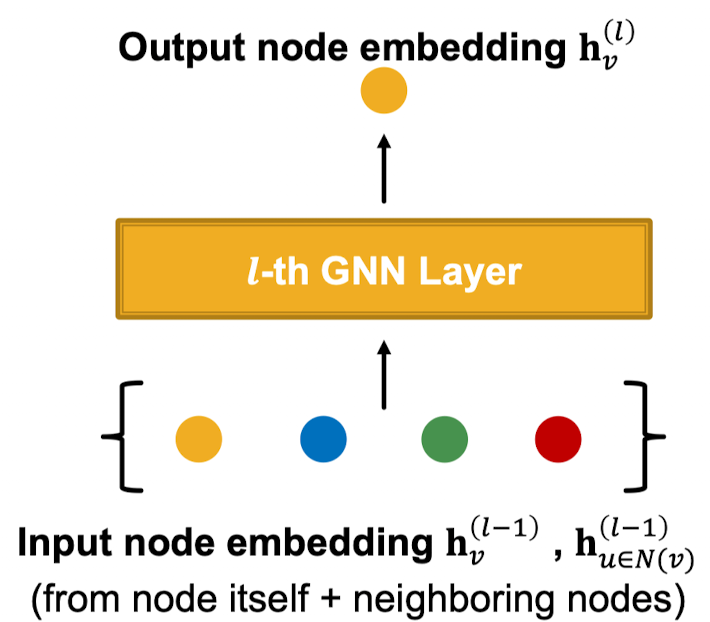
A Single Layer of a GNN
GNN Layer의 아이디어:
- 벡터의 집합을 하나의 벡터로 압축시킨다.
- 2가지의 과정을 거침
- (1) Message
- (2) Aggregation
(1) Message 계산
메시지 함수 :
- 직관: 각 노드는 메시지를 만드는데 이는 나중에 다른 노드들로 전달된다.
- 예시: 선형 레이어
- 가중치 행렬 를 노드 피쳐들과 곱해준다.
(2) Aggregation
- 직관: 각 노드는 노드 v의 이웃들로부터 메시지를 받아 집계될 것이다.
- 예시: Sum(⋅), Mean(⋅), Max(⋅) 집계 함수
문제점: 노드 v 스스로의 정보가 없어질 수 있다.
- 의 계산이 직접적으로 에 의존하지 않는다.
해결책: 을 계산할 때 을 포함시키자.
- (1) Message: 노드 v 스스로를 포함시켜서 메시지를 계산한다.
- 주로 이웃들과는 다른 계산 방법이 쓰일 것이다.
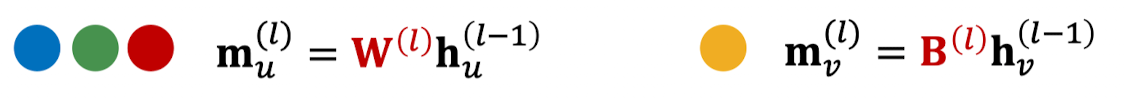
- 주로 이웃들과는 다른 계산 방법이 쓰일 것이다.
- (2) Aggregation: 이웃들을 집계한 후에 노드 v 자체의 메시지를 집계할 수 있다. (concat 또는 summation 사용)
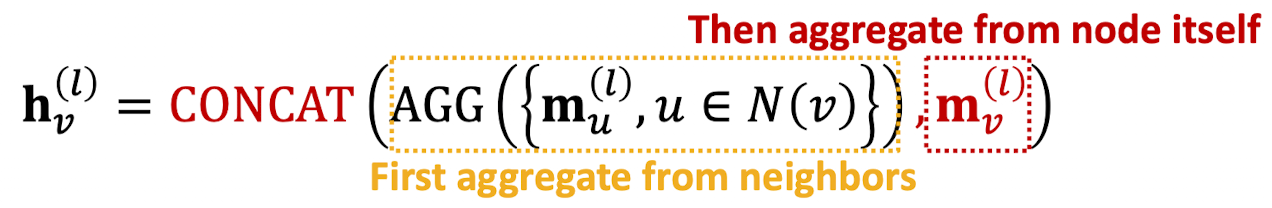
** 비선형성(활성화): 표현력(expression power)을 추가한다.
- 주로 시그모이드, ReLU 함수 등이 쓰인다.
- 메시지나 집계에 추가될 수 있다.
Classical GNN Layers: Graph Convolutional Networks(GCN)
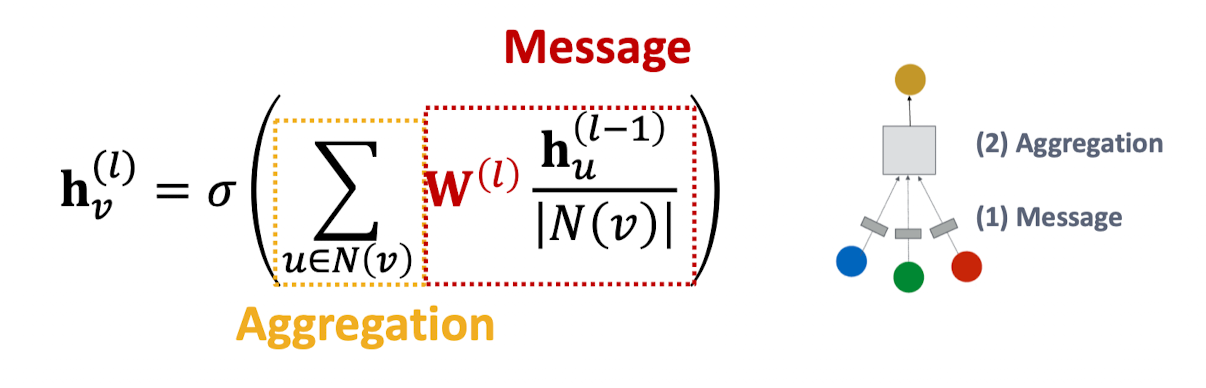
- 메시지(message)
- 각 이웃:
- 노드 degree에 의해 정규화됨 (실제 논문에서는 살짝 다른 정규화 방법을 사용함)
- 집계(aggregation)
-
이웃들로부터 메시지를 모아 모두 더하고, 활성화 함수를 적용한다.
-
Classical GNN Layers: GraphSAGE
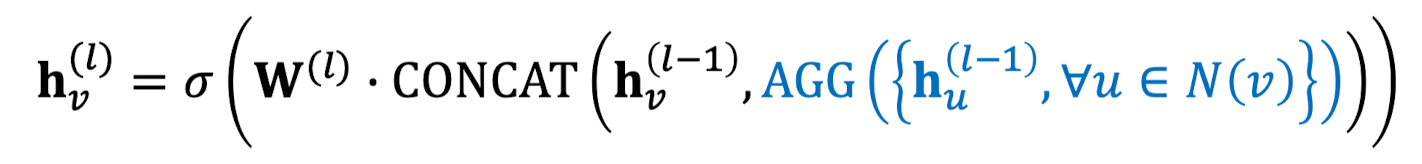
-
메시지: AGG 파란 부분.
-
2단계의 집계
- Stage 1: 노드 이웃들 집계
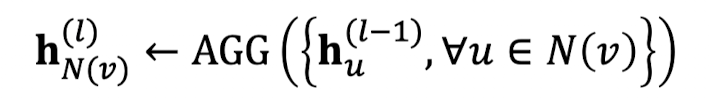
- Stage 2: 노드 스스로에 대한 집계를 추가로 진행 (을 stage 1 결과와 concat으로 붙임)
- Stage 1: 노드 이웃들 집계
GraphSAGE Neighbor Aggregation 방법
Mean: 노드의 가중평균을 둔다.
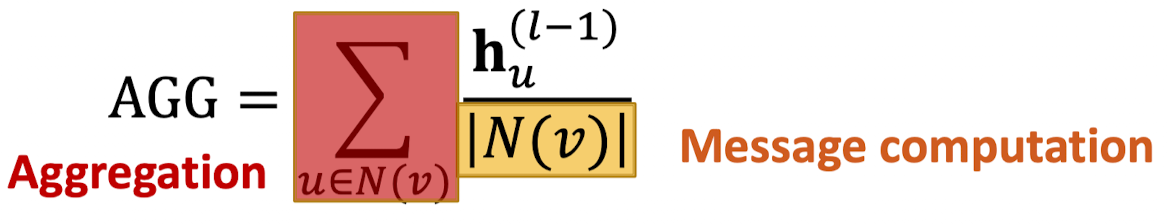
Pool: 이웃 벡터들을 변환시키고 Mean이나 Max로 symmetric 벡터 함수를 적용한다.
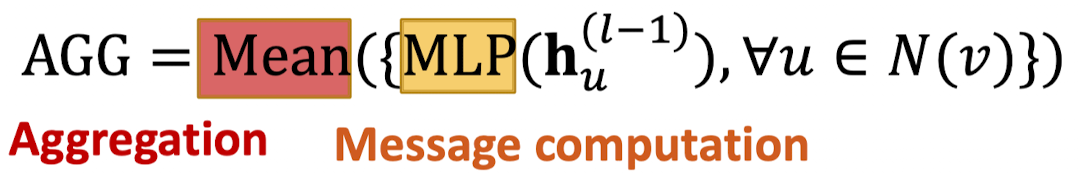
-
그저 선형 Layer가 아닌 MLP을 써서 메시지 계산을 할 수 있음.
-
다른 Aggregation 방법들은 다른 이론적인 특성들이 있음. 어떤 상황에서 어떤 집계 함수를 쓰는 게 좋을지가 다름.
LSTM: 다시 셔플된 이웃들에 LSTM(sequence model)을 적용한다.
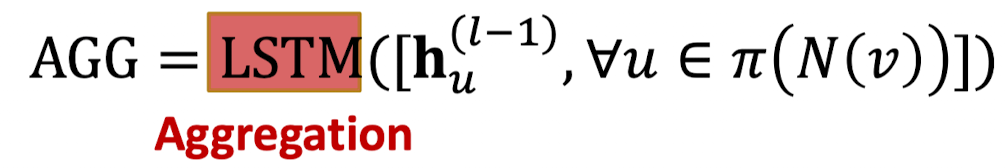
- 순서를 그대로 유지하는 함수가 . sequence 모델의 경우 입력이 들어간 순서대로 다시 나와야 하기 때문에 유지해주는 것이 필요하다.
L2 정규화 (Optional)
모든 레이어에서 에 L2 정규화를 진행한다.
where -norm)
- 정규화가 없으면 임베딩 벡터는 다른 스케일을 가지게 된다.
- 몇몇 케이스들에서는 임베딩 벡터의 정규화가 성능 향상의 결과를 가져온다.
- 정규화 이후에는 모든 벡터들이 동일한 L2 norm을 갖게 될 것이다.
Classical GNN Layers: Graph Attention Networks(GAT)

- GCN, GraphSAGE에서는
- 가 노드 v로 가는 노드 u의 가중치 요소(중요도)
⇒ 가중치 요소가 그래프의 구조적 특성에 기반해 명시적으로 정의되어 있다. (노드 degree)
⇒ 모든 이웃노드 u가 노드 v에 대해 똑같이 중요하다.
- 가 노드 v로 가는 노드 u의 가중치 요소(중요도)
- 그러나 모든 이웃 노드들이 동일하게 중요하진 않다.
- attention 는 입력 데이터 중 중요한 부분들에 더 집중하고 나머지는 사라지게 한다.
- 신경망은 작지만 중요한 부분의 데이터에 더 많은 계산을 쏟아야 한다.
- 어느 데이터가 더 중요하냐?는 맥락에 의존하고 학습을 통해 배울 수 있다.
❓ 단순한 이웃 집계보다 더 나은 성과를 보이는가?
❓가중치 요소가 학습되게끔 만들 수 있는가?
Goal: 그래프의 각 노드의 다른 이웃들에 임의적인 중요성을 특정짓는다.
Idea: attention 전략을 통해 각 노드 임베딩 벡터 를 계산한다.
(1) Attention 계수 계산
** = 노드 v로 가는 노드 u의 메시지의 중요도
(2) 를 정규화하여 최종 attention 가중치 계산 (softmax)
(3) 최종 attention 가중치에 기반하여 가중합 진행

- 어텐션 메커니즘은 무엇을 선택하든 상관없다
- simple single-layer neural network: 선형 layer에 가중치가 훈련가능한 파라미터로 존재함.
- 어텐션 가중치 파라미터들은 함께 훈련된다
- 처음부터 끝까지 신경망에 있는 다른 파라미터들()과 함께 훈련시킨다.
💡 Multi-head Attention: 어텐션 메커니즘의 훈련 과정을 안정화시킨다.
는 잘 수렴하지 않기 때문에, 해당 매커니즘을 안정화 하기 위해 여러 개의 attention score를 사용한 뒤 concat하거나 sum하여 최종 임베딩 벡터를 구함.
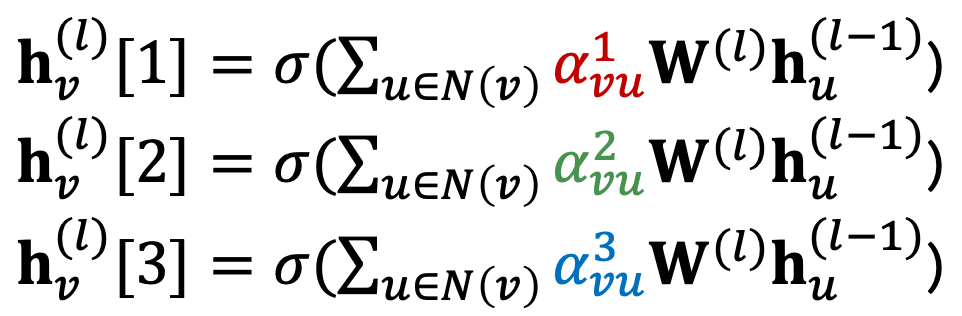
어텐션 메커니즘의 이점
💡 다른 이웃들에 대해 다른 중요도 가치()를 특정할 수 있도록 한다.
- Computationally efficient: 어텐션 계수는 그래프의 모든 엣지들에 걸쳐 병렬 방식으로 계산할 수 있다. Aggregation 또한 모든 노드들을 걸쳐 병렬적으로 계산 가능하다.
- 저장공간 효율성: 희소 행렬 방식은 O(V+E)만큼의 entries만 사용된다.
- 국소적인 방식(Localized): local한 네트워크 이웃들에서만 어텐션 점수를 계산할 수 있다.
- 귀납(inductive) 가능성: edge-wise한 메커니즘과 공유된다. 글로벌한 그래프 구조에 의존하지 않는다.
GNN Layer in Practice
일반적인 GNN 레이어 디자인을 고려하자. ⇒ 현대 딥러닝 모듈을 포함시키기.
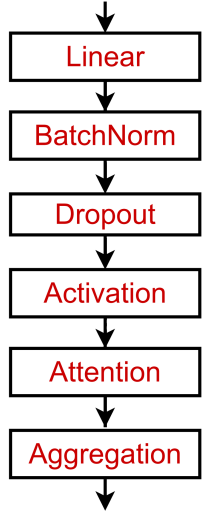
Batch Normalization(배치 정규화)
목표: 신경망 학습 안정화
아이디어: 입력의 배치(node embeddings)가 주어졌을 때
- 노드 임베딩 벡터들의 평균을 0으로 맞춘다.
- 분산을 unit variance로 다시 스케일링 한다.
Dropout(드롭아옷)
목표: 오버피팅 방지를 위한 신경망 정규화
아이디어:
- 훈련중: p의 확률로 랜덤하게 뉴런을 0으로 세팅(turn off)
- test중: 모든 뉴런을 계산에 사용
GNN에서는 message 함수에서의 선형 레이어에 적용된다.
활성화 함수(비선형성)
임베딩 x의 i번째 차원에 활성화 함수를 매번 적용한다.
- ReLU, Sigmoid,
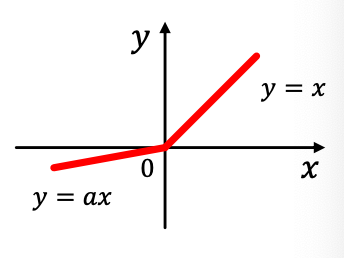
- Parametric ReLU(PReLU):
- 여기서 는 훈련 가능한 파라미터
- 경험적으로 ReLU보다 더 좋은 성능을 지님.
(3) Stacking Layers of a GNN (Layer connectivity)
Over-smoothing Problem
GNN 레이어를 많이 쌓으면 생기는 문제점. 모든 임베딩이 똑같은 값으로 수렴한다.
- Receptive field(수용 영역): 내가 관심 있는 노드의 임베딩을 결정하는 노드들의 집합
- K-layer GNN에서는 각 노드는 K-hop 이웃들의 수용 영역을 가지고 있다.
- hop의 수를 늘릴수록 공유되는 이웃들의 개수가 빠르게 늘어난다.
- 만약 특정 2개의 노드가 공유하는 이웃들이 많이 겹친다면, 임베딩도 매우 비슷할 것이다.
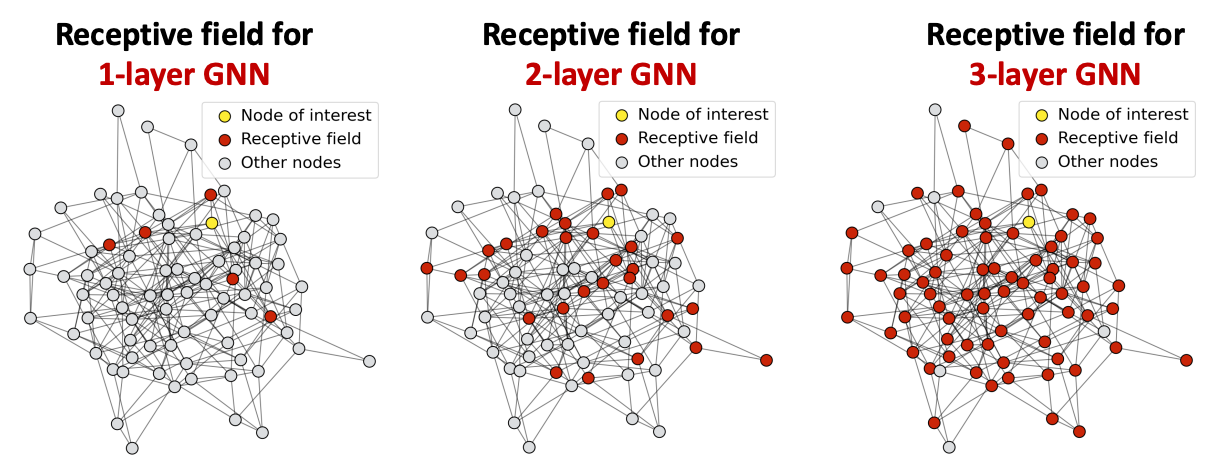
💡 GNN 레이어를 많이 쌓는다 ⇒ 노드들의 수용 영역이 많이 겹친다 ⇒ 노드 임베딩이 많이 비슷해진다 ⇒ over-smoothing problem
Expressive Power for Shallow GNNs
Lesson 1: GNN 레이어를 쌓을 때 조심해야 한다!
- CNN과 같은 다른 신경망들과는 달리 GNN 레이어를 많이 쌓는다고 항상 도움되는 건 아니다.
- Step 1: 문제를 해결하는데 필요한 수용 영역을 분석해라 (ex. 그래프의 지름 계산하기)
- Step 2: 레이어 개수를 불필요하게 많이 잡을 필요가 없다. 우리가 원하는 수용 영역보다 조금 더 큰 GNN 레이어 L을 설정해라.
GNN 레이어 수가 적은 신경망의 expressive power를 높이는 방법은?
1. 각 GNN 레이어 자체의 expressive power를 높여라.
메시지 제작 및 전달 과정에서 Aggregation / Transformation 레이어를 더 깊은 신경망으로 만든다.
2. GNN 레이어 앞뒤로 메시지를 전달하지 않는 MLP 레이어를 추가해라.

Pre-processing layers: 인코딩 노드 특성들이 필요할 때 중요하다. (ex. 노드가 이미지, 텍스트일 때)
Post-processing layers: 노드 임베딩에 대한 reasoning, transformation이 필요할 때 중요하다. (ex. 그래프 분류, 지식 그래프)
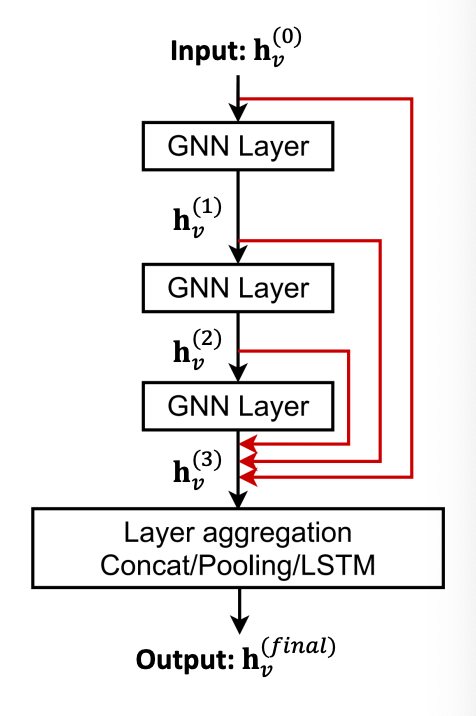
Skip Connections
그럼에도 불구하고 GNN 레이어를 많이 요구하는 경우가 있을 수 있음. 그럴 땐?
Lesson 2: GNN에 skip connection들을 추가해라.
- over-smoothing에서의 발견점: 가끔은 앞쪽 GNN 레이어에 있는 노드 임베딩 벡터들이 노드들을 더 잘 분류할 수 있음.
- Solution: GNN에 지름길(shortcut)을 추가해줌으로써 최종 노드 임베딩에 앞선 레이어의 영향력을 높일 수 있다.
Skip Connection의 작동 원리
- Skip Connection은 모델 혼합을 만들어준다.
- N개 skip connections → 개의 가능한 경로들
- shallow한 GNN과 deep한 GNN 모두를 가질 수 있다.
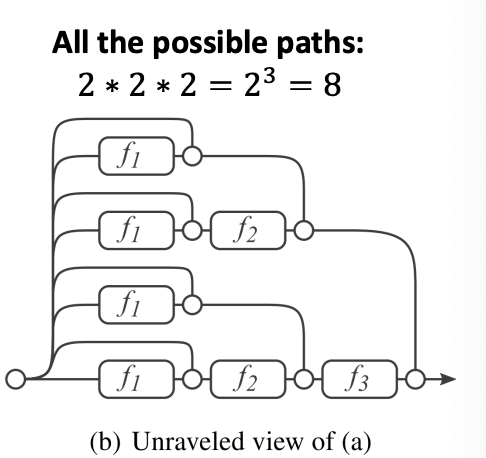
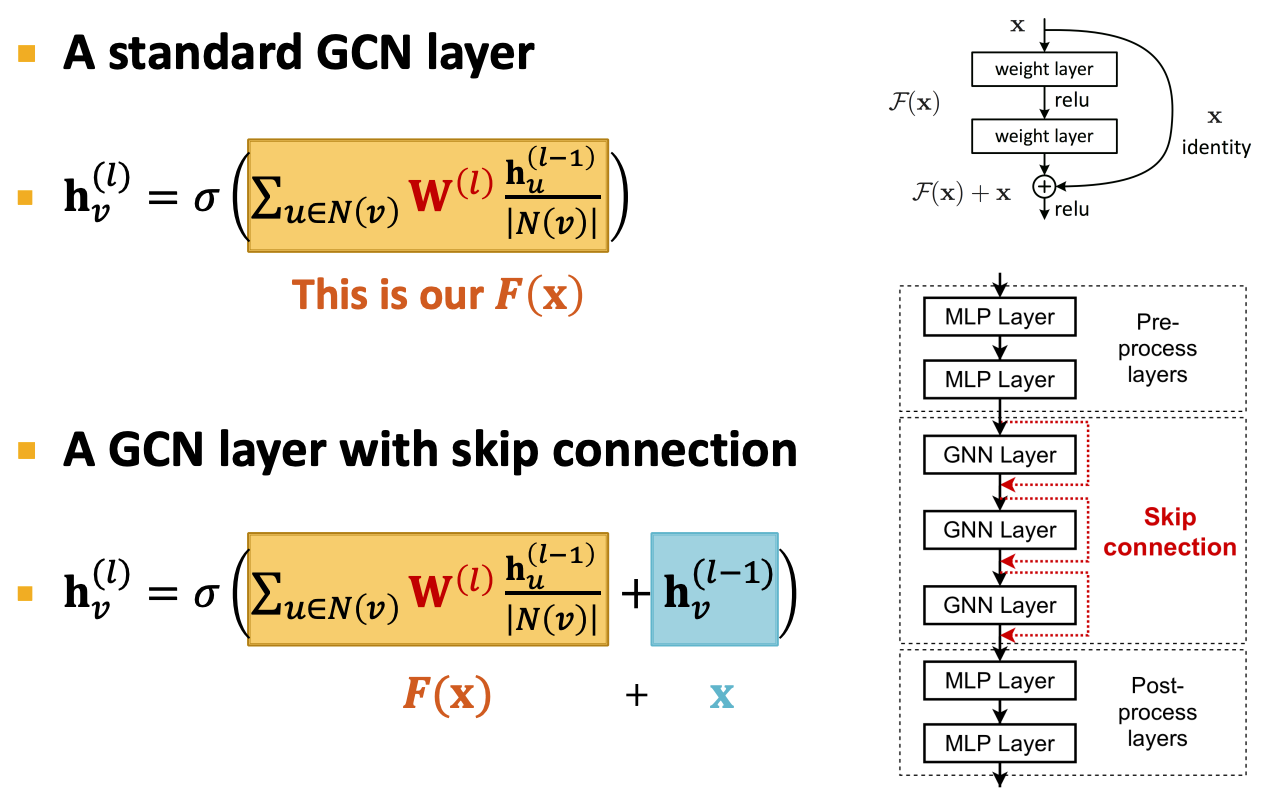
다른 옵션: 바로 마지막 레이어로 skip할 수 있도록 함. 마지막 레이어가 이전에 있는 모든 레이어의 노드 임베딩을 집계할 수 있도록.