
✔️비선형 회귀 분석
-
선형가정이 어긋나는(정규성 위배) dataset인 경우,
대처방법으로 다항식 항을 추가하여 다항회귀 모델을 작성한다. -
회귀선을 곡선으로 변환해 보다 더 정확히 데이터 변화를 예측하는데 그 목적이 있다.
선형으로 예측
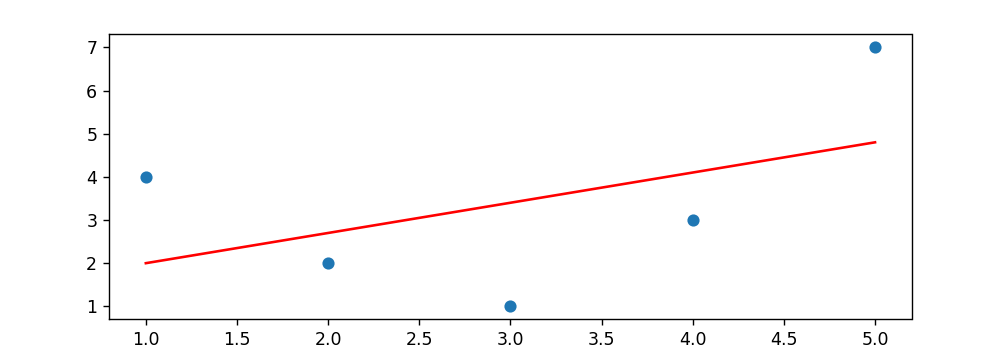
x = np.array([1,2,3,4,5])
y = np.array([4,2,1,3,7])
from sklearn.linear_model import LinearRegression
x = x[:,np.newaxis] #1->2차원확장
model = LinearRegression().fit(x,y)
ypred = model.predict(x)
print(ypred) #[2. 2.7 3.4 4.1 4.8]
plt.scatter(x,y)
plt.plot(x,ypred,c='red')
plt.show() #x가 y를 제대로 설명한다고 보기에 문제가 있다.2차원의 데이터를 예측한다면, 단순히 LinearRegression 만으로 모델을 생성하기에는 무리가 있다.
비선형 예측
- 이에 대한 해결방법은 독립변수를 추가해
다항식을 만드는 식으로 데이터를 변환해 모델에 유연성을 주면 된다.
from sklearn.preprocessing import PolynomialFeatures
ploy = PolynomialFeatures(degree=3,include_bias=False)
x2 = ploy.fit_transform(x) #특징행렬을 만듦
#특징행렬값으로 다시 학습
model2 = LinearRegression().fit(x2,y)
ypred2 = model2.predict(x2)
plt.scatter(x,y)
plt.plot(x,ypred2,c='red')
plt.show()
print(y) #실제
print(ypred2) #예측
# [4 2 1 3 7]
# [4.14 1.62 1.25 3.02 6.94]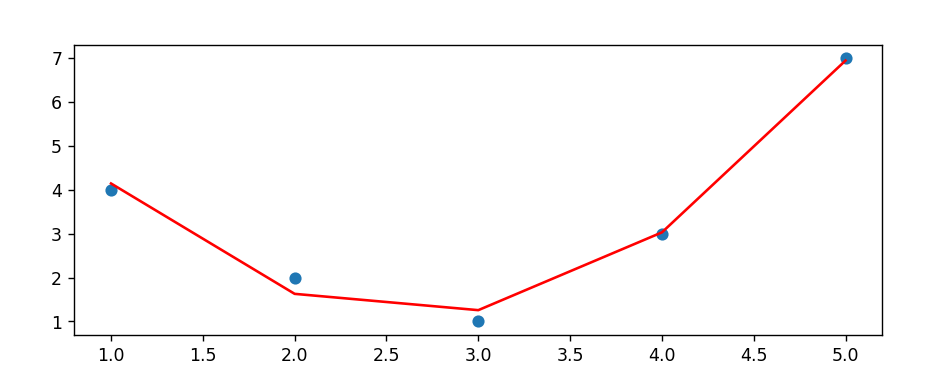
예측값과 실제값이 어느정도 일치하는것을 볼 수 있다.
PolynomialFeatures(degree): 열 개수.
높을수록 편차가 줄어들지만 너무 높게 줘도 over fitting의 문제가 발생한다
✏️예제
data information
보스턴 시의 주택 가격에 대한 데이터이다.
주택의 여러가진 요건들과 주택의 가격 정보가 포함되어 있다. 주택의 가격에 영향을 미치는 요소를 분석하고자 하는 목적으로 사용될 수 있다. 회귀분석 등의 분석에 활용될 수 있다.
데이터명 : Boston Housing Price (보스턴 주택 가격 데이터)
레코드수 : 506 개
필드개수 : 14 개
[01] CRIM 자치시(town) 별 1인당 범죄율
[02] ZN 25,000 평방피트를 초과하는 거주지역의 비율
[03] INDUS 비소매상업지역이 점유하고 있는 토지의 비율
[04] CHAS 찰스강에 대한 더미변수(강의 경계에 위치한 경우는 1, 아니면 0)
[05] NOX 10ppm 당 농축 일산화질소
[06] RM 주택 1가구당 평균 방의 개수
[07] AGE 1940년 이전에 건축된 소유주택의 비율
[08] DIS 5개의 보스턴 직업센터까지의 접근성 지수
[09] RAD 방사형 도로까지의 접근성 지수
[10] TAX 10,000 달러 당 재산세율
[11] PTRATIO 자치시(town)별 학생/교사 비율
[12] B 1000(Bk-0.63)^2, 여기서 Bk는 자치시별 흑인의 비율을 말함.
[13] LSTAT 모집단의 하위계층의 비율(%)
[14] MEDV 본인 소유의 주택가격(중앙값) (단위: $1,000)1️⃣ data load
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rc('font',family='malgun gothic')
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
df = pd.read_csv('../testdata/housing.data',header=None,sep='\s+')
df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS' ,'NOX', 'RM', 'AGE' ,'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
print(df.corr()) #LSTAT(독립), MEDV(종속) -0.73..- 참여변수 (음의 상관관계 -0.73)
LSTAT: 독립변수MEDV: 종속변수
2️⃣ data degree (2,3)
lstat = df[['LSTAT']].values
medv = df[['MEDV']].values
model = LinearRegression()
# 다항특성
quad = PolynomialFeatures(degree=2)
cubic = PolynomialFeatures(degree=3)
lstat_quad = quad.fit_transform(lstat)
lstat_cubic = cubic.fit_transform(lstat)- 비선형 분석을 위해 독립변수 LSTAT을 2차,3차로 나누어 가공했다.
lstat_quad: 하위계층의 비율(2차)lstat_cubic: 하위계층의 비율(3차)
비선형분석을 하기전에 먼저 단순회귀분석으로써 분석된 결정계수를 알아보자
3️⃣ LinearRegression
model.fit(lstat, medv)
lstat_fit = np.arange(lstat.min(), lstat.max(), 1)[:, np.newaxis] # 그래프 표시용
medv_lin_fit = model.predict(lstat_fit)
# 결정계수 0.544
model_r2 = r2_score(medv, model.predict(lstat))
print(model_r2)- 결정계수는 0.544가 나왔다. (54%)
4️⃣ Non-LinearRegression 2,3
# Non - LinearRegression 2차
model.fit(lstat_quad, medv)
medv_quad_fit = model.predict(quad.transform(lstat_fit))
q_r2 = r2_score(medv, model.predict(lstat_quad))
print(q_r2)
# Non - LinearRegression 3차
model.fit(lstat_cubic, medv)
medv_cubic_fit = model.predict(cubic.transform(lstat_fit))
c_r2 = r2_score(medv, model.predict(lstat_cubic))
print(c_r2) # 결정계수 0.657- 차수(degree)가 높을수록 결정계수가 높아진다.
- 2차 결정계수 : 0.640
- 3차 결정계수 : 0.657
👁️🗨️시각화
#시각화
plt.scatter(lstat,medv,c='lightgray',label='학습데이터')
#선형 그래프
plt.plot(lstat_fit,medv_lin_fit,linestyle=':',\
label='linear fit(d=1), $R^2=%.2f$'%model_r2,c='b',lw=3)
#비선형그래프2
plt.plot(lstat_fit,medv_quad_fit,linestyle='-',\
label='quad fit(d=2), $R^2=%.2f$'%q_r2,c='r',lw=3)
#비선형그래프3
plt.plot(lstat_fit,medv_cubic_fit,linestyle='--',\
label='cubic fit(d=3), $R^2=%.2f$'%c_r2,c='k',lw=3)
plt.xlabel('하위계층의 비율')
plt.ylabel('주택가격')
plt.legend()
plt.show()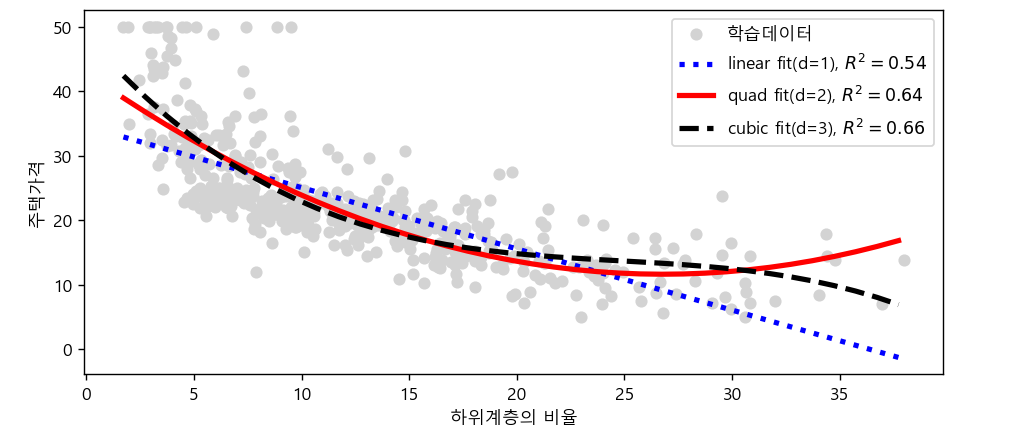
- ⛔주의
비선형모델이 무조건 좋은 것은 아니다.
원본데이터 재가공을 고민하는것도 방법이며,.
모델선택시 분석가의 경험, 능력이 중요
