로지스틱 회귀분석
-
종속변수와 독립변수 간의 관계로 예측모델을 생성한다는 점에서 선형회귀분석과 유사하다. 하지만 독립변수(x)에 의해 종속변수(y)의 범주로 분류한다는 측면에서 분류분석 방법이다.
-
분류 문제에서 선형 예측에 시그모이드 함수를 적용하여 가능한 각 불연속 라벨 값에 대한 확률을 생성하는 모델로,
이진분류 문제에 흔히 사용되지만 다중클래스 분류(다중 클래스 로지스틱 회귀 또는 다항회귀 )에도 사용될 수 있다.
특징
- 종속변수는 범주형이다. (이항형 : Yes/No 또는 다항형 : 예 - iris의 Spices 칼럼)
- 정규성 : 정규분포 대신에 이항분포(성공확률이 P인 n회의 베르누이 독립시행) 를 따른다
- 로짓변환 : 종속변수의 출력범위를 0과 1로 조정하는 과정을 의미한다.
- 활용분야 : 의료, 통신, 날씨 등 분류를 목적으로 다양한 분야에서 활용된다.
로지스틱 회귀분석은 종속변수(y 결과변수)가 범주형 데이터인 경우에 사용되는 기법으로 예측하고자 하는 것이 수치화 하기 힘든 변수,
예를 들어 어떤 고객이 부도를 낼 것인지의 여부, 타이타닉호에서의
생존 여부, 개인별 최종학력 알기 등의 경우에 사용할 수 있다.
odds
Odds는 성공 확률이 실행 확률에 비해 몇 배 더 높은 가를 나타낸다.
-
Odds :
P / (1-P)(성공률/실패율)0=< P(x) =<100 0 10 50 90 100 0 < odds < ∞ 0 0.11 1 9 ∞

-
odds ratio 수식에서 log를 씌우면 로짓변환이 가능.
-
로짓변환(Logit function) : Odds에 로그를 취한 함수로써 입력값의
범위가 [-∞ , +∞]일 때 출력 값의 범위를 [0, 1]]로 조정한다.
이는 이항분류시에서 시그모이드 함수를 사용한 정규화와 유사하다. (0~0.5는 0. / 0.5~1은 1)
🔗odds에 대해
🔗활성함수(Activation) 시그모이드(Sigmoid)함수 정의
분류모델 예제1
방법1 statsmodels
- mtcars의 mpg 연비 ,hp 마력 독립변수를 이용하여 범주형인 am(수동/자동)을 분류해보자
import statsmodels.api as sm
mtcars = sm.datasets.get_rdataset('mtcars').data
mtcar = mtcars.loc[:,['mpg','hp','am']]
#연비와 마력수에 따른 변속기 분류(수동,자동)
import statsmodels.formula.api as smf
formula = 'am ~ hp + mpg'
result = smf.logit(formula=formula,data=mtcar).fit()
print(result.summary())-
am 을 종속변수로, hp,mpg를 독립변수로 사용하고,
statsmodels의logit함수로 로짓변환하여 학습시킨다. -
Logit Regression Results
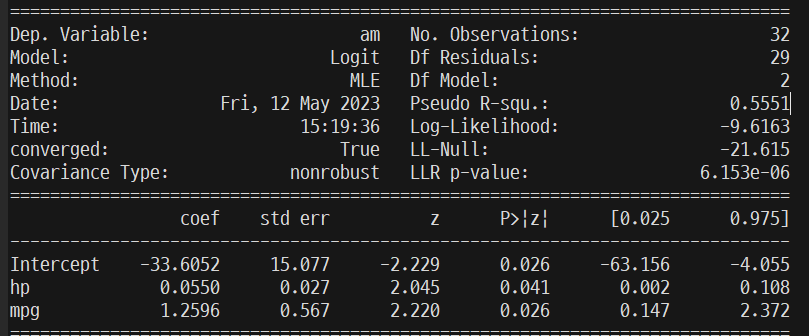
-
P>|z|: 0.05 아래이므로 유의미한 분석이다.
이제 예측. 실제값과 비교를 해보자
import numpy as np
pred = result.predict(mtcar[:10])
print('예측값', pred.values) #0.25 0.25 0.558 0.355 0.397 0.006
print('예측값', np.around(pred.values)) ##0.5를 기준으로 분류 (0/1)
print('실제값', mtcar['am'][:10].values)
'''
예측값 [0. 0. 1. 0. 0. 0. 0. 1. 1. 0.]
실제값 [1 1 1 0 0 0 0 0 0 0]
'''- 분류 정확도가 조금 떨어지지만 분류를 성공했다.
confusion matrix
빈도표로 분류정확도를 계산해보자
conf_tab = result.pred_table()
print('confusion matrix: \n',conf_tab) #빈도표
# 1 0
#1 [16. 3.]
#0 [ 3. 10.]
#분류정확도
print((conf_tab[0][0]+conf_tab[1][1]) / len(mtcar))- 0.81 accuracy : 분류 정확도가 81%로 도출되었다.
방법2 glm
- General linear model : 일반화된 선형모델
- 이항분류시 Binomial 함수를 사용한다.
result2 = smf.glm(formula='am ~ hp + mpg', data=mtcar,family=sm.families.Binomial()).fit()
print(result2.summary())
glm_pred = result2.predict(mtcar[:10])
print('예측값', np.around(glm_pred.values)) #예측값
print('실제값', mtcar['am'][:10].values) # 실제값분류정확도
- accuracy_score : 분류정확도를 확인하는 함수
- 실제값,예측값 순서로 파라미터를 지정한다.
from sklearn.metrics import accuracy_score
glm_pred2 = result2.predict(mtcar)
print(accuracy_score(mtcar['am'],np.around(glm_pred2.values))) # 0.812
# 새로운 값에 대한 예측
import pandas as pd
newdf = pd.DataFrame({'mpg':[10,30,50,5],'hp':[80,100,130,50]})
new_pred = result2.predict(newdf)
print(np.around(new_pred.values)) #[0. 1. 1. 0.]각각 두 값에 대한 예측된 am의 분류 결과를 출력했다.
- ML 의 포용성(inclusion,tolerance) : 과적합이 발생하지 않은 상태에서 최적의 모델을 생성한다.
최적화 / 일반화의 적절함이 중요.
분류모델 예제2
문1] 소득 수준에 따른 외식 성향을 나타내고 있다.
주말 저녁에 외식을 하면 1, 외식을 하지 않으면 0으로 처리되었다.
다음 데이터에 대하여 소득 수준이 외식에 영향을 미치는지 로지스틱 회귀분석을 실시하라.
키보드로 소득 수준(양의 정수)을 입력하면 외식 여부 분류 결과 출력하라# 학습
model = smf.glm(formula='외식유무 ~ 소득수준',data=mydata,family=sm.families.Binomial()).fit()
print(model.summary())
pred = model.predict(mydata)
# 분류정확도
from sklearn.metrics import accuracy_score
print(accuracy_score(mydata['외식유무'],np.around(pred))) #0.904
# 새 데이터 입력 예측
new_input_data = pd.DataFrame({'소득수준':[int(input('소득수준 입력'))]})
flag = np.rint(model.predict(new_input_data))[0] # 0 외식안함 / 1 외식함
print('외식함' if flag == 1 else '외식안함')