선형회귀분석

kangjuju·2023년 5월 10일
formulalinear_regressionlinregressmake_regressionolspredict기계학습회귀분석
0

회귀분석

목록 보기
2/11

✔️기계학습

머신러닝은 학습하려는 문제의 유형에 따라 크게 다음과 같은 세 가지로 분류할 수 있다.

  1. 지도 학습(Supervised Learning)
    • 여러 문제와 답을 같이 학습함으로써 미지의 문제에 대한 올바른 답을 예측한다.
    • 예측 / 추정 : 분류 모델과는 달리 레이블이 달린 학습 데이터를 가지고
      특징(feature)과 레이블(label) 사이의 상관관계를 함수식으로 표현
    • 분류 : 레이블이 달린 학습 데이터로 학습한 후에
      새로 입력된 데이터가 학습했던 어느 그룹에 속하는 지를 찾아내는 방법
  1. 비지도 학습(Unsupervised Learning)
    • 패턴/구조발견
    • 그룹화
    • 차원 축소
    • 영상,이미지,문자
  2. 강화 학습(Reinforcement Learning)

✔️회귀분석

  • 상관관계 분석 : 변수 간의 관련성을 분석

  • 회귀분석

    • 변수 간의 인과관계를 분석하며, 사용범위가 넓은 분석방법이다.
    • 이는 변수 들의 관련성 규명을 위해 어떤 수학적 모형을 가정하고, 이 모형을 측정된 변수들의 데이터로부터 추정하는 통계방법이다.
    • 독립변수의 값에 의해 종속변수의 값을 예측할 수 있다.

  • 단순회귀분석

    • 독립변수와 종속변수가 각각 1개인 경우에 독립변수가 종속변수에 어떠한 영향을 미치는 가에 대한 인과관계를 분석.
      + 최적의 추세선을 구하기 위한 학습 (❗회귀계수)
  • 다중회귀분석
    여러 개의 독립변수로 1개의 종속변수에 미치는 영향 분석

❗회귀계수

  • 단순선형회귀모델에서 최소제곱법을 이용해 회귀계수를 구한다.
    이 회귀계수의 목적은 관찰된 자료를 가장 잘 표현하는 직선을 구하기 위함이다.
    (최적의 추세선)

  • 잔차 : 적합한 추세선과 실제 자료의 차이를 잔차라고한다. 여기서 모든 잔차의 합은 0인데, 회귀계수를 구하려면 잔차를 제곱(최소제곱법)하여 회귀계수를 구한다.

  • 잔차제곱의 합이 최소가 되는 것이 목표이며, 그 값을 구하려면 미분을 이용해야 한다. (y절편,기울기를 구하므로 편미분을 사용)

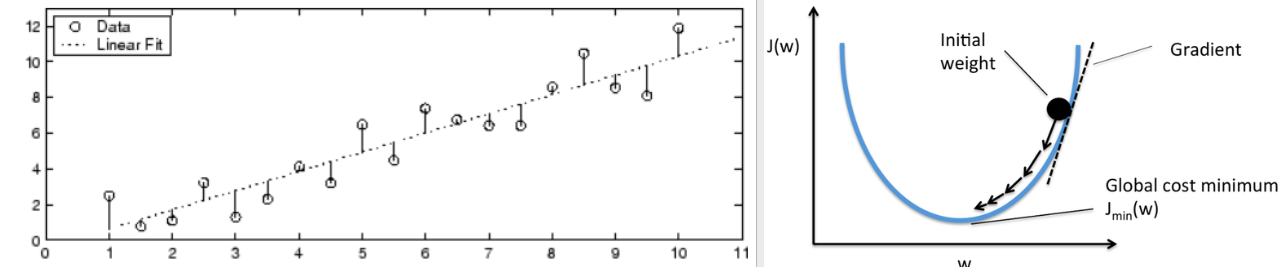
[우] : cost(손실)그래프. 기울기가 0이 되는 지점(w)이 최적의 추세선이다.

🧾선형회귀 분석 실습

방법1 : make_regression (model 생성 X)

from sklearn.datasets import make_regression
  • 각각의 데이터에 대한 잔차 제곱의 합이 최소가 되는 추세선을 만들고,
    이를 통해 독립변수 (x:연속형)가 종속변수(y:연속형)에 얼마나 영향을 주는지 인과관계를 분석
  • 회귀 분석 시험용 가상 데이터를 생성하는 명령어인 make_regression() 이 있다.
    옵션에 대한 자세한 정보는 이곳을 참고하자
from sklearn.datasets import make_regression
x,y,coef = make_regression(n_samples=50, n_features=1,bias=100,coef=True)
#회귀식(모델) => y = wx+b ::  y = 89.47.. * x + 100

선형회귀계수 (89.47..) 을 구해 회귀식모델을 만들었다. 이를 통해 미지수 값을 예측할 수 있다.
x값에 임의의 수를 넣어보자.

#미지수 값 예측
y_pred_new = 89.474 * 33 + 100
print(y_pred_new) #3052.64

방법2 : LinearRegression (model 생성 O)

from sklearn.linear_model import LinearRegression
  • 머신러닝은 귀납적 추론방식을 따른다.
  • 방법1에서 생성한 샘플을 사용했다.
  • LinearRegression으로 모델을 만들고 fit함수로 학습했다.
from sklearn.linear_model import LinearRegression
model = LinearRegression()
fit_model = model.fit(xx,yy) #학습데이터로 모델 추정. bias(절편),기울기 얻음

print('기울기',fit_model.coef_) #89.47
print('bias',fit_model.intercept_) #100.0 #방법1과 같음
  • predict : 얻어낸 계수로 예측을 할때 LinearRegression에서는 예측값 확인 함수를 지원한다.
#기존 학습데이터로 검정(2차원배열값)
y_new = fit_model.predict(xx[[0]]) 
print('y_new : ',y_new) #-52.172


#새로운 자료로 예측
y_new = fit_model.predict([[12]])
# result : 1173.691

방법3 : ols (model 생성 O)

import statsmodels.formula.api as smf

  • 최소자승법 : 잔차제곱합(RSS: Residual Sum of Squares)를 최소화하는 가중치 벡터를 구하는 방법

  • model변수는 smf의 ols(최소제곱법)을 사용하여 회귀모형을 만든다.
    Formula = '종속변수 ~ 독립변수' 형식에 맞춰 분석하고자 하는 종속변수(왼쪽)와 독립변수(오른쪽)를 넣으면된다.

  • data에는 사용하고자하는 데이터를 넣어주면 된다. fit은 모형을 적합시킨다

import statsmodels.formula.api as smf
import pandas as pd
x1 = xx.flatten() #2->1차원으로 축소
y1 = yy

data = np.array([x1,y1])
df = pd.DataFrame(data.T) #배열 전치

#formula 종속~독립변수
model2 = smf.ols(formula='y1 ~ x1',data=df).fit()
print(model2.summary()) #ols가 지원하는 보고서

예측하는 방법

#예측 (검정)
new_df = pd.DataFrame({'x1':[-1.70073563,-0.67794537]})
new_pred = model2.predict(new_df)
print(new_pred)
#새로운 값으로 예측
new2_df = pd.DataFrame({'x1':[-1.000,12]})
new2_pred = model2.predict(new2_df)
print(new2_pred)
  • 모델 생성 후 fit()으로 학습하고 predict()으로 예측결과를 얻었다.
  • 보고서를 작성할 땐 ols 라이브러리는 매우 중요하다.

📋예제

IQ와 시험성적 간의 인과관계 확인. 시험점수값 예측하기
score_iq = pd.read_csv("../testdata/score_iq.csv")

sid  score   iq  academy  game  tv
0  10001     90  140        2     1   0
1  10002     75  125        1     3   3
		....
  1. 상관계수 확인
score_iq = pd.read_csv("../testdata/score_iq.csv")
iq = score_iq.iq
score = score_iq.score


# 상관계수 확인
print(np.corrcoef(iq,score)) #양의상관관계 : 0.88
print(score_iq.corr())
  1. 인과관계 (선형회귀분석모델) linregress
model = stats.linregress(iq,score)
print('slope: ',model.slope) #기울기 0.651
print('intercept: ',model.intercept) #절편 -2.85
print('pvalue: ',model.pvalue) #pvalue 2.84e-50
print('stderr : ',model.stderr) #표준오차 0.0285

  • pvalue < 0.05 이므로 (iq/score)는 인과관계가 있다.

  • slope : iq는 시험성적에 0.651배 만큼 영향을 준다

Cost Minimization.
predict 함수를 지원하지 않아 수식을 직접 작성한다.

plt.scatter(iq,score)
plt.plot(iq,model.slope * iq + model.intercept)
plt.show()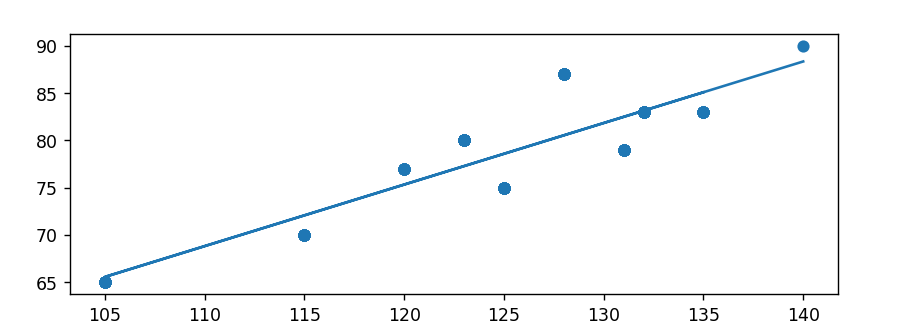


점수 예측

  • predict() 제공하지않음.
    대신 numpy의 polyval()을 사용할 수 있다.
#수식
preScore = model.slope * 112 + model.intercept
print(preScore)

#함수
# 새로운 iq값으로 성적 예측
new_df = pd.DataFrame({'iq':[55,66,77,88,99,111]})
print('점수예측값',np.polyval([model.slope,model.intercept],\
                        new_df))
점수예측값 [32.97] [40.13] [47.30] [54.46] [61.63] [69.45]
profile
kangjuju
이전 포스트

상관관계

다음 포스트

OLS Regression Results

0개의 댓글