Basic ML_2

1. Multinomial Classification - Softmax Regression

Softmax Regression : 이진 분류가 아닌 다중 분류를 해결하기 위한 모델

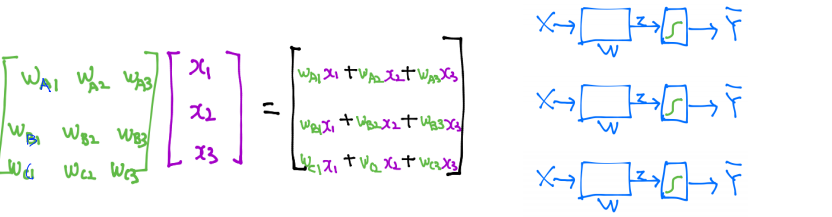
• Softmax Classifier의 cost함수
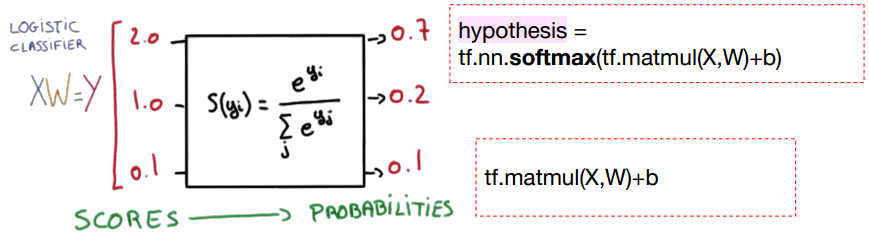  p는 확률로 0.7 + 0.2 + 0.1 = 1이 된다.
  즉, 여러개의 연산결과를 정규화하여 모든 클래스의 확률값의 합을 1로 만든다. (softmax는 확률 값으로 만든다.)
  확률을 구한다음 one-hot encoding을 사용하여 max값을 1로 만들고 나머지는 모두 0으로 만든다.
  즉 정답 클래스를 one-hot encoding 방식으로 학습시킨다.

• CROSS-ENTROPY cost function
  

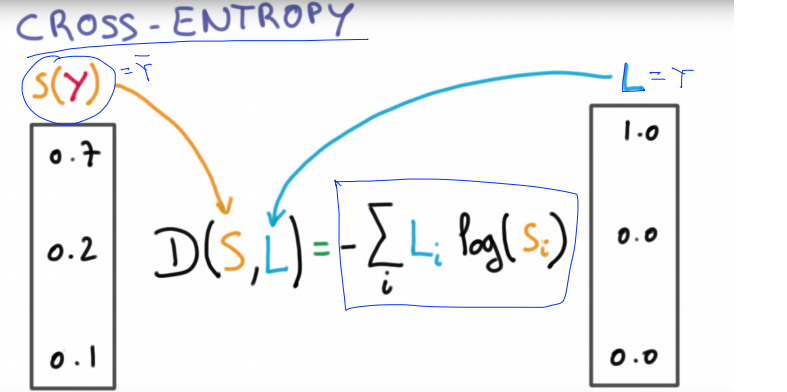
2. Softmax classifier Tensorflow

import tensorflow as tf
import numpy as np

x_data = [[1, 2, 1, 1],
          [2, 1, 3, 2],
          [3, 1, 3, 4],
          [4, 1, 5, 5],
          [1, 7, 5, 5],
          [1, 2, 5, 6],
          [1, 6, 6, 6],
          [1, 7, 7, 7]]
y_data = [[0, 0, 1],
          [0, 0, 1],
          [0, 0, 1],
          [0, 1, 0],
          [0, 1, 0],
          [0, 1, 0],
          [1, 0, 0],
          [1, 0, 0]]

#convert into numpy and float format
# np.asarra() : 다차원배열을 ndarray 만들기
x_data = np.asarray(x_data, dtype=np.float32)
y_data = np.asarray(y_data, dtype=np.float32)

#dataset을 선언합니다.
dataset = tf.data.Dataset.from_tensor_slices((x_data, y_data))
dataset = dataset.repeat().batch(2)

nb_classes = 3 #class의 개수입니다.

print(x_data.shape)
print(y_data.shape)

(8, 4)
(8, 3)

#Weight and bias setting
W = tf.Variable(tf.random.normal((4, nb_classes)), name='weight')
b = tf.Variable(tf.random.normal((nb_classes,)), name='bias')
variables = [W, b]

# tf.nn.softmax computes softmax activations
# softmax = exp(logits) / reduce_sum(exp(logits), dim)
def hypothesis(X):
    return tf.nn.softmax(tf.matmul(X, W) + b) # matmul() : matrix 곱

# Softmax onehot test
sample_db = [[8,2,1,4]]
sample_db = np.asarray(sample_db, dtype=np.float32)

def cost_fn(X, Y):
    logits = hypothesis(X)
    cost = -tf.reduce_sum(Y * tf.math.log(logits), axis=1)
    cost_mean = tf.reduce_mean(cost)
    
    return cost_mean

x = tf.constant(3.0)
with tf.GradientTape() as g:
    g.watch(x)
    y = x * x # x^2
dy_dx = g.gradient(y, x) # Will compute to 6.0

def grad_fn(X, Y):
    with tf.GradientTape() as tape:
        loss = cost_fn(X, Y)
        grads = tape.gradient(loss, variables)

        return grads

print(grad_fn(x_data, y_data))


def fit(X, Y, epochs=2000, verbose=100):
    optimizer =  tf.keras.optimizers.SGD(learning_rate=0.1)

    for i in range(epochs):
        grads = grad_fn(X, Y)
        optimizer.apply_gradients(zip(grads, variables))
        if (i==0) | ((i+1)%verbose==0):
            print('Loss at epoch %d: %f' %(i+1, cost_fn(X, Y).numpy()))
            
fit(x_data, y_data)

Loss at epoch 1: 9.806579
Loss at epoch 100: 0.690391
Loss at epoch 200: 0.580549
Loss at epoch 300: 0.521439
Loss at epoch 400: 0.475617
Loss at epoch 500: 0.435717
Loss at epoch 600: 0.398926
Loss at epoch 700: 0.363617
Loss at epoch 800: 0.328556
Loss at epoch 900: 0.292792
Loss at epoch 1000: 0.256996
Loss at epoch 1100: 0.233967
Loss at epoch 1200: 0.222449
Loss at epoch 1300: 0.212050
Loss at epoch 1400: 0.202543
Loss at epoch 1500: 0.193821
Loss at epoch 1600: 0.185789
Loss at epoch 1700: 0.178372
Loss at epoch 1800: 0.171503
Loss at epoch 1900: 0.165123
Loss at epoch 2000: 0.159185

prediction check

sample_data = [[2,1,3,2]] # answer_label [[0,0,1]]
sample_data = np.asarray(sample_data, dtype=np.float32)

a = hypothesis(sample_data)
b = hypothesis(x_data)
print(b)
print(tf.argmax(b, 1))
print(tf.argmax(y_data, 1)) # matches with y_data

class softmax_classifer(tf.keras.Model):
    def __init__(self, nb_classes):
        super(softmax_classifer, self).__init__()
        self.W = tf.Variable(tf.random.normal((4, nb_classes)), name='weight')
        self.b = tf.Variable(tf.random.normal((nb_classes,)), name='bias')
        
    def softmax_regression(self, X):
        return tf.nn.softmax(tf.matmul(X, self.W) + self.b)
    
    def cost_fn(self, X, Y):
        logits = self.softmax_regression(X)
        cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.math.log(logits), axis=1))        
        return cost
    
    def grad_fn(self, X, Y):
        with tf.GradientTape() as tape:
            cost = self.cost_fn(x_data, y_data)
            grads = tape.gradient(cost, self.variables)            
            return grads
    
    def fit(self, X, Y, epochs=2000, verbose=500):
        optimizer =  tf.keras.optimizers.SGD(learning_rate=0.1)

        for i in range(epochs):
            grads = self.grad_fn(X, Y)
            optimizer.apply_gradients(zip(grads, self.variables))
            if (i==0) | ((i+1)%verbose==0):
                print('Loss at epoch %d: %f' %(i+1, self.cost_fn(X, Y).numpy()))
            
model = softmax_classifer(nb_classes)
model.fit(x_data, y_data)

Loss at epoch 1: 2.472669
Loss at epoch 500: 0.375229
Loss at epoch 1000: 0.229923
Loss at epoch 1500: 0.182147
Loss at epoch 2000: 0.150633

3. Fancy Softmax classifier Tensorflow

logits = tf.matmul(X,W) + b
hypothesis = tf.nn.softmax(logits)

# Cross entropy cost/loss
cost_i = tf.nn.softmax_cross_entropy_with_logits_v2(logits=logits,
 labels=Y_one_hot)
cost = tf.reduce_mean(cost_i)

1) Load Dataset

import tensorflow as tf
import numpy as np
import os
from google.colab import drive

tf.random.set_seed(777)  # for reproducibility

xy = np.loadtxt('/content/gdrive/My Drive/data-04-zoo.csv', delimiter=',', dtype=np.float32)
x_data = xy[:, 0:-1]
y_data = xy[:, -1]

nb_classes = 7 # 0 ~ 6

# Make Y data as onehot shape
Y_one_hot = tf.one_hot(y_data.astype(np.int32), nb_classes)
print(x_data.shape, Y_one_hot.shape)

결과 : (101, 16) (101, 7)

2) Softmax Classifier

#Weight and bias setting
W = tf.Variable(tf.random.normal((16, nb_classes)), name='weight')
b = tf.Variable(tf.random.normal((nb_classes,)), name='bias')
#업데이트할 variables는 따로 저장
variables = [W, b]

def logit_fn(X):
  return tf.matmul(X,W) + b

#softmax = exp(logits)
def hypothesis(X):
  return tf.nn.softmax(logit_fn(X))

def cost_fn(X, Y):
  logits = logit_fn(X)
  cost_i = tf.keras.losses.categorical_crossentropy(y_true=Y, y_pred=logits, from_logits=True)
  cost = tf.reduce_mean(cost_i)
  return cost

def grad_fn(X,Y):
  with tf.GradientTape() as tape:
    loss = cost_fn(X,Y)
    grads = tape.gradient(loss, variables)
    return grads

def prediction(X,Y):
  pred = tf.argmax(hypothesis(X),1)
  correct_prediction = tf.equal(pred, tf.argmax(Y,1))
  accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
  return accuracy

3) 학습하기

def fit(X,Y, epochs=1000, verbose=100):
  #optimizer : learning_rate의 값에 따라 variables 수정
  optimizer =  tf.keras.optimizers.SGD(learning_rate=0.1)
  
  for i in range(epochs):
    grads = grad_fn(X, Y)
    optimizer.apply_gradients(zip(grads, variables))
    if (i==0) | ((i+1)%verbose==0):
      acc = prediction(X, Y).numpy()
      loss = cost_fn(X, Y).numpy() 
      print('Steps: {} Loss: {}, Acc: {}'.format(i+1, loss, acc))

fit(x_data, Y_one_hot)

4. Learning Rate(학습률)과 데이터 전처리

• Learning Rate
  Learning rate와 Gradient를 통해서 기울기를 작게 만들어 cost의 최적값을 찾을 수 있다.
  annealing the learning rate : learning rate을 적절히 조절. (= learning rate decay)

  tf.train.exponential_decay(starter_learning_rate, global_step, 1000, 0.96, staircase=True)
  #(시작값, 전체 스텝, 1000번째 스텝마다, 0.96 만큼, learning rate 값을 조절할 것이다.)

• Data preprocessing 데이터 전처리
  1) feature scaling
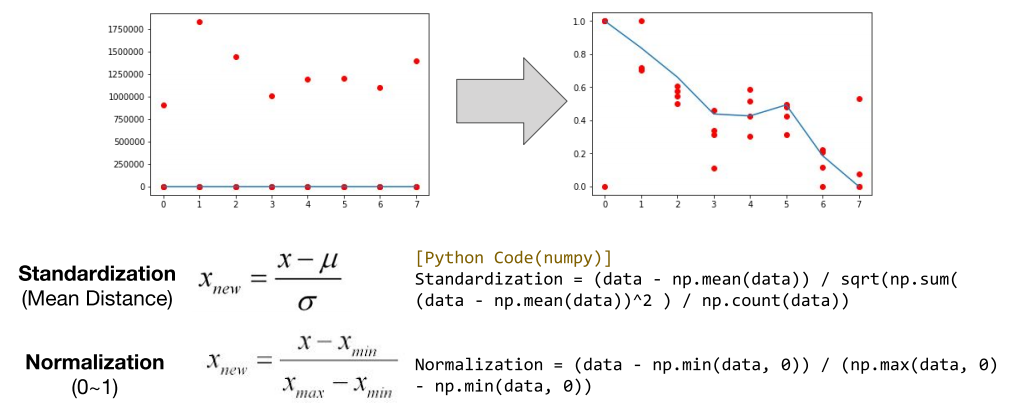  Standardization 표준화 기법 : (x - 평균)/표준편차 → 평균에서 얼마만큼 떨어져 있는지를 표현.
  Normalization 정규화 기법 : 불필요한 데이터를 0 ~ 1사이의 동일 표면에 골고루 표현한다.
  2) Noisy data 없애기
  불필요한 데이터인 noisy data를 제외하고 깔끔한 데이터로만 표현한다.

5. Overfitting Solutions

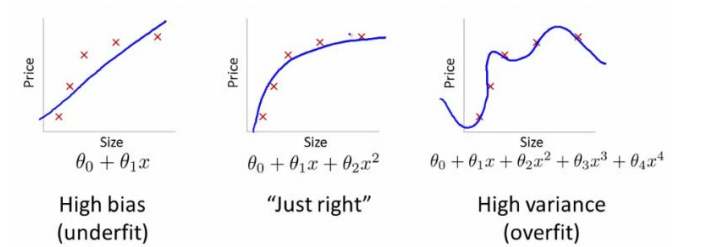overfitting : 과하게 맞추어져있다.

• set a feature에 따라 overfitting을 해결할 수 있다.
  학습을 위한 데이터를 더 많이 넣는다.
  feature 수를 줄인다. (차원을 줄임으로서 모델을 더 잘 찾을 수 있다)
    👉 sklearn code를 사용해서 자원을 줄일 수 있다.
  underfitting 상태일 땐 feature의 수를 늘린다.
• Regularization
  학습을 통해 특정값을 추가해 정규화
  하나의 숫자가 너무 차이가 나서 조금 더 평평한 구간으로 만들어 정규화시키기 위해 람다값을 추가
  

6. Learning rate, 전처리, overfitting Tensorflow

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import tensorflow as tf
tf.random.set_seed(777)  # for reproducibility

xy = np.array([[828.659973, 833.450012, 908100, 828.349976, 831.659973],
               [823.02002, 828.070007, 1828100, 821.655029, 828.070007],
               [819.929993, 824.400024, 1438100, 818.97998, 824.159973],
               [816, 820.958984, 1008100, 815.48999, 819.23999],
               [819.359985, 823, 1188100, 818.469971, 818.97998],
               [819, 823, 1198100, 816, 820.450012],
               [811.700012, 815.25, 1098100, 809.780029, 813.669983],
               [809.51001, 816.659973, 1398100, 804.539978, 809.559998]])

x_train = xy[:, 0:-1]
y_train = xy[:, [-1]]

plt.plot(x_train, 'ro')
plt.plot(y_train)
plt.show()

# 특정 값이 차이가 많이 날 때 사용
def normalization(data):
  numerator = data - np.min(data, 0)
  denominator = np.max(data,0) - np.min(data, 0)
  return numerator/denominator

xy = normalization(xy)
print(xy)
x_train = xy[:, 0:-1]
y_train = xy[:, [-1]]

plt.plot(x_train, 'ro')
plt.plot(y_train)

plt.show()

dataset = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(len(x_train))

W = tf.Variable(tf.random.normal((4,1)),dtype = tf.float32)
b = tf.Variable(tf.random.normal((1,)), dtype = tf.float32)

# Linear Regression hypothesis 정의 (y= Wx+b)
def linearReg_fn(features):
  hypothesis = tf.matmul(features,W) + b
  return hypothesis

# 특정값이 있을 때 하나의 특정값이 영향을 크게 줄 때 weight을 정규화
def l2_loss(loss, beta = 0.01):
  W_reg = tf.nn.l2_loss(W)
  loss = tf.reduce_mean(loss + W_reg * beta)
  return loss

# cost를 구하고 l2_loss를 적용할것인지 정해준다.
def loss_fn(hypothesis, features, labels, flag=False):
  cost = tf.reduce_mean(tf.square(hypothesis - labels))
  if(flag):
    cost = l2_loss(cost)
  return cost
  
  is_decay = True
starter_learning_rate = 0.1

if(is_decay):
  learning_rate = tf.keras.optimizers.schedules.ExponentialDecay(initial_learning_rate=starter_learning_rate, decay_steps=50,
                   decay_rate=0.96, staircase=True)
  optimizer = tf.keras.optimizers.SGD(learning_rate)
else : 
  optimizer = tf.keras.optimizers.SGD(learning_rate=starter_learning_rate)

def grad(hypothesis, features, labels, l2_flag):
    with tf.GradientTape() as tape:
        loss_value = loss_fn(linearReg_fn(features),features,labels, l2_flag)
    return tape.gradient(loss_value, [W,b]), loss_value
    
    EPOCHS = 101

for step in range(EPOCHS):
    for features, labels  in dataset:
        features = tf.cast(features, tf.float32)
        labels = tf.cast(labels, tf.float32)
        grads, loss_value = grad(linearReg_fn(features), features, labels, False)
        optimizer.apply_gradients(grads_and_vars=zip(grads,[W,b]))        
    if step % 10 == 0:
        print("Iter: {}, Loss: {:.4f}".format(step, loss_value))