DP의 대표격인 0-1 Knapsack 문제를 정리해보자.
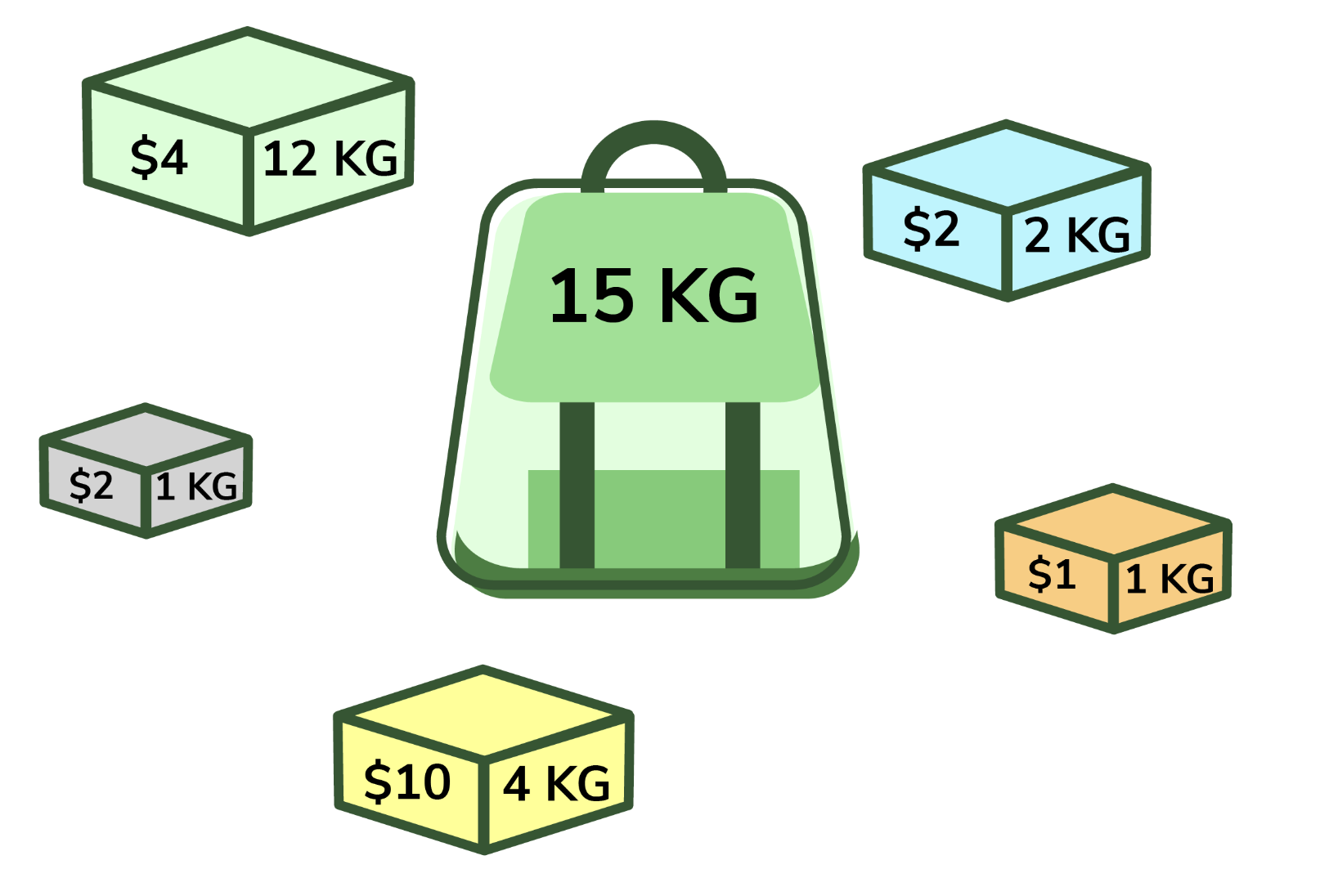
조건
- 아이템을 선택하거나 선택하지 않거나 둘 중 하나만 가능. (0-1)
- 각 아이템은 무게(Weight)와 가치(Value)를 지닌다.
기본 Knapsack
최대 W의 무게에서, 최대 가치의 조합을 찾아라.
기본 Knapsack 문제는 일차원 배열 혹은 이차원 배열로 해결할 수 있다.
일차원 DP
- dp[w] = 무게 w일 때의 최대 가치
이차원 DP
- dp[i][w] = i번째 아이템까지 고려했을 때, 총 무게가 w일 때의 최대 가치
두 해결 방법 모두 시간복잡도는 O(NW)로 동일하지만,
공간복잡도는 O(W), O(NW)로 다르다.
따라서 아이템의 개수(N)가 많고, 선택한 아이템을 역추적할 필요가 없으면,
일차원 DP로 해결하는 것이 적절하다.
일차원 DP 알고리즘
int[] dp = new int[maxWeight];
//모든 아이템에 대해
for(int i = 0; i < N; i++) {
int tmpWeight = //현재 아이템 무게
int tmpValue = //현재 아이템 가치
// *중요 뒤에서부터 순회 (중복 선택 방지)
for(int w = maxWeight; w >= tmpWeight; w--) {
dp[w] = Math.max(dp[w], dp[w - tmpWeight] + tmpValue);
}
}
점화식
dp[w] = Math.max(dp[w], dp[w - tmpWeight] + tmpValue)
현재 무게(w) 에서의 최대 가치를,
현재 아이템을 넣는 것을 고려했을 때의 가치와 비교하여 갱신한다.
앞에서부터 순회할 경우 현재 아이템을 중복으로 삽입하는 것이므로 주의.
이차원 DP 알고리즘
int[] dp = new int[N][maxWeight]
//모든 아이템에 대해
for(int i = 0; i < N; i++) {
int tmpWeight = //현재 아이템 무게
int tmpValue = //현재 아이템 가치
for(int w = 0; w < maxWeight; w++) {
if(w < tmpWeight) {
dp[i][w] = dp[i-1][w]; //현재 아이템을 못넣음
} else {
dp[i][w] = Math.max(
dp[i-1][w], //아이템을 안넣음
dp[i-1][w - tmpWeight] + tmpValue //아이템을 넣음
)
}
}
}
점화식
현재 무게(w) 보다 아이템의 무게가 큰 경우 (아이템을 넣지 못할때)
dp[i][w] = dp[i-1][w]
현재 무게(w) 가 아이템의 무게보다 크거나 같은 경우 (아이템을 넣을 수 있을 때)
dp[i][w] = Math.max(dp[i-1][w], dp[i-1][w-tmpWeight] + tmpValue
일차원 DP와 마찬가지로 현재 무게에서의 최대 가치를,
현재 아이템을 넣는 것을 고려했을 때의 가치와 비교하여 갱신하면 된다.
선택 역추적
이차원 배열을 갱신할 때,
아이템을 선택한 경우 dp[i][w] = dp[i-1][w-tmpWeight] + tmpValue로 갱신된다.
즉, dp[i][w] == dp[i-1][w] 인 경우 i 번째 아이템은 선택하지 않은 것이다.
dp[N][W] 에서 시작하여,
if(dp[i][w] == dp[i-1][w])-> i 번째 아이템은 선택 X,i--else-> i 번째 아이템 선택 O,i--,w = w - weight[i]
변형 Knapsack
V의 가치 이상을 만족하는 조합 중, 최소 무게를 찾아라.
변형이라고는 하지만 위의 두 방식으로도 해결이 가능하다.
- 1차원 배열을 처음부터 순회하며, 값이 V 이상인 최소 무게를 찾는다.
- 2차원 배열의 마지막 row를 순회하며 값이 V 이상인 최소 무게를 찾는다.
하지만, 기본 Knapsack은 가방의 크기(최대 무게)를 문제에서 제약조건으로 제시하므로, 크기가 합리적인 수준인 경우가 대부분이다.
변형 Knapsack 같은 경우 각 아이템의 크기의 합이 엄청나게 커질 수 있으므로, 최대 무게(모든 아이템 무게의 합)에 맞춰 배열을 만들수 없는 경우가 발생한다.
그럴 때는 가치(V) 기준으로 배열을 만들어서 해결할 수 있다.
일차원 DP
- dp[v] = 가치 V일 때의 최소 무게
//maxValue = sum of all item value
int[] dp = new int[maxValue + 1]
Arrays.fill(dp, INF);
dp[0] = 0;
//모든 아이템에 대해
for(int i = 0; i < N; i++) {
int tmpWeight = //현재 아이템 무게
int tmpValue = //현재 아이템 가치
// *중요 뒤에서부터 순회 (중복 선택 방지)
for(int v = maxValue; v >= tmpValue; v--) {
dp[v] = Math.min(dp[v], dp[v - tmpValue] + tmpWeight);
}
}
int answer = 0;
for(int v = targetValue; v <= maxValue; v++) {
answer = Math.min(answer, dp[v]);
}시간복잡도는 O(NW)로 동일하지만, 공간복잡도가 O(W)가 아닌, O(V)로 변경되었다.
주어진 문제에서 무게에 비해 가치의 합이 크지 않을 경우 위 방법을 사용하면 된다.

