CNN
-
CNN은 Convolution Neural Network의 약자로 이미지 처리에 특화된 네트워크이다.
CNN의 과정과 사람의 인지과정을 간단히 살펴보면 아래와 같다.
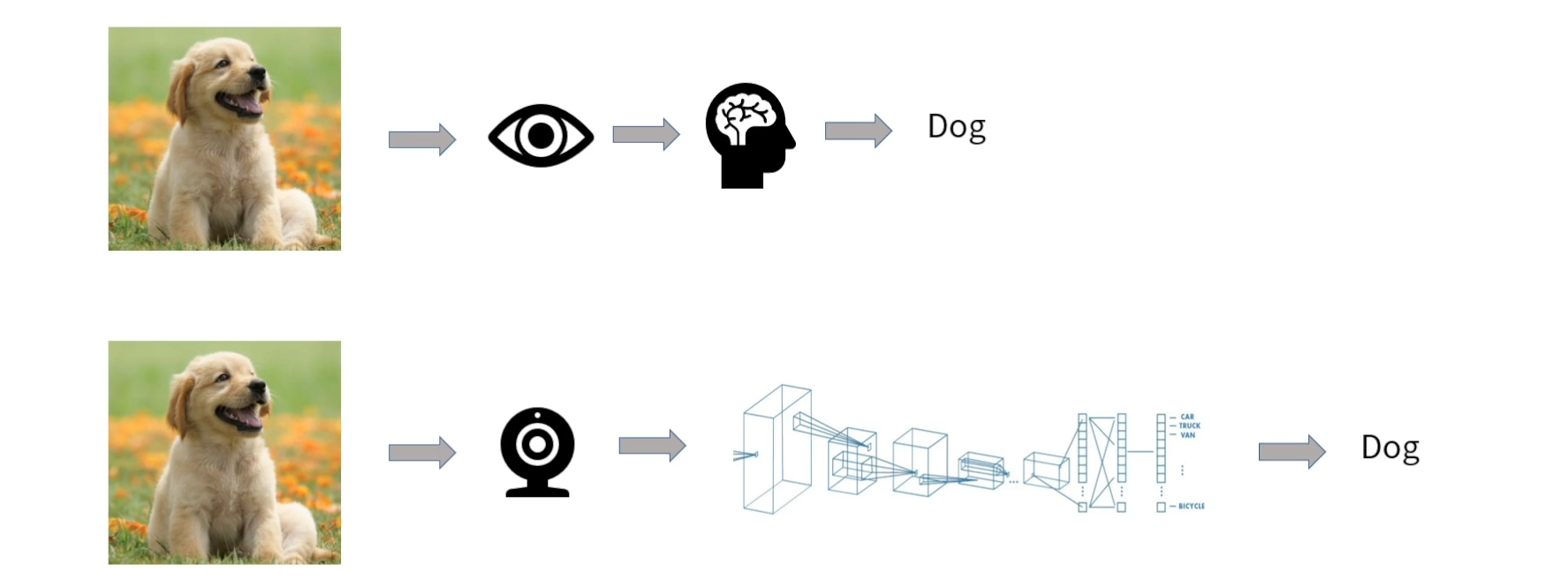
컨볼루션 매트릭스라고 하여 (3x3, 5x5)의 작은 커널을 가진 연산을 하는 작업을 컨볼루션이라고 한다.
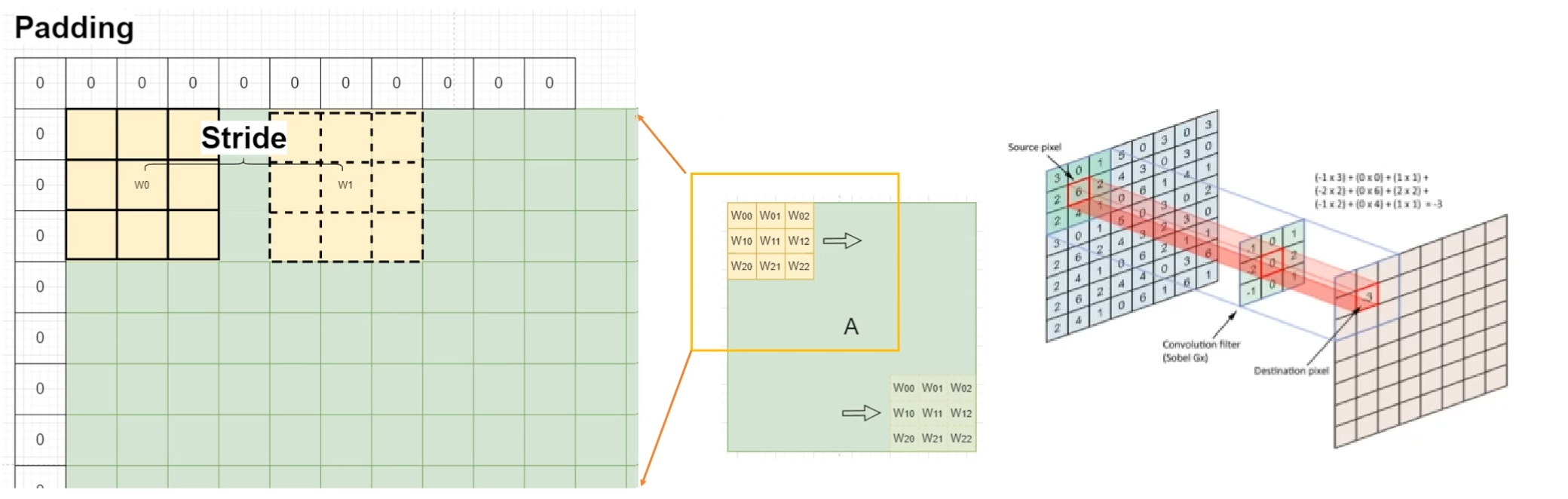
Padding : Add zero values in boundary of input image
Stride : Elements of sliding window of convolution kernelOutput shape
- oh = (ih - kh + padding*2)//stride + 1
- ow = (iw - kw + padding*2)//stride + 1
- b : batch
- ic : in_channel
- ih : in_height
- iw : in_width
- oc : out_channel
- kh : kernel_h
- kw : kernel_w
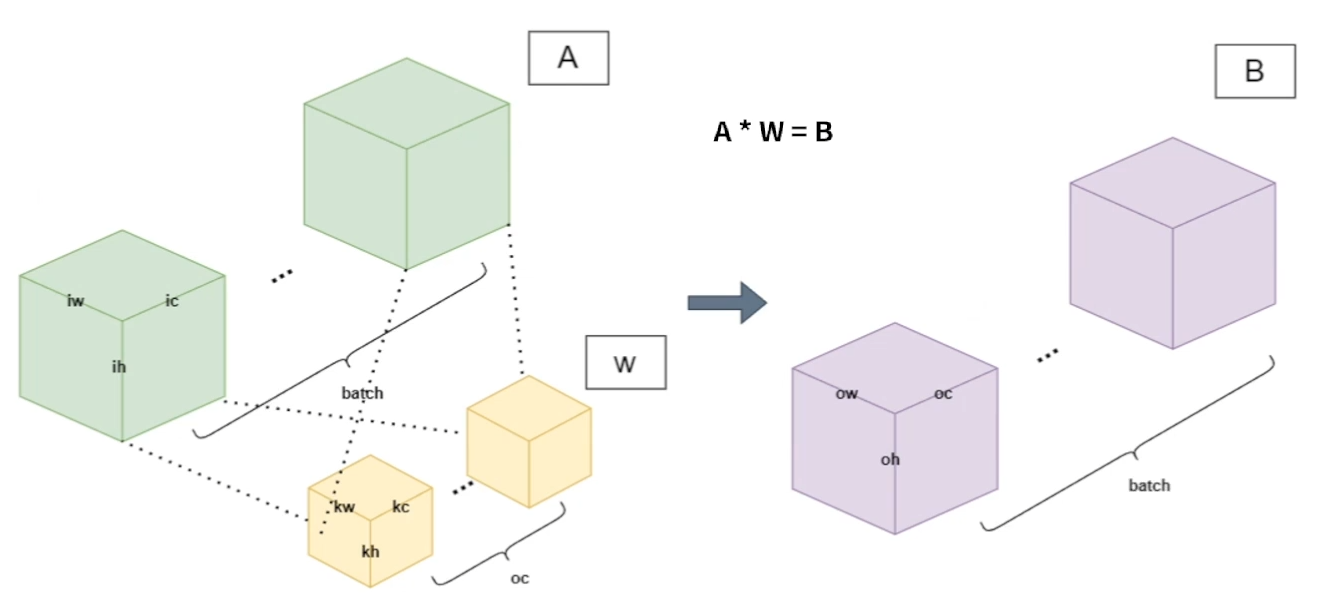
- A shape : [b, ic, ih, iw]
- W shape : [oc, kc, kh, kw]
- B shape : [b, oc, oh, ow]
- Weight sharing between batch of A
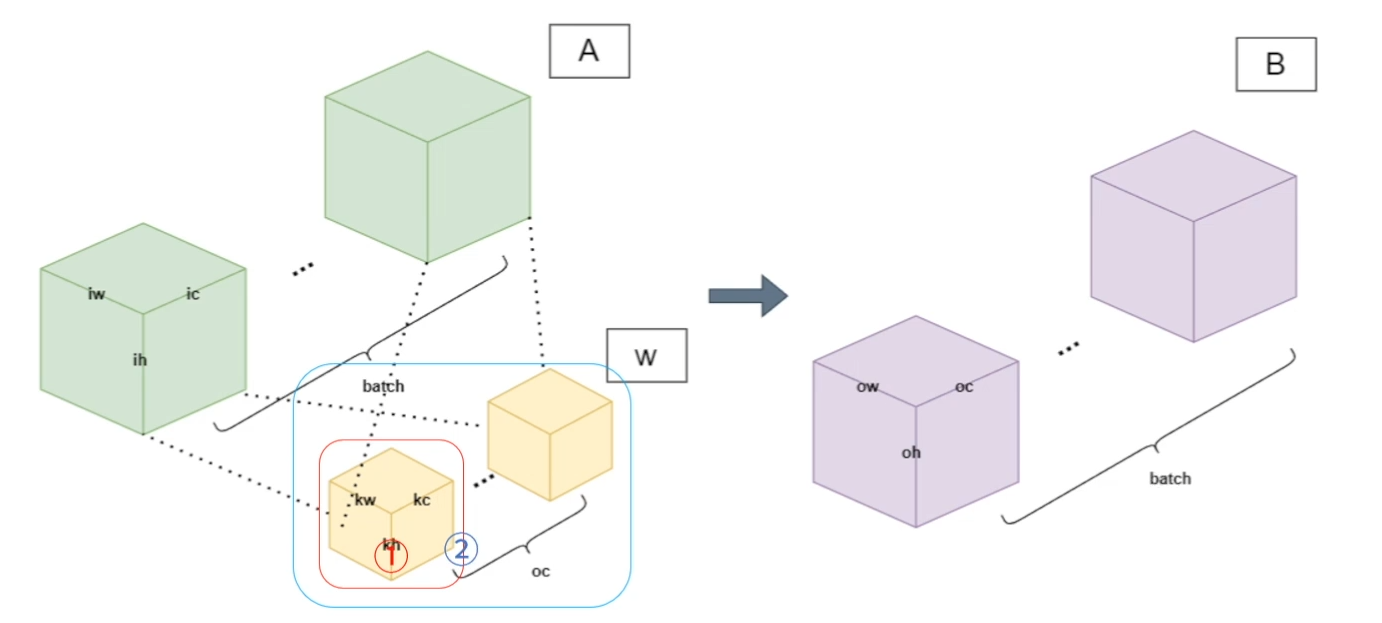
- Convolution Operation
- MAC(Multiply Accumulation operation)
- Convolution MAC : kw x kh x kc x oc x ow x oh x b
① : kw x kh x oc, ② : kw x kh x kc x oc
- Convolution MAC : kw x kh x kc x oc x ow x oh x b
# 7 loops in convolution operation
for b in batch:
for oh in out_height:
for ow in out_width:
for oc in out_channel:
for kc in kernel_channel:
for kh in kernel_height:
for kw in kernel_width: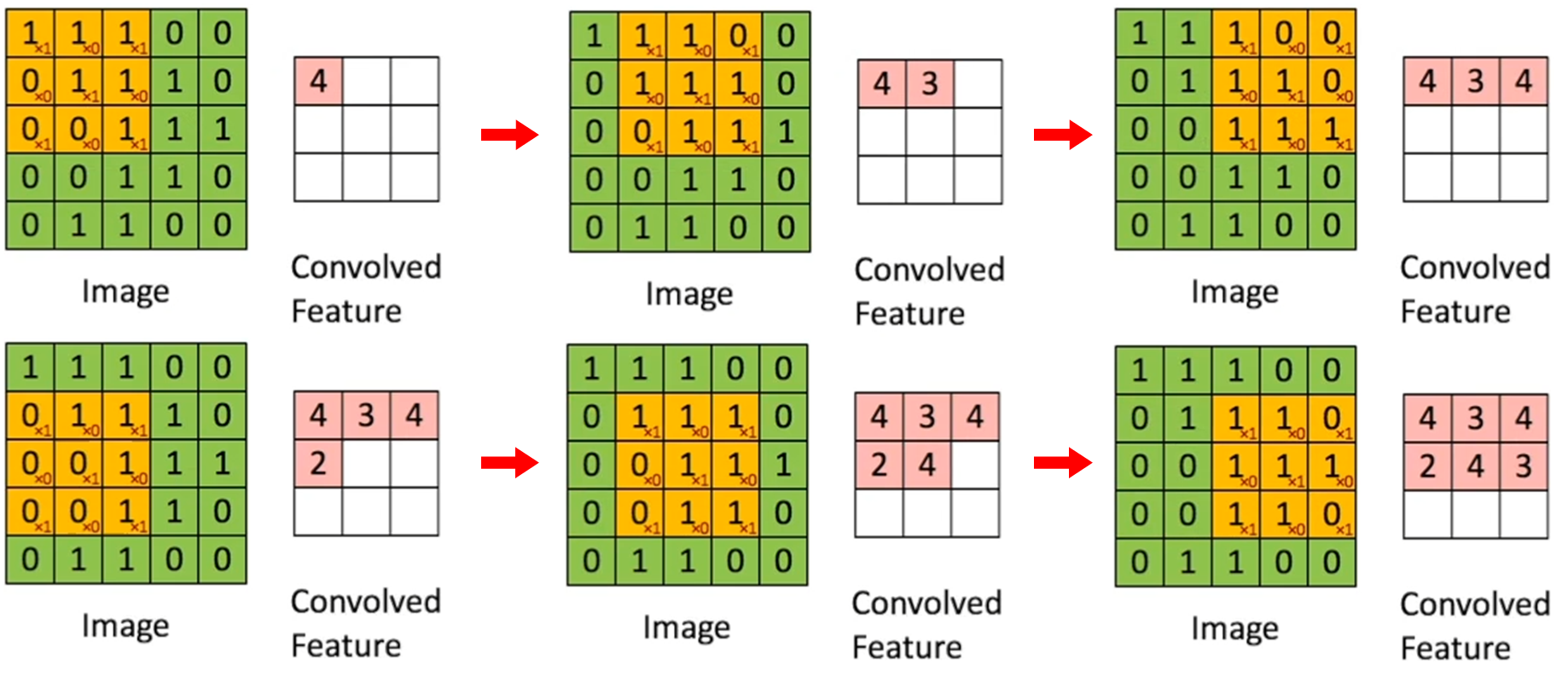
- IM2COL & GEMM
- IM2COL
- Transform n-dimension data into 2D matrix data
- more efficient operation!!
- GEMM
- General Matrix to Matrix Multiplication
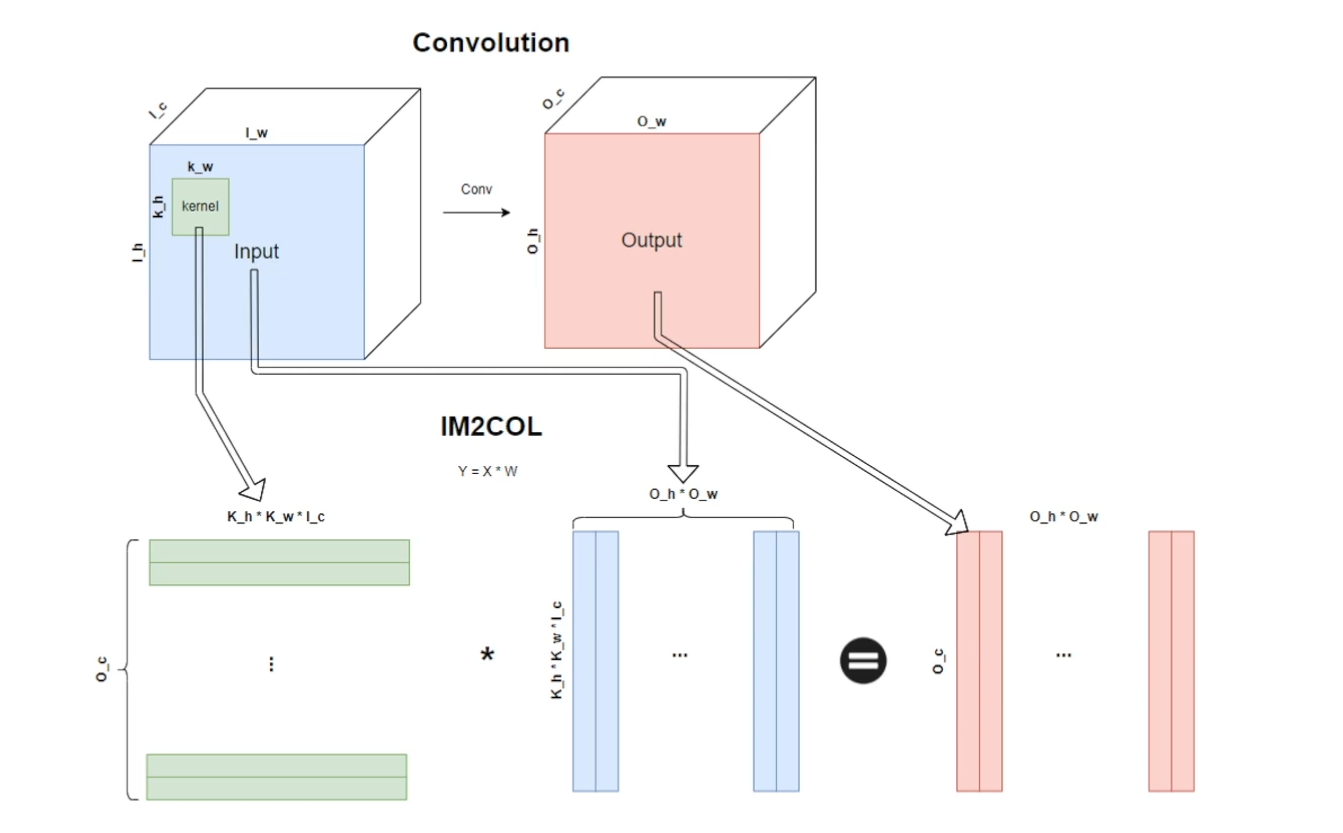
- IM2COL
Sliding window Convolution
- 시간 측정 결과 -> L1 time : 0.0365447998046875
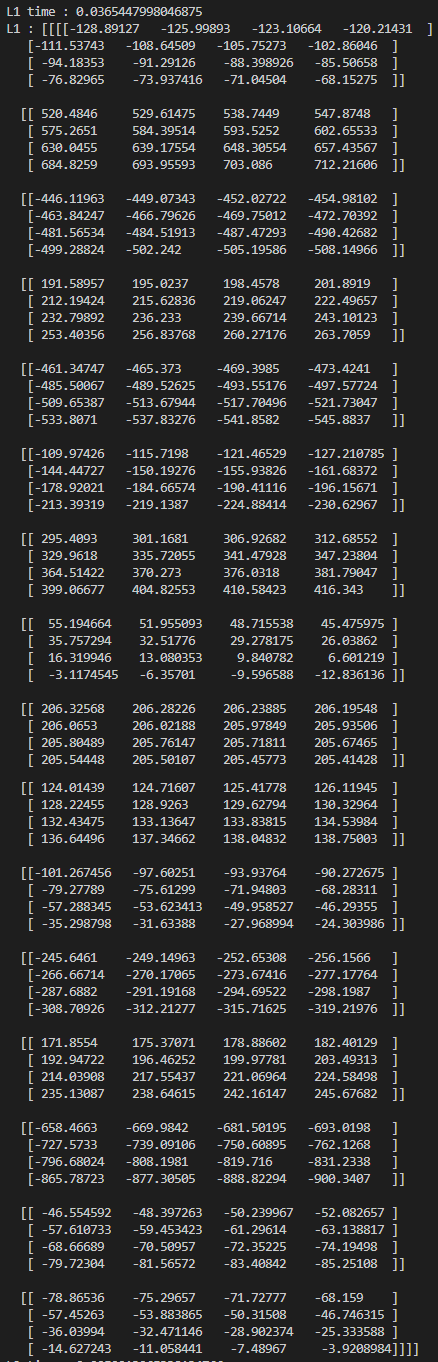
IM2COL GEMM convolution
- 시간 측정 결과 -> L2 time : 0.0050013065338134766
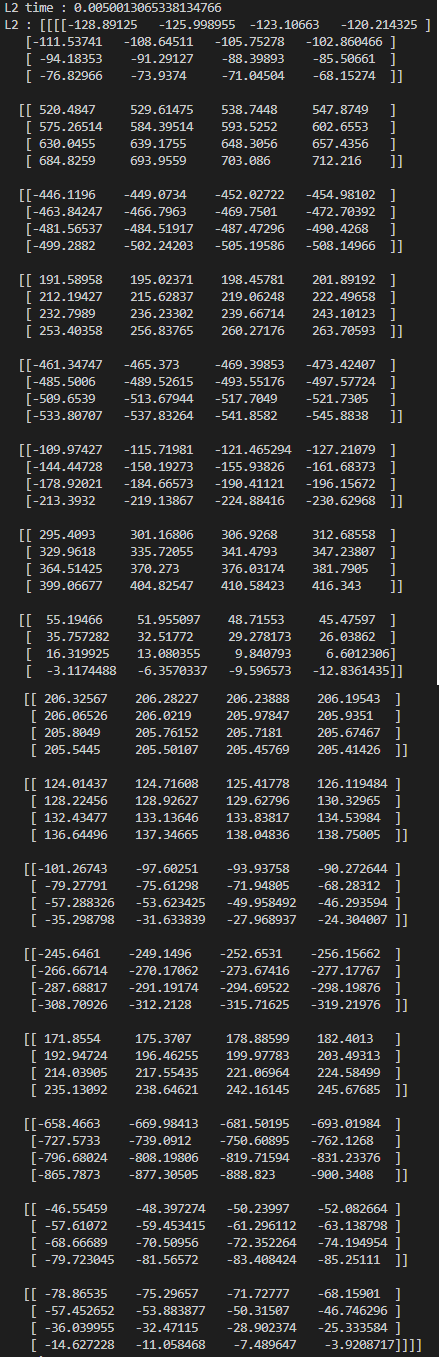
pytorch convolution
- 시간 측정 결과 -> L3 time : 0.0
| Sliding window | IM2COL GEMM | pytorch | |
|---|---|---|---|
| 시간 | 0.0365447998046875 | 0.0050013065338134766 | 0 |
측정된 시간은 위와 같으며 각각의 tensor의 내용을 살펴보면 3가지 convolution 모두 동일한 것을 확인할 수 있다.
코드
main
import numpy as np
import time
import torch
import torch.nn as nn
from function.convolution import Conv
def convolution():
print("convolution")
# define the shape of input & weight
in_w = 6
in_h = 6
in_c = 3
out_c = 16
batch = 1
k_w = 3
k_h = 3
X = np.arange(in_w * in_h * in_c * batch, dtype=np.float32).reshape([batch, in_c, in_h, in_w])
W = np.array(np.random.standard_normal([out_c, in_c, k_h, k_w]), dtype=np.float32)
Convolution = Conv(batch=batch,
in_c=in_c,
out_c=out_c,
in_h=in_h,
in_w=in_w,
k_h=k_h,
k_w=k_w,
dilation=1,
stride=1,
pad=0)
# print(f"X = {X}")
# print(f"W = {W}, W.shape = {W.shape}")
L1_time = time.time()
for i in range(5):
L1 = Convolution.conv(X, W)
print(f"L1 time : {time.time() - L1_time}")
print(f"L1 : {L1}")
L2_time = time.time()
for i in range(5):
L2 = Convolution.gemm(X, W)
print(f"L2 time : {time.time() - L2_time}")
print(f"L2 : {L2}")
torch_conv = nn.Conv2d(in_c,
out_c,
kernel_size=k_h,
stride=1,
padding=0,
bias=False,
dtype=torch.float32)
torch_conv.weight = torch.nn.Parameter(torch.tensor(W))
L3_time = time.time()
for i in range(5):
L3 = torch_conv(torch.tensor(X, requires_grad=False, dtype=torch.float32))
print(f"L3 time : {time.time() - L3_time}")
print(f"L3 : {L3}")
if __name__ == "__main__":
convolution()convolution.py
import numpy as np
class Conv:
def __init__(self, batch, in_c, out_c, in_h, in_w, k_h, k_w, dilation, stride, pad):
self.batch = batch
self.in_c = in_c
self.out_c = out_c
self.in_h = in_h
self.in_w = in_w
self.k_h = k_h
self.k_w = k_w
self.dilation = dilation
self.stride = stride
self.pad = pad
self.out_h = (in_h - k_h + 2 * pad) // stride + 1
self.out_w = (in_w - k_w + 2 * pad) // stride + 1
def check_range(self, a, b):
return a > -1 and a < b
# naive convolution Sliding window metric
def conv(self, A, B):
C = np.zeros((self.batch, self.out_c, self.out_h, self.out_w), dtype=np.float32)
# seven loop
for b in range(self.batch):
for oc in range(self.out_c):
# each channel of output
for oh in range(self.out_h):
for ow in range(self.out_w):
# one pixel of output shape
a_j = oh * self.stride - self.pad
for kh in range(self.k_h):
if self.check_range(a_j, self.in_h) == False:
C[b, oc, oh, ow] += 0
else:
a_i = ow * self.stride - self.pad
for kw in range(self.k_w):
if self.check_range(a_i, self.in_w) == False:
C[b, oc, oh, ow] += 0
else:
C[b, oc, oh, ow] += np.dot(A[b, :, a_j, a_i], B[oc, :, kh, kw])
a_i += self.stride
a_j += self.stride
return C
# IM2COL. Change n-dim input to 2-dim matrix
def im2col(self, A):
# output
mat = np.zeros((self.in_c * self.k_h * self.k_w, self.out_w * self.out_h), dtype=np.float32)
mat_j = 0
mat_i = 0
for c in range(self.in_c):
for kh in range(self.k_h):
for kw in range(self.k_w):
in_j = kh * self.dilation - self.pad
for oh in range(self.out_h):
if not self.check_range(in_j, self.in_h):
for ow in range(self.out_w):
mat[mat_j, mat_i] = 0
mat_i += 1
else:
in_i = kw * self.dilation - self.pad
for ow in range(self.out_w):
if not self.check_range(in_i, self.in_w):
mat[mat_j, mat_i] = 0
mat_i += 1
else:
mat[mat_j, mat_i] = A[0, c, in_j, in_i]
mat_i += 1
in_i += self.stride
in_j += self.stride
mat_i = 0
mat_j += 1
return mat
# gemm. 2D matrix multiplication
def gemm(self, A, B):
a_mat = self.im2col(A)
b_mat = B.reshape(B.shape[0],-1)
c_mat = np.matmul(b_mat, a_mat)
c = c_mat.reshape([self.batch, self.out_c, self.out_h, self.out_w])
return chttps://github.com/Jun-yong-lee/pytorch_study/tree/Convolution
