
Deep Learning: 신경망의 기초 - 기계학습 II
1.3 데이터에 대한 이해
-
과학 기술의 발전 과정

- 예) 튀코 브라헤는 천동설이라는 틀린 모델을 선택함으로써 자신이 수집한 데이터를 설명하지 못함. 케플러는 지동설 모델을 도입하여 제1, 제2, 제 3법칙을 완성함
-
기계학습
- 기계 학습이 푸는 문제는 훨씬 복잡함
예) [그림 1-2]의 ‘8’ 숫자 패턴과 ‘단추’ 패턴의 다양한 변화 양상 - 단순한 수학 공식으로 표현 불가능함
- 데이터를 설명할 수 있는 학습 모델을 찾아내는 과정, 즉 기계학습에는 자동으로 모델을 찾아내는 과정이 필수

- 기계 학습이 푸는 문제는 훨씬 복잡함
1.3.1 데이터 생성 과정
- 데이터 생성 과정을 완전히 아는 인위적 상황의 예제
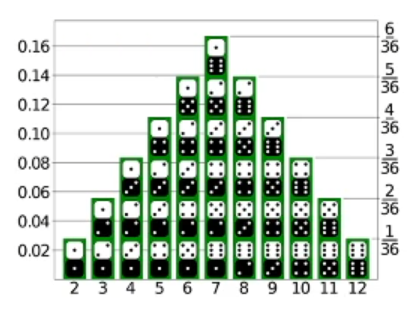
- 예) 두 개 주사위를 던져 나온 눈의 합을 x라 할 때, y=(x-7)2+1 점을 받는 게임
- 이런 상황을 ‘데이터 생성 과정을 완전히 알고 있다’고 말함
- x를 알면 정확히 y를 예측할 수 있음
-> 실제 주사위를 던져 𝕏={3,10,8,5}를 얻었다면, 𝕐={17,10,2,5}
- x의 발생 확률 P(x)를 정확히 알 수 있음
-
P(x)를 알고 있으므로, 새로운 데이터 생성 가능
-
- 예) 두 개 주사위를 던져 나온 눈의 합을 x라 할 때, y=(x-7)2+1 점을 받는 게임
- 위과 같은 실제 기계 학습 문제
- 데이터 생성 과정을 알 수 없음
- 단지 주어진 훈련집합 𝕏, 𝕐로 가설 모델을 통해 근사 추정만 가능
1.3.2 데이터베이스의 중요성
-
데이터베이스의 품질
-
주어진 응용에 맞는 충분히 다양한 데이터를 충분한 양만큼 수집 추정 정확도 높아짐
- 예) 정면 얼굴만 가진 데이터베이스로 학습하고 나면, 기운 얼굴은 매우 낮은 성능
-> 주어진 응용 환경을 자세히 살핀 다음 그에 맞는 데이터베이스 확보는 아주 중요함 -
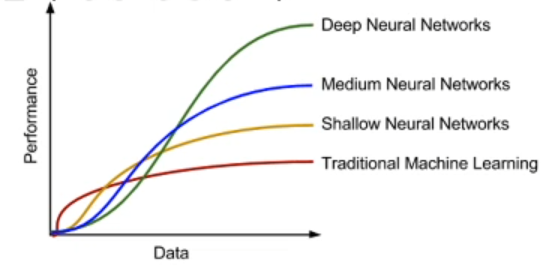
데이터의 양과 학습 모델의 성능 경향성 비교
-
-
공개 데이터베이스
- 기계 학습의 대표적인 3가지 데이터베이스: Iris, MNIST, ImageNet
- UCI 저장소repository리퍼지토리 (2017년11월 기준으로 394개 데이터베이스 제공)
-
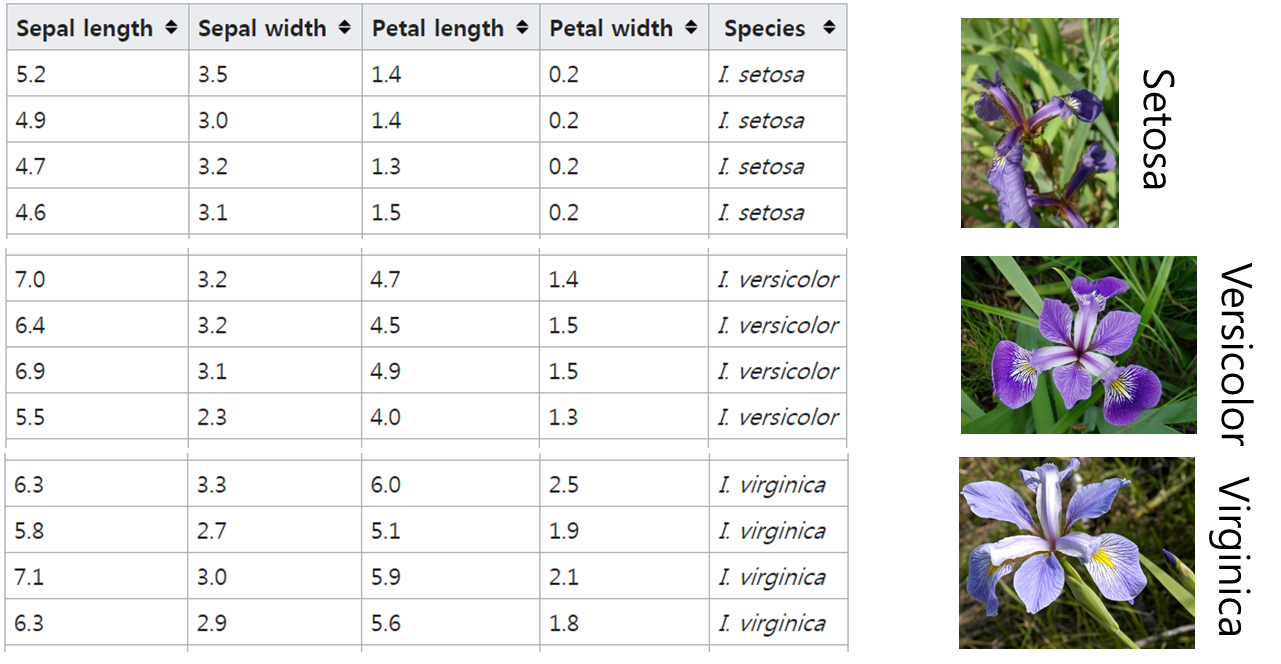
Iris 데이터베이스는 통계학자인 피셔 교수가 1936년에 캐나다 동부 해안의 가스페 반도에 서식하는 3종의 붓꽃(setosa, versicolor, virginica)을 50송이씩 채취하여 만들었다[Fisher1936]. 150개 샘플 각각에 대해 꽃받침 길이, 꽃받침 너비, 꽃잎 길이, 꽃잎 너비를 측정하여 기록하였다. 따라서 4차원 특징 공간이 형성되며 목푯값은 3종을 숫자로 표시함으로써 1, 2, 3 값 중의 하나이다.
-
MNIST 데이터베이스는 미국표준국(NIST)에서 수집한 필기 숫자 데이터베이스로, 훈련집합 60,000자, 테스트집합 10,000자를 제공한다. http://yann.lecun.com/exdb/mnist에 접속하면 무료로 내려받을 수 있으며, 1988년부터 시작한 인식률 경쟁 기록도 볼 수 있다. 2017년 8월 기준으로는 [Ciresan2012] 논문이 0.23%의 오류율로 최고 자리를 차지하고 있다. 테스트집합에 있는 10,000개 샘플에서 단지 23개만 틀린 것이다.

-
ImageNet 데이터베이스는 정보검색 분야에서 만든 WordNet의 단어 계층 분류를 그대로 따랐고, 부류마다 수백에서 수천 개의 영상을 수집하였다[Deng2009]. 총 21,841개 부류에 대해 총 14,197,122개의 영상을 보유하고 있다. 그중에서 1,000개 부류를 뽑아 ILSVRC라는 영상인식 경진대회를 2010년부터 매년 개최하고 있다.

-
데이터의 적은 양 -> 차원의 저주와 관련
- MNIST: 28*28 흑백 비트맵이라면 서로 다른 총 샘플 수는 2784가지이지만, MNIST는 고작 6만 개 샘플
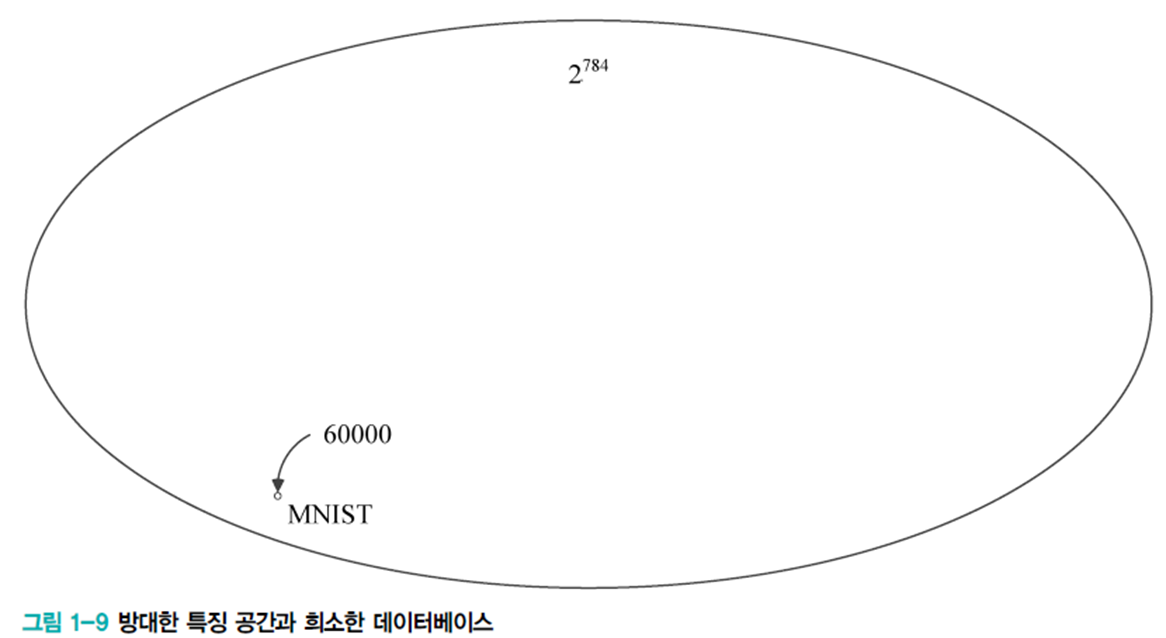
- MNIST: 28*28 흑백 비트맵이라면 서로 다른 총 샘플 수는 2784가지이지만, MNIST는 고작 6만 개 샘플
1.3.3 데이터베이스 크기와 기계 학습 성능
-
적은 양의 데이터베이스로 어떻게 높은 성능을 달성하는가?
-
방대한 공간에서 실제 데이터가 발생하는 곳은 매우 작은 부분 공간임
-> 데이터 희소data sparsity 특성 가정
위와 같은 데이터 발생 확률은 거의 0에 가까움 -
매니폴드(마니 + 끼다) 가정manifold assumption (or manifold hypothesis)
- 고차원의 데이터는 관련된 낮은 차원의 매니폴드에 가깝게 집중되어 있음
- 아래와 같이 일정한 규칙에 따라 매끄럽게 변화
-

1.3.4 데이터 가시화
- 4차원 이상의 초공간은 한꺼번에 가시화 불가능
- 여러 가지 가시화 기법
- 2개씩 조합하여 여러 개의 그래프 그림
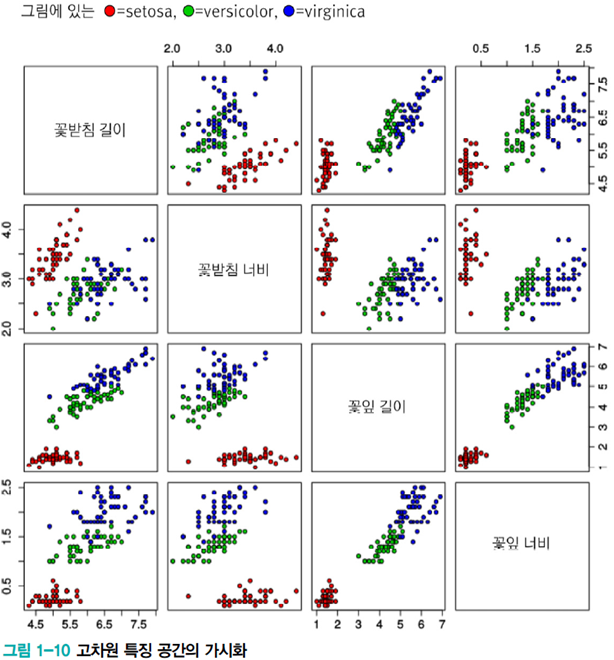
- 2개씩 조합하여 여러 개의 그래프 그림
1.4 간단한 기계 학습의 예
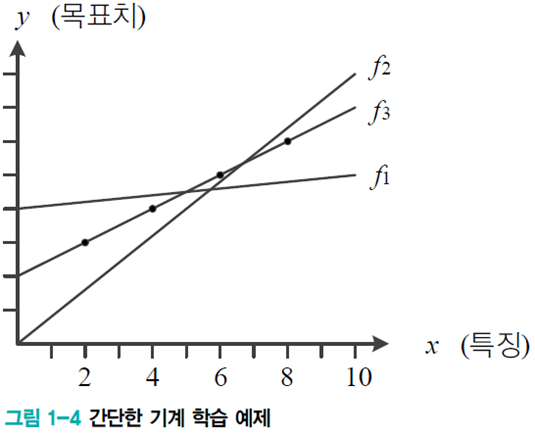
- 선형 회귀linear regression
- [그림 1-4] : 식 (1.2)의 직선 모델(가설)을 사용하므로 두 개의 매개변수 Θ=(𝑤,𝑏)T

- [그림 1-4] : 식 (1.2)의 직선 모델(가설)을 사용하므로 두 개의 매개변수 Θ=(𝑤,𝑏)T
- 목적 함수objective function (또는 비용 함수cost function)
- 식 (1.8)은 선형 회귀를 위한 목적 함수
- 식 (1.8)을 평균제곱오차식MSE(Mean Squared Error)라 부름
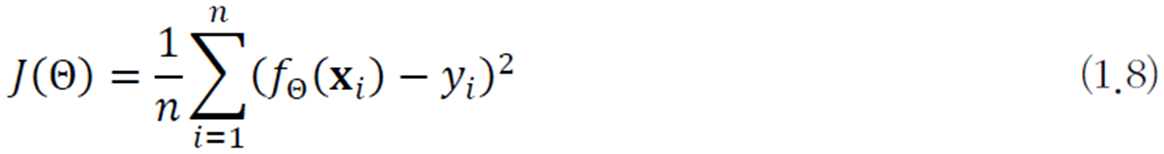
- 𝑓Θ(𝐱i)는 예측함수의 예측 출력, yi는 예측함수가 맞추어야 하는 실제 목표치
- 𝑓Θ(𝐱i) - yi는 오차error 혹은 손실loss
- 식 (1.8)을 평균제곱오차식MSE(Mean Squared Error)라 부름
- 처음에는 최적 매개변수 값을 알 수 없으므로 난수로 Θ1=(𝑤1,b1)T 설정 -> Θ2=(𝑤2,b2)T 로 개선 -> Θ3=(𝑤3,b3)T 로 개선 -> Θ3는 최적해 Θhat
- 𝐽(Θ1)>𝐽(Θ2)> 𝐽(Θ3)
- 식 (1.8)은 선형 회귀를 위한 목적 함수
