Union & Find 알고리즘

1. Union & Find?

해당 알고리즘은 분리되어 있는 두 그룹을 서로 합치는 연산이다.
해당 알고리즘을 사용하면, 사실상 상수 시간에 가까운 속도로 처리할 수 있다.

• Union : 두 그룹을 합치는 연산
• Find : 원소가 속해 있는 그룹을 알아내는 연산

[ Union ]

각 원소의 부모를 관리해주는 배열을 하나 구성한다.
현재는 모든 원소가 부모 정점이 없다는 의미에서 -1로 값을 채워둔다.

그 후, 하나의 원소를 다른 원소의 자식으로 만들어준다.

union(a, b) = a를 b의 부모로 지정한다. = b는 a의 자식이다.

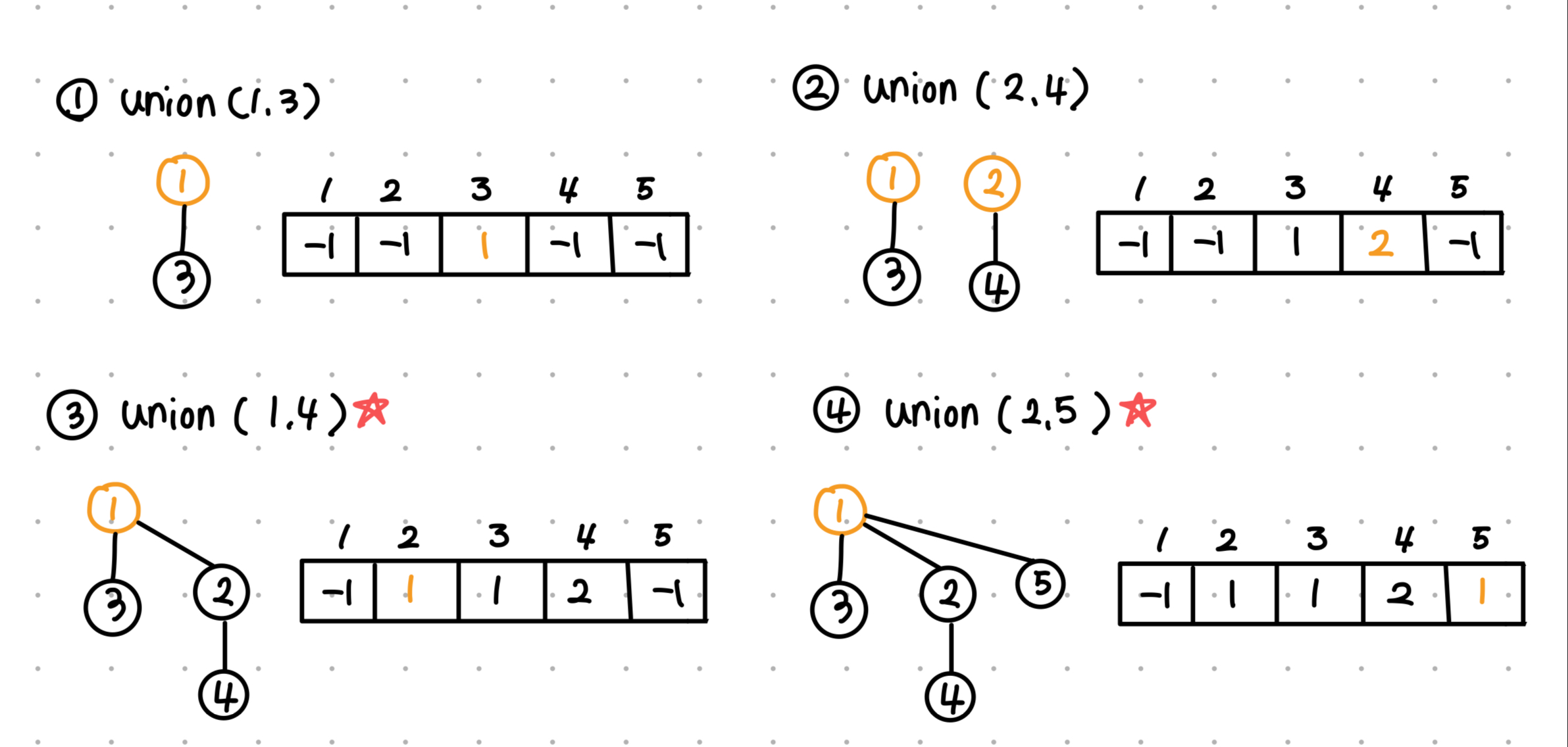
한 가지 주의점은, union(u, v)를 할 때 v의 루트를 u의 루트로 바꿔야 한다!!! 는 점이다.

부모의 원소값이 아닌 루트값임을 기억하자.

[ Find ]

: 그룹 번호가 -1이 되는 원소가 나올 때까지 재귀함수로 타고 올라간다면 끝이다!

---

2. 실제 구현 코드

 int [] p = new int[5];
 Arrays.fill(p, -1);
 ...
 
 int find(int x) {
   while(p[x] > 0) {
      x = p[x];
   }
   return x;
 }
 
 boolean uni(int u, int v) {
    u = find(u);
    v = find(v);
    if(u == v)
       return false;
 
    p[v] = u;
    return true;
 }

---

3. 시간복잡도

find 함수의 실행시간이 전체 실행시간에 큰 영향을 미친다!
즉 정점의 최대 깊이가 O(n)이 될 수도 있음 -> 최적화 필요

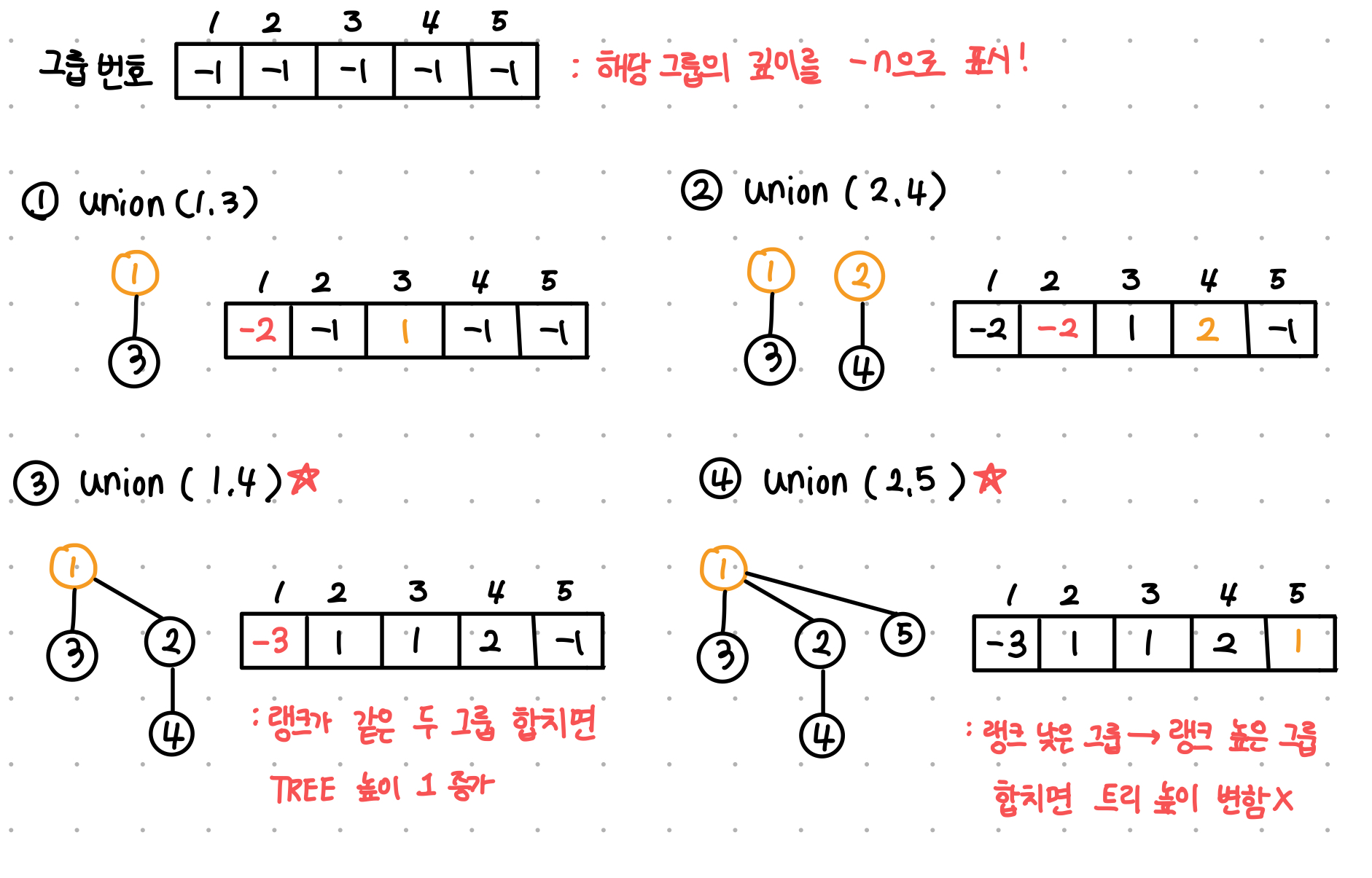
[ Union 최적화] - Union By Rank

정점의 최대 높이를 낮추자!!

루트 노드에 현재 몇 Rank인지 기록하고, 랭크가 높은 그룹을 랭크가 낮은 그룹쪽으로 합쳐주는 전략이다!

구현 코드

boolean uni(int u, int v) {
  u = find(u);
  v = find(v);
  
  if(u==v) return false;
  
  if(p[u] > p[v]) { //자식 그룹의 Rank 더 낮은 상황! 
    swap(u, v) //Rank 낮은게 무조건 부모 자리인 u에 오게 swap
  }
  
  if(p[u] == p[v]) {//랭크가 같은 그룹이 합쳐지면 무조건 tree 높이 1 증가됨
    p[u]--;
  }
  
  p[v] = u;
  return false;
}  
  

[ Find 최적화 ] - 경로 압축

기존 방식은 위에서 설명했듯, 최대 O(n)을 갖게 된다.
즉 각 노드의 경로는 다음과 같을 것이다.

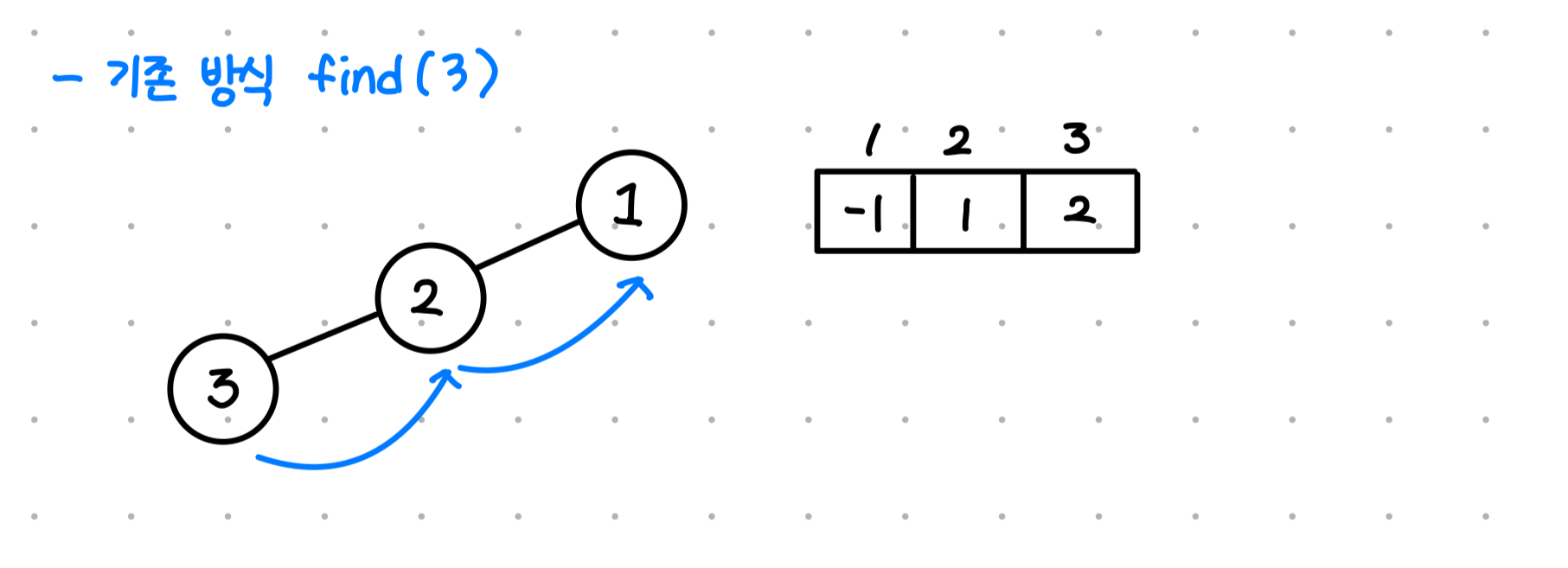
그러나, 노드들이 모두 같은 부모를 바라보게 한다면 어떨까?

이전 방법에서는 3에서 1을 찾기 위해 find 함수를 2번 호출해야 했지만, 이젠 1번의 호출로도 루트가 어디인지 알 수 있다!!

구현 코드

int find(int x) {
  if(p[x] < 0) {
     return x;
  }
  return p[x] = find(p[x]);

3. 최종 구현

int [] p = new int[5];
Arrays.fill(p, -1);
  ...

boolean uni(int u, int v) {
  u = find(u);
  v = find(v);
  
  if(u==v) return false;
  
  if(p[u] > p[v]) { //자식 그룹의 Rank 더 낮은 상황! 
    swap(u, v) //Rank 낮은게 무조건 부모 자리인 u에 오게 swap
  }
  
  if(p[u] == p[v]) {//랭크가 같은 그룹이 합쳐지면 무조건 tree 높이 1 증가됨
    p[u]--;
  }
  
  p[v] = u;
  return false;
}  
  
int find(int x) {
  if(p[x] < 0) {
     return x;
  }
  return p[x] = find(p[x]);
}